Calcular la función de transferencia pulso de los siguientes sistemas en lazo cerrado...
- Primer sistema
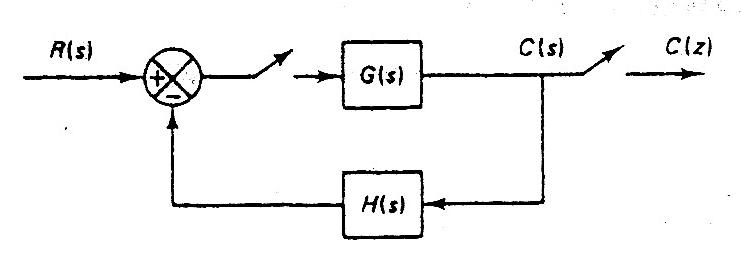
$ \begin{array}{l} Y(s) = E*(s) \cdot G(s) \to Y*(s) = E*(s) \cdot G*(s) \\ E(s) = R(s) - B(s) \to E*(s) = R*(s) - B*(s) \\ B(s) = Y(s) \cdot H(s) \to B*(s) = [Y(s) \cdot H(s)]* \\ ..... \\ E*(s) = R*(s) - B*(s) \\ E*(s) = R*(s) - [Y(s) \cdot H(s)]* \\ E*(s) = R*(s) - [E*(s) \cdot G(s) \cdot H(s)]* \\ E*(s) = R*(s) - E*(s) \cdot [G(s) \cdot H(s)]* \\ E*(s) = R*(s) - E*(s) \cdot GH*(s) \\ E*(s) + E*(s) \cdot GH*(s) = R*(s) \\ E*(s) \cdot [1 + GH*(s)] = R*(s) \\ E*(s) = \dfrac{{R*(s)}}{{1 + GH*(s)}} \\ ..... \\ Y*(s) = E*(s) \cdot G*(s) \\ Y*(s) = \dfrac{{R*(s)}}{{1 + GH*(s)}} \cdot G*(s) \\ Y(z) = \dfrac{{R(z)}}{{1 + GH(z)}} \cdot G(z) \\ \dfrac{{Y(z)}}{{R(z)}} = \dfrac{{G(z)}}{{1 + GH(z)}} \\ \end{array} $
- Segundo sistema
$ \begin{array}{l} E(s) = R(s) - B(s) \to E*(s) = R*(s) - B*(s) \\ Y(s) = E*(s) \cdot G(s) \to Y*(s) = E*(s) \cdot G*(s) \\ B(s) = Y*(s) \cdot H(s) \to B*(s) = Y*(s) \cdot H*(s) \\ ..... \\ E*(s) = R*(s) - B*(s) \\ E*(s) = R*(s) - Y*(s) \cdot H*(s) \\ E*(s) = R*(s) - E*(s) \cdot G*(s) \cdot H*(s) \\ E*(s) + E*(s) \cdot G*(s) \cdot H*(s) = R*(s) \\ E*(s) \cdot [1 + G*(s) \cdot H*(s)] = R*(s) \\ E*(s) = \dfrac{{R*(s)}}{{1 + G*(s) \cdot H*(s)}} \\ ..... \\ Y*(s) = E*(s) \cdot G*(s) \\ Y*(s) = \dfrac{{R*(s)}}{{1 + G*(s) \cdot H*(s)}} \cdot G*(s) \\ Y(z) = \dfrac{{R(z)}}{{1 + G(z) \cdot H(z)}} \cdot G(z) \\ \dfrac{{Y(z)}}{{R(z)}} = \dfrac{{G(z)}}{{1 + G(z) \cdot H(z)}} \\ \end{array} $
- Tercer sistema
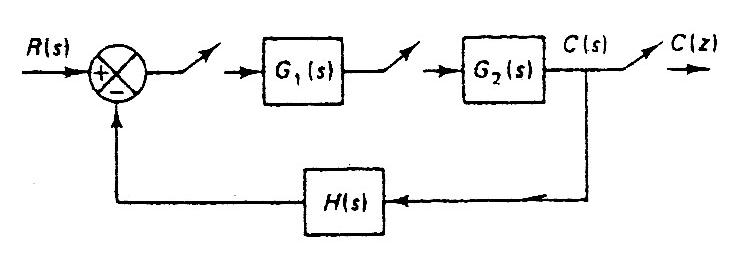
$\begin{array}{l} E(s) = R(s) - B(s) \to E*(s) = R*(s) - B*(s) \\ B(s) = Y(s) \cdot H(s) \to B*(s) = [Y(s) \cdot H(s)]* \\ Y(s) = U*(s) \cdot G_2 (s) \to Y*(s) = U*(s) \cdot G_2 *(s) \\ U(s) = E*(s) \cdot G_1 (s) \to U*(s) = E*(s) \cdot G_1 *(s) \\ \cdots \\ E*(s) = R*(s) - B*(s) \\ E*(s) = R*(s) - [Y(s) \cdot H(s)]*\\ E*(s) = R*(s) - [U*(s) \cdot G_2 (s) \cdot H(s)]* \\ E*(s) = R*(s) - U*(s) \cdot [G_2 (s) \cdot H(s)]* \\ E*(s) = R*(s) - U*(s) \cdot G_2 H*(s) \\ \cdots \\ U*(s) = E*(s) \cdot G_1 *(s) \\ U*(s) = [R*(s) - U*(s) \cdot G_2 H*(s)] \cdot G_1 *(s) \\ U*(s) = R*(s) \cdot G_1 *(s) - U*(s) \cdot G_2 H*(s) \cdot G_1 *(s) \\ U*(s) + U*(s) \cdot G_2 H*(s) \cdot G_1*(s) = R*(s) \cdot G_1 *(s) \\ U*(s) \cdot [1 + G_2 H*(s) \cdot G_1*(s)] = R*(s) \cdot G_1 *(s) \\ U*(s) = \dfrac{R*(s) \cdot G_1 *(s)}{1 +G_2 H*(s) \cdot G_1 *(s)} \\ \cdots \\ Y*(s) = U*(s) \cdot G_2 *(s) \\ \end{array}$
$\begin{array}{l}Y*(s) = \left[ \dfrac{R*(s) \cdot G_1 *(s)}{1 + G_2 H*(s) \cdot G_1 *(s)} \right] \cdot G_2 *(s) \\ Y*(s) = \dfrac{{R*(s) \cdot G_1 *(s) \cdot G_2 *(s)}}{{1 + G_2 H*(s) \cdot G_1 *(s)}} \\ Y(z) = \dfrac{{R(z) \cdot G_1 (z) \cdot G_2 (z)}}{{1 + G_2 H(z) \cdot G_1 (z)}} \\ \dfrac{{Y(z)}}{{R(z)}} = \dfrac{{G_1 (z) \cdot G_2 (z)}}{{1 + G_2 H(z) \cdot G_1 (z)}}\end{array}$
Contenidos licenciados bajo Creative Commons by-sa 3.0
