Cálculo de la Función de Transferencia Pulso de varios sistemas en lazo cerrado

Calcular la función de transferencia pulso de los siguientes sistemas en lazo cerrado...

- Primer sistema

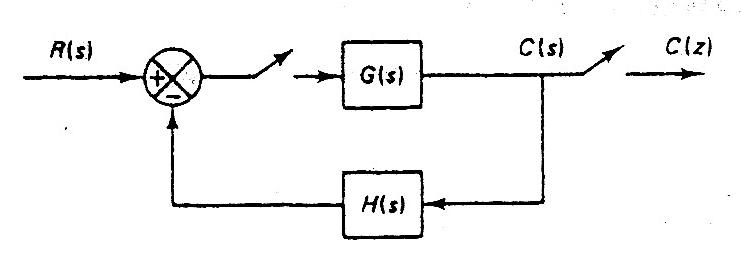
$ \begin{array}{l} Y(s) = E*(s) \cdot G(s) \to Y*(s) = E*(s) \cdot G*(s) \\ E(s) = R(s) - B(s) \to E*(s) = R*(s) - B*(s) \\ B(s) = Y(s) \cdot H(s) \to B*(s) = [Y(s) \cdot H(s)]* \\ ..... \\ E*(s) = R*(s) - B*(s) \\ E*(s) = R*(s) - [Y(s) \cdot H(s)]* \\ E*(s) = R*(s) - [E*(s) \cdot G(s) \cdot H(s)]* \\ E*(s) = R*(s) - E*(s) \cdot [G(s) \cdot H(s)]* \\ E*(s) = R*(s) - E*(s) \cdot GH*(s) \\ E*(s) + E*(s) \cdot GH*(s) = R*(s) \\ E*(s) \cdot [1 + GH*(s)] = R*(s) \\ E*(s) = \dfrac{{R*(s)}}{{1 + GH*(s)}} \\ ..... \\ Y*(s) = E*(s) \cdot G*(s) \\ Y*(s) = \dfrac{{R*(s)}}{{1 + GH*(s)}} \cdot G*(s) \\ Y(z) = \dfrac{{R(z)}}{{1 + GH(z)}} \cdot G(z) \\ \dfrac{{Y(z)}}{{R(z)}} = \dfrac{{G(z)}}{{1 + GH(z)}} \\ \end{array} $

- Segundo sistema

$ \begin{array}{l} E(s) = R(s) - B(s) \to E*(s) = R*(s) - B*(s) \\ Y(s) = E*(s) \cdot G(s) \to Y*(s) = E*(s) \cdot G*(s) \\ B(s) = Y*(s) \cdot H(s) \to B*(s) = Y*(s) \cdot H*(s) \\ ..... \\ E*(s) = R*(s) - B*(s) \\ E*(s) = R*(s) - Y*(s) \cdot H*(s) \\ E*(s) = R*(s) - E*(s) \cdot G*(s) \cdot H*(s) \\ E*(s) + E*(s) \cdot G*(s) \cdot H*(s) = R*(s) \\ E*(s) \cdot [1 + G*(s) \cdot H*(s)] = R*(s) \\ E*(s) = \dfrac{{R*(s)}}{{1 + G*(s) \cdot H*(s)}} \\ ..... \\ Y*(s) = E*(s) \cdot G*(s) \\ Y*(s) = \dfrac{{R*(s)}}{{1 + G*(s) \cdot H*(s)}} \cdot G*(s) \\ Y(z) = \dfrac{{R(z)}}{{1 + G(z) \cdot H(z)}} \cdot G(z) \\ \dfrac{{Y(z)}}{{R(z)}} = \dfrac{{G(z)}}{{1 + G(z) \cdot H(z)}} \\ \end{array} $

- Tercer sistema

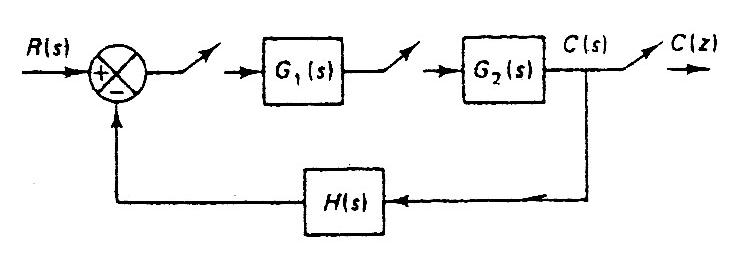
$\begin{array}{l} E(s) = R(s) - B(s) \to E*(s) = R*(s) - B*(s) \\ B(s) = Y(s) \cdot H(s) \to B*(s) = [Y(s) \cdot H(s)]* \\ Y(s) = U*(s) \cdot G_2 (s) \to Y*(s) = U*(s) \cdot G_2 *(s) \\ U(s) = E*(s) \cdot G_1 (s) \to U*(s) = E*(s) \cdot G_1 *(s) \\ \cdots \\ E*(s) = R*(s) - B*(s) \\ E*(s) = R*(s) - [Y(s) \cdot H(s)]*\\ E*(s) = R*(s) - [U*(s) \cdot G_2 (s) \cdot H(s)]* \\ E*(s) = R*(s) - U*(s) \cdot [G_2 (s) \cdot H(s)]* \\ E*(s) = R*(s) - U*(s) \cdot G_2 H*(s) \\ \cdots \\ U*(s) = E*(s) \cdot G_1 *(s) \\ U*(s) = [R*(s) - U*(s) \cdot G_2 H*(s)] \cdot G_1 *(s) \\ U*(s) = R*(s) \cdot G_1 *(s) - U*(s) \cdot G_2 H*(s) \cdot G_1 *(s) \\ U*(s) + U*(s) \cdot G_2 H*(s) \cdot G_1*(s) = R*(s) \cdot G_1 *(s) \\ U*(s) \cdot [1 + G_2 H*(s) \cdot G_1*(s)] = R*(s) \cdot G_1 *(s) \\ U*(s) = \dfrac{R*(s) \cdot G_1 *(s)}{1 +G_2 H*(s) \cdot G_1 *(s)} \\ \cdots \\ Y*(s) = U*(s) \cdot G_2 *(s) \\ \end{array}$

$\begin{array}{l}Y*(s) = \left[ \dfrac{R*(s) \cdot G_1 *(s)}{1 + G_2 H*(s) \cdot G_1 *(s)} \right] \cdot G_2 *(s) \\ Y*(s) = \dfrac{{R*(s) \cdot G_1 *(s) \cdot G_2 *(s)}}{{1 + G_2 H*(s) \cdot G_1 *(s)}} \\ Y(z) = \dfrac{{R(z) \cdot G_1 (z) \cdot G_2 (z)}}{{1 + G_2 H(z) \cdot G_1 (z)}} \\ \dfrac{{Y(z)}}{{R(z)}} = \dfrac{{G_1 (z) \cdot G_2 (z)}}{{1 + G_2 H(z) \cdot G_1 (z)}}\end{array}$

Ejercicio 1 F.T.P (enviado para casa)

El esquema del problema es el siguiente:

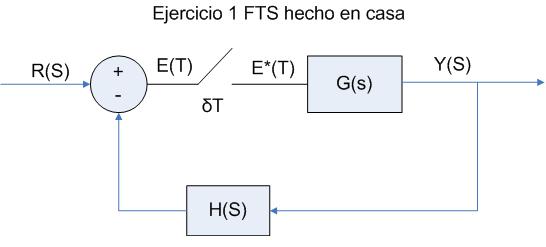
Como necesitamos la salida muestreada tenemos que colocar un muestreador imaginario al final del esquema, quedando de la siguiente forma:

Del cual sacamos las siguientes ecuaciones:

$1.$ $Y(s)=G(s)E^*(s)$

$2.$ $B(s)=H(s)Y(s)$

$3.$ $E(s)=R(s)-B(s)$

Y queremos obtener la funcion de transferencia pulso:

$\dfrac{Y(z)}{R(z)} \rightarrow \dfrac{Y^*(s)}{R^*(s)} $

Para ello resolvemos el sistema utilizando todas las ecuaciones:

1. $E(s)=R(s)-B(s)\rightarrow E^*(s)=[R(s)-B(s)]^*= R^*(s)-B^*(s)= R^*(s)-[Y(s)H(s)]^*=$

$R^*-[G(s)E^*(s)H(s)]^*=R^*-E(s)^*[G(s)H(s)]^* \rightarrow E^*(s)=\dfrac{R(s)}{1+GH^*(s)}$

Nótese que $GH^*(s)$ es $[G(s)H(s)]^*$.

2. $Y(s)=G(s)E^*(s) \rightarrow Y^*(s)=[G(s)E^*(s)]^*=E^*(s)G^*(s)$

Por lo tanto tenemos que nuestra funcion de transferencia pulso queda de la forma:

$Y^*(s)=\dfrac{R^*(s)}{1+GH^*(s)}G^*(s) \rightarrow \dfrac{Y^*(s)}{R^*(s)} = \dfrac{G^*(s)}{1+GH^*(s)}$

Ejercicio 2 F.T.P (hecho en clase)

El esquema es el siguiente:

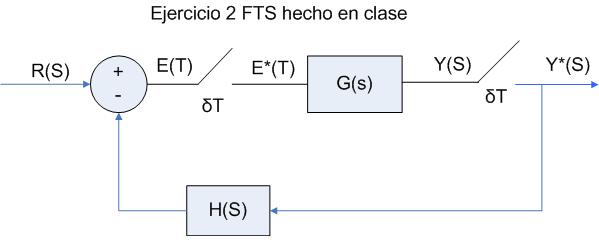
En este caso tenemos un muestreador con lo cual no nos hace falta porque obtenemos directamente Y*(s):

Las ecuaciones son las siguientes:

1. $E(s)=R(s)-B(s)$

2.$B(s)=H(s)Y^*(s)$ de estas dos primeras obtenemos $E(s)=R(s)-H(s)Y^*(s) \rightarrow E^*(s)=R^*(s)-H^*(s)Y^*(s)$

3.$Y(s)=G(s)E^*(s) \rightarrow Y^*(s)=E^*(s)G^*(s) \rightarrow Y^*(s)=R^*(s)G^*(s)-H^*(s)G^*(s)Y^*(s) $

$\rightarrow Y(s)^*[1+G^*(s)H^*(s)]=R^*(s)G^*(s)$

Finalmente, transformamos el sistema a dominio Z, sacamos factor comun Y^*(s):

$\dfrac{Y(z)}{R(z)}=\dfrac{G(z)}{1+G(z)H(z)}$

Ejercicio 4 F.T.P. (Enviado para casa)

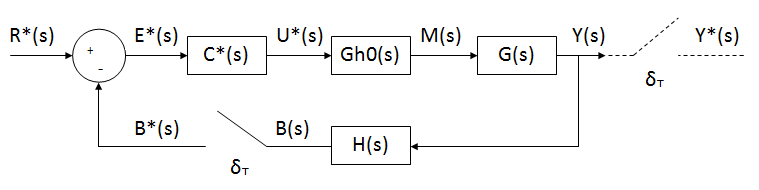
Ecuaciones del sistema:

$1. $ $E^*(s)=R^*(s)-B^*(s)$

$2.$ $U^*(s)=E^*(s)C^*(s)$

$3.$ $M(s)=Gh0(s)U^*(s)$

$4.$ $Y(s)=M(s)G(s)$

$5.$ $B(s)=Y(s)H(s)$

Vamos a obtener $E^*(s)$:

$E^*(s)=R^*(s)-B^*(s)=R^*(s)-[Y(s)H(s)]^*=R^*(s)-[M(s)G(s)H(s)]^*=R^*(s)-[Gh0(s)U^*(s)G(s)H(s)]^*$

$E^*(s)=R*(s)-U^*(s)*[Gh0(s)G(s)H(s)]^*=R^*(s)-E^*(s)C^*(s)[Gh0(s)G(s)H(s)]^*$

$E^*(s)=\dfrac{R^*(s)}{1+C^*(s)*[Gh0(s)G(s)H(s)]^*}$

Desarrollamos $Y(s)$ hasta llegar a una expresión que contenga $E^*(s)$:

$Y(s)=M(s)G(s)=Gh0(s)U^*(s)G(s)=E^*(s)C^*(s)Gh0(s)G(s)$

$Y(s)=\dfrac{C^*(s)Gh0(s)G(s)R^*(s)}{1+C^*(s)*[Gh0(s)G(s)H(s)]^*}$

$Y^*(s)=\dfrac{C^*(s)R^*(s)*[Gh0(s)G(s)]^*}{1+C^*(s)*[Gh0(s)G(s)H(s)]^*}$

$\dfrac{Y^*(s)}{R^*(s)}=\dfrac{C^*(s)*[Gh0(s)G(s)]^*}{1+C^*(s)*[Gh0(s)G(s)H(s)]^*}$

Realizamos el cambio $Gh0(s)=\dfrac{1-e^{-Ts}}{s}$

$\dfrac{Y^*(s)}{R^*(s)}=\dfrac{C^*(s)*[\dfrac{1-e^{-Ts}}{s}G(s)]^*}{1+C^*(s)*[\dfrac{1-e^{-Ts}}{s}G(s)H(s)]^*}$

$1-e^{-Ts}$ está muestrado y se representa como $F^*(s)$

$\dfrac{Y^*(s)}{R^*(s)}=\dfrac{C^*(s)F^*(s)*[\dfrac{G(s)}{s}]^*}{1+C^*(s)F^*(s)*[\dfrac{G(s)H(s)}{s}]^*}$

Aplicamos transformada Z, teniendo en cuenta:

$F^*(s)=1-e^{-Ts}$ y $z=e^{Ts}$

$\dfrac{Y(z)}{R(z)}=\dfrac{C(z)F(z)*Z\lbrace\dfrac{G(s)}{s}\rbrace}{1+C(z)F(z)*Z\lbrace\dfrac{G(s)H(s)}{s}\rbrace}=\dfrac{C(z)(1-z^{-1})*G_1(z)}{1+C(z)(1-z^{-1})*G_1H(z)}$, siendo $G_1(s) = \dfrac{G(s)}{s}$.