La utilización de un esquema realimentado en un sistema de control suele ser vital pra que la estrategia de control tenga éxito. Los efectos de la realimentación influyen en muchos aspectos del comportamiento del sistema: respuesta estática, respuesta dinámica, respuesta frente a perturbaciones, sensibilidad a la variación de parámetros del sistema, etc.
Para analizar y para diseñar sistemas de control, es necesario tener una base de comparación del desempeño del sistema de control. Esa base se configura especificando señales de prueba particulares, y comprobando las respuestas de distintos tipos de sistemas frente a estas entradas.
Las señales de prueba que se utilizan regularmente son la entrada impulsiva, escalón, rampa, parábola y senoidal. Con estas señales es posible realizar con facilidad análisis matemáticos y experimentales de los sistemas de control, ya que son funciones simples; además, estas señales permiten estudiar distintas características de las respuestas estáticas y dinámicas de los sistemas de control.
La forma de las señales de referencia a las que el sistema vaya a estar sujeto en su funcionamiento cotidiano, determinará el tipo de entrada que se debe utilizar para el análisis.
La utilización de estas señales de prueba permite comparar la respuesta de distintos sistema de control frente a las mismas señales. También es muy importante para la elección de las señales de prueba saber qué tipo de análisis se desea realizar, por ejemplo, se utilizará una señal escalon para estudiar el error de estado estacionario de posición de un sistema, y nomalmente también para estudiar su dinámica, sin embargo, se empleará una señal senoidal si se desea estudiar la respuesta en frecuencia del mismo.
Para estudiar matemáticamente el comportamiento de los sistemas dinámicos es importante que las ecuaciones no se compliquen en exceso. Por esto es muy común suponer que los sistemas tienen un número pequeño de polos y ceros. En muchas ocasiones es necesario realizar simplificaciones del sistema basadas en las constantes de tiempo de sus polos y ceros, de forma que se obtenga una representación simplificada del mismo que facilite su análisis. Cuando se está frente a un problema de diseño, una de las posibles estrategias es anular polos y ceros de la planta mediante el controlador con la idea de tener una dinámica en lazo cerrado más sencilla que facilite dicho diseño.
En los sistemas con 1 ó 2 polos dominantes es relativamente sencillo relacionar la localización de sus polos con la respuesta dinámica del sistema, por lo que son estos sistemas los tipos clásicos empleados como referencias a la hora de enfrentarse a un proceso de diseño.
Ejercicio error
Se desea diseñar el sistema de control de la figura, para que cumpla las siguientes especificaciones:
a) Error de estado estacionario menor del 10%, para una entrada rampa y 0 para una entrada escalón.
b) Sobre impulso máximo, menor del 5%.
c) Tiempo de asentamiento (2%), menor de 3 seg.
d) Dibujar sobre el plano “S” la región donde puedan estar ubicados los polos del sistema, para que se cumplan las especificaciones.
ess(2%)≤10%
Mp≤5%
ts(2%)≤3seg
Si tiene sobre impulso, es porque es un sistema subamortiguado. Por lo tanto:
\[G_{(s)}=\frac{K_o·{\omega n}^2}{s^2+2\delta \omega ns+{\omega n}^2}\]
Hallamos su función de transferencia:
\[G_{\left(s\right)}=\frac{Y(s)}{R(s)}=\]
\[\frac{K_1·\frac{1}{s\left(s+2\right)}}{1+K_1·\frac{1}{s\left(s+2\right)}·\left(1+K_2s\right)}=\]
\[\frac{\frac{K_1}{s\left(s+2\right)}}{\frac{s\left(s+2\right)+K_1\left(1+K_2s\right)}{s\left(s+2\right)}}=\]
\[\frac{K_1}{s\left(s+2\right)+K_1\left(1+K_2s\right)}=\]
\[\frac{K_1}{s^2+2s+K_1+K_1K_2s}=\]
\[\frac{K_1}{s^2+(2+K_1K_2)s+K_1}=\]
Comparando la primera ecuación y la última podemos obtener:
NOTA: Sólo en casos muy concretos será posible comparar la función de transferencia del sistema con la de un sistema de 2º orden. En los casos donde la comparación no sea posible, será necesario realizar el Lugar Geométrico de las Raíces y escoger unos polos de lazo cerrado que permitan el cumplimiento de las especificaciones.
\[K_1={\omega n}^2·Ko\]
\[2+K_1K_2=2\delta \omega n\]
\[{\omega n}^2=K_1\]
Por lo tanto:
\[\omega n=\sqrt{K_1}\]
\[Ko=1\]
\[2\delta \omega n=2+K_1K_2\ \to \ \]
\[\delta =\frac{2+K_1K_2}{2\omega n}\ \to \]
\[\delta =\frac{2+K_1K_2}{2\sqrt{K_1}}\]
A continuación despejamos la señal de error:
\[E_{(s)}=R_{(s)}-M_{(s)}\]
\[M_{(s)}=Y_{\left(s\right)}(1+K_2s)\]
\[Y_{(s)}=\frac{U_{(s)}}{s(s+2)}\]
\[U_{(s)}=E_{(s)}·K_1\]
\[E_{(s)}=R_{(s)}-\frac{E_{(s)}·K_1}{s(s+2)}(1+K_2s)\]
\[E_{(s)}+\frac{E_{(s)}·K_1}{s(s+2)}(1+K_2s)=R_{(s)}\]
\[E_{\left(s\right)}(1+\frac{K_1}{s\left(s+2\right)}\left(1+K_2s\right))=R_{(s)}\]
\[E_{\left(s\right)}=\frac{R_{(s)}}{1+\frac{K_1}{s(s+2)}(1+K_2s)}\]
Aplicamos El teorema del valor final: (para la señal de error $E_{(s)}$)
\[R_{(s)}=\frac{1}{s^2}\]
\[e_{ss}={\mathop{\lim }_{s\to 0} s·\ }E_{(s)}=\]
\[{\mathop{\lim }_{s\to 0} s·\ }\frac{R_{(s)}}{1+\frac{K_1}{s(s+2)}(1+K_2s)}=\]
\[{\mathop{\lim }_{s\to 0} s·\ }\frac{1}{s^2}\frac{1}{1+\frac{K_1(1+K_2s)}{s(s+2)}}=\]
\[{\mathop{\lim }_{s\to 0} \frac{1}{s+\frac{{sK}_1(1+K_2s)}{s(s+2)}}=\ }\]
\[\frac{1}{0+\frac{K_1+K_1K_20}{0+2}}=\frac{1}{\frac{K_1}{2}}=\frac{2}{K_1}\]
Igualamos las ecuaciones del error para despejar K1:
\[e_{ss}\le 10\%=0.1\]
\[0.1\ge \frac{2}{K_1}\ \ \to \ \ K_1\ge 20\]
Igualamos las ecuaciones del sobreimpulso para calcular el delta:
\[Mp=e^{\frac{-\delta ·\pi }{\sqrt{1-{\delta }^2}}}\]
\[Mp\le 5\%=0.05\]
\[0.05=e^{\frac{-\delta ·\pi }{\sqrt{1-{\delta }^2}}}\ \ \ \to \ \ \ \ \ \]
\[{(ln\ 0.05)}^2={\left(\frac{-\delta ·\pi }{\sqrt{1-{\delta }^2}}\right)}^2\ \ \to \]
\[8.97=\frac{-\delta ·\pi }{1-{\delta }^2}\ \ \ \to \]
[8.97-8.97·{\delta }^2={\delta }^2{\pi }^2\ \ \ \to \ \ \ \ \ \ \]
[8.97={\delta }^2·{\pi }^2+8.97{\delta }^2\ \ \ \to \]
\[\frac{8.97}{{\pi }^2+8.97}={\delta }^2\]
\[\delta =\sqrt{\frac{8.97}{{\pi }^2+8.97}}\ \ \ \to \ \ \ \delta \ge 0.69\]
Igualamos las ecuaciones del tiempo de asentamiento:
\[{ts}_{\left(2\%\right)}\le 3seg.\]
\[{ts}_{\left(2\%\right)}=\frac{4}{\delta \omega n}\]
\[\frac{4}{\delta \omega n}\le 3\ \ \ \to \ \ \ 4\le 3\delta \omega n\ \ \ \to \ \ \ \frac{4}{3}\le \delta \omega n\]
\[\omega n=\sqrt{K_1}\]
\[K_1\ge 20\]
\[0.69·\sqrt{20}=3.086\ \ \ \to \ \ \ 3.086\ge 3\]
Igualamos las ecuaciones para calcular K2:
\[\delta =\frac{2+K_1K_2}{2\sqrt{K_1}}\ \ \ \to \ \ \ \ \ \]
\[2+K_1K_2\ge 2\sqrt{K_1}·0.69\ \ \ \to \]
\[K_2\ge \frac{2·\sqrt{K_1}·0.69-2}{K_1}\]
\[K_1=20\]
\[\delta =0.69\]
\[K_2\ge \frac{2·\sqrt{20}·0.69-2}{20}\ \ \ \to \ \ \ K_2\ge 0.2086\]
Como $K_1\ge 20$, le damos por ejemplo el valor de 30:
Igualamos las ecuaciones para calcular delta:
\[K_2=0.2086\]
\[K_1=30\]
\[K_2\ge \frac{2·\sqrt{K_1}·\delta -2}{K_1}\ \ \ \to \ \ \ \]
\[\ \ \frac{K_2·K_1+2}{2·\sqrt{K_1}}\ge \delta \ \ \ \to \]
\[\frac{0.2086·30+2}{2·\sqrt{30}}\ge \delta \ \ \ \to \ \ \ \delta \le 0.75\]
Igualamos las ecuaciones para calcular el sobreimpulso:
\[Mp=e^{\frac{-\delta ·\pi }{\sqrt{1-{\delta }^2}}}\ \ \ \to \ \ \]
\[Mp=e^{\frac{-0.75·\pi }{\sqrt{1-{0.75}^2}}}\ \ \ \ \to \ \ \ Mp=0.028=2.8\%\]
\[\delta \le 0.75\]
Igualamos ecuaciones para calcular el error:
\[e_{ss}=\frac{2}{K_1}\ \ \ \ \to \ \ \ e_{ss}=\frac{2}{30}\ \ \ \to \ \ \ e_{ss}=0.067=6.7\%\]
\[K_1=30\]
Igualamos ecuaciones para calcular el tiempo de asentamiento:
\[{ts}_{\left(2\%\right)}=\frac{4}{\delta \omega n}\ \ \ \to \ \ \ {ts}_{\left(2\%\right)}=\frac{4}{0.75·\sqrt{30}}\ \ \ \to \ \ \ {ts}_{\left(2\%\right)}=0.97seg.\]
\[\omega n=\sqrt{K_1}=\sqrt{30}\]
\[\delta \le 0.75\]
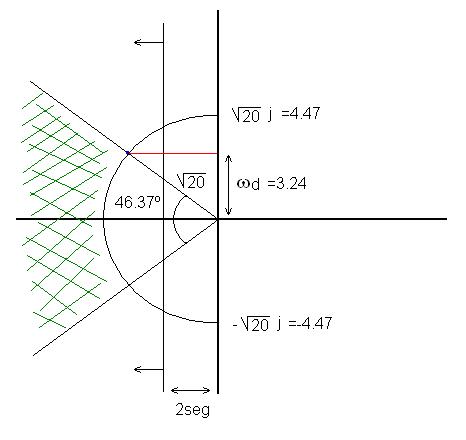
Ahora vamos a dibujar la gráfica con los datos que tenemos:
\[\beta =arcos\ \delta \ \ \ \to \ \ \ \beta =arcos\ 0.69=46.37º\]
\[\omega d=\sqrt{20}·\sqrt{1-{0.69}^2}\ \ \ \ \to \ \ \ \omega d=4.47·0.7238=3.24\ \ \ \to \ \ \ \sigma =\delta \omega n=\]
\[0.69·\sqrt{20}=3.086\]
Ejercicio error real
Se desea diseñar el sistema de control de la figura, para que cumpla las siguientes especificaciones:
a) Error de estado estacionario menor del 10%, para una entrada rampa y 0 para una entrada escalón.
b) Sobre impulso máximo, menor del 5%.
c) Tiempo de asentamiento (2%), menor de 3 seg.
d) Dibujar sobre el plano “S” la región donde puedan estar ubicados los polos del sistema, para que se cumplan las especificaciones.
Para calcular el error real ($E_{\left(S\right)}=R_{(S)}-Y_{(S)}$):
ess(/)≤10%
Mp≤5%
ts(2%)≤3seg
Si tiene sobre impulso, es porque es un sistema subamortiguado. Por lo tanto:
\[G_{(S)}=\frac{K_o·{\omega n}^2}{S^2+2\delta \omega nS+{\omega n}^2}\]
Hallamos su función de transferencia:
\[G_{\left(S\right)}=\frac{Y(s)}{R(s)}=\]
\[\frac{K_1·\frac{1}{S\left(S+2\right)}}{1+K_1·\frac{1}{s\left(s+2\right)}·\left(1+K_2S\right)}=\]
\[\frac{\frac{K_1}{S\left(S+2\right)}}{\frac{S\left(S+2\right)+K_1\left(1+K_2S\right)}{S\left(S+2\right)}}=\]
\[\frac{K_1}{S\left(S+2\right)+K_1\left(1+K_2S\right)}=\]
\[=\frac{K_1}{S^2+2S+K_1+K_1K_2S}=\]
\[\frac{K_1}{S^2+(2+K_1K_2)S+K_1}\]
\[Y_{(S)}=R_{(S)}·\frac{K_1}{S^2+(2+K_1K_2)S+K_1}\]
Comparando la primera ecuación y la última podemos obtener:
NOTA: Sólo en casos muy concretos será posible comparar la función de transferencia del sistema con la de un sistema de 2º orden. En los casos donde la comparación no sea posible, será necesario realizar el Lugar Geométrico de las Raíces y escoger unos polos de lazo cerrado que permitan el cumplimiento de las especificaciones.
\[K_1={\omega n}^2·Ko\]
\[2+K_1K_2=2\delta \omega n\]
\[{\omega n}^2=K_1\]
Por lo tanto:
\[\omega n=\sqrt{K_1}\]
\[Ko=1\]
\[2\delta \omega n=2+K_1K_2\ \to \ \]
\[\delta =\frac{2+K_1K_2}{2\omega n}\ \to \]
\[\delta =\frac{2+K_1K_2}{2\sqrt{K_1}}\]
A continuación despejamos la señal de error:
Realizamos, ($E_{\left(S\right)}=R_{(S)}-Y_{(S)}$):
\[Y_{(S)}=R_{(S)}·\frac{K_1}{S^2+(2+K_1K_2)S+K_1}\]
\[E_{(S)}=R_{(S)}-Y_{(S)}\ \ \ \to \ \ \ \]
\[E_{(S)}=R_{(S)}-\left(R_{(S)}·\frac{K_1}{S^2+(2+K_1K_2)S+K_1}\right)\]
\[E_{(S)}=R_{(S)}\left(1-\frac{K_1}{S^2+(2+K_1K_2)S+K_1}\right)\ \ \ \to \ \ \ \]
\[E_{(S)}=R_{(S)}\left(\frac{S^2+\left(2+K_1K_2\right)S+K_1-K_1}{S^2+(2+K_1K_2)S+K_1}\right)\ \to\ \]
\[E_{(S)}=R_{(S)}\left(\frac{S^2+\left(2+K_1K_2\right)S}{S^2+(2+K_1K_2)S+K_1}\right)\]
Aplicamos El teorema del valor final: (para la señal de error $E_{\left(S\right)}$)
\[R_{(S)}=\frac{1}{S^2}\]
\[e_{SS}={\mathop{\lim }_{S\to 0} S·\ }E_{(S)}={\mathop{\lim }_{S\to 0} S·\ }R_{(S)}\left(\frac{S^2+\left(2+K_1K_2\right)S}{S^2+(2+K_1K_2)S+K_1}\right)=\]
\[{\mathop{\lim }_{S\to 0} S·\ }\frac{1}{S^2}·\frac{S^2+\left(2+K_1K_2\right)S}{S^2+(2+K_1K_2)S+K_1}=\]
\[{\mathop{\lim }_{S\to 0}\ \frac{S+\left(2+K_1K_2\right)}{S^2+(2+K_1K_2)S+K_1}=\ }\]
\[\frac{0+\left(2+K_1K_2\right)}{0+(2+K_1K_2)0+K_1}=\]
\[\frac{0+\left(2+K_1K_2\right)}{0+0+K_1}=\]
\[\frac{2+K_1K_2}{K_1}=\]
\[\frac{2}{K_1}+K_2\]
Igualamos con el error:
\[e_{SS}\le 10\%=0.1\]
\[e_{SS}=\frac{2}{K_1}+K_2\]
\[\frac{2}{K_1}+K_2<0.1\]
\[\frac{2}{K_1}<0.1-K_2\ \ \ \to \ \ \ K_1>\frac{2}{0.1-K_2}\]
\[0.1-\frac{2}{K_1}>K_2\ \ \ \to \ \ \ K_2<0.1-\frac{2}{K_1}\]
Calculamos el delta:
\[Mp=e^{\frac{-\delta ·\pi }{\sqrt{1-{\delta }^2}}}\]
\[Mp\le 5\%=0.05\]
\[0.05=e^{\frac{-\delta ·\pi }{\sqrt{1-{\delta }^2}}}\ \ \ \to \ \ \ \]
\[{(ln\ 0.05)}^2={\left(\frac{-\delta ·\pi }{\sqrt{1-{\delta }^2}}\right)}^2\ \ \to \]
\[8.97=\frac{-\delta ·\pi }{1-{\delta }^2}\ \ \ \to \]
\[8.97-8.97·{\delta }^2={\delta }^2{\pi }^2\ \ \ \to \ \ \ \ \ \ \]
\[8.97={\delta }^2·{\pi }^2+8.97{\delta }^2\ \ \ \to \]
\[\frac{8.97}{{\pi }^2+8.97}={\delta }^2\]
\[\delta =\sqrt{\frac{8.97}{{\pi }^2+8.97}}\ \ \ \to \ \ \ \delta \ge 0.69\]
Igualamos las ecuaciones del tiempo de asentamiento:
\[{ts}_{\left(2\%\right)}\le 3seg.\]
\[{ts}_{\left(2\%\right)}=\frac{4}{\delta \omega n}\]
\[\frac{4}{\delta \omega n}\le 3\ \ \ \to \ \ \ 4\le 3\delta \omega n\ \ \ \to \ \ \ \frac{4}{3}\le \delta \omega n\]
Igualamos las ecuaciones del delta:
\[\delta =\frac{2+K_1K_2}{2\sqrt{K_1}}\ \ \ \to \ \]
\[\delta =0.69\]
\[\frac{2+K_1K_2}{2\sqrt{K_1}}>0.69\ \ \ \to \]
\[K_2>\frac{2·\sqrt{K_1}·0.69-2}{K_1}\]
Igualamos las ecuaciones para despejar K2:
\[\frac{4}{3}\le \delta \omega n\]
\[\omega n=\sqrt{K_1}\]
\[\delta =\frac{2+K_1K_2}{2\sqrt{K_1}}\]
\[\frac{4}{3}\le \frac{2+K_1K_2}{2\sqrt{K_1}}·\sqrt{K_1}\ \ \ \ \to \]
\[\frac{\frac{4}{3}·2-2}{K_1}\le K_2\ \ \ \to \]
\[\frac{\frac{8}{3}-2}{K_1}\le K_2\ \ \ \to \]
\[\frac{\frac{8-6}{3}}{K_1}\le K_2\ \ \ \to \]
\[\frac{\frac{2}{3}}{K_1}\le K_2\ \ \ \to \ \ \ K_2\ge \frac{2}{3·K_1}\]
Para un valor de $K_1$ los límites de $K_2$ serían:
Límite inferior: Sobreimpulso
\[K_2>\frac{2·\sqrt{K_1}·0.69-2}{K_1}\]
Tiempo de asentamiento
\[K_2>\frac{2}{3·K_1}\]
Límite superior:
Error
\[K_2<0.1-\frac{2}{K_1}\]
A continuación, se pone el código de programación en matlab, en el cual se representan los límites de para un rango de valores de . Dado un valor de , se calcula como el valor intermedio a los límites. Si no se cumplen los requisitos se vuelve a pedir un valor de .
Clc, clear all, close all
%Representar límites de K2 en función de K1
K1=100:0.1:300;
K2min1=(2*0.69*sqrt(K1)-2)./K1;
K2min2=2./(3*K1);
K2min=max(K2min1,K2min2);
K2max=0.1-2./K1;
Plot(K1,K2min1,ylabel(‘K2’),grid on
%Escoger un valor de K2
K2min=inf;K2max=0;K2=0;
While (K2<K2min || K2>K2max)
K1=input(‘Escoge un valor correcto para K1:’);
%Uno cercano al límite para cumplir las especificaciones es K1=195
%También se puede hacer con ‘ginput’ gráficamente
%K1=ginput(1);K1=K1(1);
K2min1=(2*0.69*sqrt(K1)-2)./K1;
K2min2=2/(3*K1);
K2min=max(K2min1,K2min2);
K2max=0.1-2./K1;
K2=K2min+(K2max-K2min)/2;
End
%Representa el punto escogido en la gráfica
Hold on,plot(K1,K2,’r+’)
%Mostrar los valores escogidos
K1,K2
%Obtener el sistema realimentado ya diseñado
G=K1*tf(1,[1,2,0]);
H=tf([K2,1],1);
S=feedback(G,H);
%Simular frente a una entrada escalón
Figure,step(S)
Title(‘entrada escalon’)
Xlabel(‘tiempo (S)’), ylabel(‘y(t)’)
&Simular frente a una entrada rampa
T=0:0.1:1;
R=t;
Figure, [y,t]=lsim(S,r,t);
Plot(t,t, ‘r - -’,t,y)
Title(‘entrada rampa’)
Xlabel(‘tiempo (S)’),ylabel(‘y(t)’)
%Calcular el error con matlab
Error_teorico=K2+2/K1
Error_real=t(end)-y(end)
PROBLEMA PROPUESTO:
Sacar la función de transferencia y estudiar los distintos sistemas de segundo orden en función del factor de amortiguamiento del siguiente circuito:
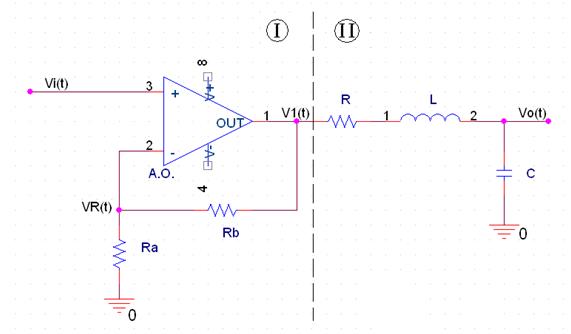
Ht(s) = H1 (s) * H2(s)
Etapa (I) Amplificador no inversor, esta etapa es la encargada de introducir ganancia en el circuito.
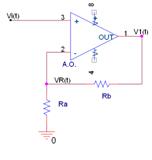
$H1(t) = \frac{{V1(t)}}{{Vi(t)}} = 1 + \frac{{Rb}}{{Ra}}$ ---> ${\rm{VR(t) = }}\frac{{{\rm{Ra}}}}{{{\rm{Ra + Rb}}}}V1(t)$
Vi(t)=VR(t)
${\rm{Vi(t) = }}\frac{{{\rm{Ra}}}}{{{\rm{Ra + Rb}}}}V1(t)$ ---> ${\rm{H1(s) = }}\frac{{V1(s)}}{{Vi(s)}} = \frac{{{\rm{Ra}}}}{{{\rm{Ra + Rb}}}} = 1 + \frac{{Rb}}{{Ra}}$
Etapa (II),circuito RLC:
-------> 
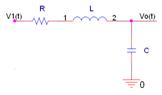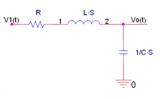
${\rm{H2(s) = }}\frac{{Vo(s)}}{{V1(s)}}$ ----> $Vo(s) = \frac{{\frac{1}{{Cs}}}}{{R + Ls + \frac{1}{{Cs}}}}V1(s)$
$Vo(s) = \frac{{\frac{1}{{Cs}}}}{{\frac{{CRs+CLs^2+1}}{{Cs}}}}V1(s)$ ----> $Vo(s) = \frac{1}{{CRs+CLs^2+1}}V1(s)$
$Vo(s) = \frac{{\frac{1}{{LC}}}}{{\frac{{Rs}}{L}+s^2+\frac{1}{{LC}}}}V1(s) $ -----> $Vo(s) = \frac{{\frac{1}{{LC}}}}{{s^2+\frac{{Rs}}{L}+\frac{1}{{LC}}}}V1(s)$
Etapa (I) y etapa (II): H t(s) = H1(s) * H2(s)
$Ht(s) = \frac{{V1(s)}}{{V1(s)}}\frac{{{\rm{Vo(s)}}}}{{{\rm{V1(s)}}}} = (\frac{{Ra}}{{Ra+Rb}})\frac{{\frac{1}{{LC}}}}{{\frac{{Rs}}{L}+s^2+\frac{{1}}{{LC}}}}$
Función transferencia de 2º orden:
$Ht(s) = \frac{{\frac{1}{{LC}}(1+\frac{{Rb}}{{Ra}})}}{{\frac{{Rs}}{L}+s^2+\frac{1}{{LC}}}}$ ------> $\approx Ht(s) =\frac{{Ko \cdot Wn^2}}{{s^2+2\cdot\delta\cdot Wn \cdot s+Wn^2 }}$
$Wn = \frac{1}{{\sqrt {LC} }}$
$ 2 \cdot \delta \cdot Wn = \frac{R}{L}\Rightarrow \delta= \frac{{\frac{R}{L}}}{{\frac{2}{{\sqrt {LC} }}}} = \frac{R}{2}\sqrt{\frac{C}{L}}$
Coeficiente de amortiguamiento: $\delta= \frac{R}{2}\sqrt{\frac{C}{L}} $
· Sistema Sobreamortiguado: $\delta > 1$ ----> $\delta=\frac{R}{2}\sqrt{\frac{C}{L}}> 1$
· Sistema Críticamente amortiguado: $\delta = 1$ ----> $\delta= \frac{R}{2}\sqrt{\frac{C}{L}} = 1$
· Sistema Subamortiguado: $ 0 < \delta < 1$ ----> $ 0 < \delta = \frac{R}{2}\sqrt{\frac{C}{L}} < 1$
Contenidos licenciados bajo Creative Commons by-sa 3.0
