

En este libro se crearán los apuntes relacionados con la asignatura Control por computador.
Introducción, tipos de señales, Sistemas LTI, ...
Utilización de la transformada $\mathbf{Z}$ y $\mathbf{Z^{-1}}$ para la resolución de ecuaciones en direncia.
Utilización de la descomposición en Fracciones simples para el cálculo de $\mathbf{Z^{-1}}$.
a) Resolver la siguiente ecuación en diferencias, siendo u(k) una entrada impulsiva (delta de Kronecker [1]):
$y(k)=0.5 y(k-1) - 0.25 y(k-3) - u(k) -1.5 u(k-1) + 2 u(k-2)$
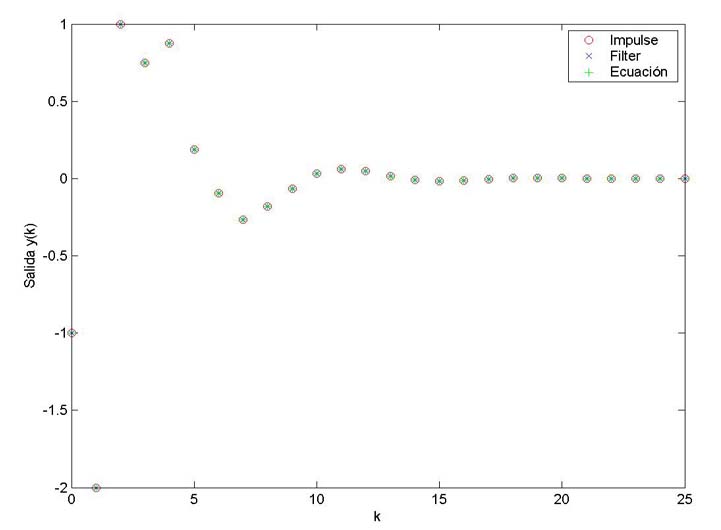
b) Obtener $y(k)$ mediante la simulación de la ecuación en diferencia (comando filter), mediante la función de transferencia (comando impulse) y mediante la resolución de la ecuación en diferencias (programando la solución de dicha ecuación).
c) Calcular $y(\infty)$ mediante el teorema del valor final y comprobar con la solución obtenida en el apartado anterior, haciendo $\lim_{ k \rightarrow \infty} \; y(k)$, que es resultado es correcto.
Resolución del apartado a):
Haciendo la transformada $\mathbf{Z}$ a la ecuación en diferencias anterior, obtenemos:
$Y(z)=0.5 z^{-1} Y(z) - 0.25 z^{-3} Y(z) - U(z) - 1.5 z^{-1} U(z) + 2 z^{-2}U(z)$
$Y(z) (1 - 0.5 z^{-1} + 0.25 z^{-3}) = U(z) (-1 - 1.5 z^{-1} + 2 z^{-2})$
$Y(z)=\dfrac{(-1 - 1.5 z^{-1} + 2 z^{-2})}{(1 - 0.5 z^{-1} + 0.25 z^{-3})} U(z)$
Como $u(k) = \delta (k)$ tenemos que $U(z) = 1$. Por lo tanto:
$ Y(z) = \dfrac{(-1 - 1.5 z^{-1} + 2 z^{-2})}{(1 - 0.5 z^{-1} + 0.25 z^{-3})} = \dfrac{-z^3-1.5z^2+2z}{z^3-0.5z^2+0.25}$
Para obtener $y(k)$ debemos calcular $\mathbf{Z^{-1}}\left \{ Y(z) \right \}$, para ello empezaremos obteniendo la descomposición en fracciones simples de $\dfrac{Y(z)}{z}$.
Las raices de la expresión $1 - 0.5 z^{-1} + 0.25 z^{-3} = 0$ son: $\left \{ \begin{array}{l}z = 0.5 +- 0.5j \\ z = 0.5\end{array} \right.$
$\dfrac{Y(z)}{z} = \dfrac{-z^2-1.5z^1+2}{z^3-0.5z^2+0.25} = \dfrac{A}{(z+0.5)} + \dfrac {Bz+C}{(z-0.5-0.5j)(z-0.5+0.5j)} = \dfrac{A}{(z+0.5)} + \dfrac {Bz+C}{(z-0.5)^2 + {0.5}^2}$
Como A es el residuo de una raiz real simple, podemos calcularlo como:
$\left. A = \dfrac{(-z^2-1.5z^1+2)}{(z+0.5)((z-0.5)^2 + {0.5}^2)}(z+0.5) \right | _ {z=-0.5} = \dfrac {-(-0.5)^2-1.5 (-0.5)+2}{(-0.5-0.5)^2+{0.5}^2}= 2$
Para calcular B y C podemos sumar la expresión $\dfrac{Y(z)}{z}$ y compararla con la original:
$\dfrac{Y(z)}{z} = \dfrac{A(z^2-z+0.5)+(Bz+C)(z+0.5)}{(z+0.5)((z-0.5)^2 + {0.5}^2)} = \dfrac{A(z^2-z+0.5)+Bz^2+0.5Bz+Cz+0.5C}{z^3-0.5z^2+0.25}$
Como los denominadores son idénticos (debe ser siempre así), comparamos los numeradores:
${-z^2-1.5z^1+2} = z^2(A+B) + z (-A+0.5B+C) + 0.5(A+C)$
Comparando término a término, debe cumplirse:
$\begin{array}{rcl}-1 &=& A+B \\ -A+0.5B+C &=& -1.5 \\ 0.5(A+C)&=&2 \end{array}$
Tenemos 3 ecuaciones con 3 incógnitas, por lo que podemos resolver A, B y C. Como A ya lo hemos calculado antes, A=2, podemos obtener B y C despejando:
$ B= -1-A = -1 -2 = -3$
$C= \dfrac {2-0.5A}{0.2} = \dfrac {2-0.5 \cdot 2}{0.2} = 2$
Se puede comprobar que $-A+0.5B+C = -2+0.5 \cdot (-3) + 2 = 1.5$
Por lo tanto,
$\dfrac {Y(z)}{z} = \dfrac{2}{(z+0.5)} + \dfrac {-3z+2}{(z-0.5)^2 + {0.5}^2} \Rightarrow Y(z) = \dfrac{2z}{(z+0.5)} + \dfrac {-3z^2+2z}{(z-0.5)^2 + {0.5}^2}$
La descomposición en fracciones simples también puede realizarse mediante el comando residue de MATLAB. Para ello tecleamos:
B=[-1,-1.5,2]; A=[1,-0.5,0,0.25]; % Polinomios numerador y denominador de Y(z)/z
[R,P,K]=residue(B,A)
Que nos retorna:
R =
-1.5 - 0.5i
-1.5 + 0.5i
2
P =
0.5 + 0.5i
0.5 - 0.5i
-0.5
K =
[]
Por lo tanto la descomposición en fracciones simples es:
$\dfrac {Y(z)}{z} = \dfrac {(-1.5-0.5i)}{(z-0.5-0.5j)} + \dfrac{(-1.5+0.5i)}{(z-0.5+0.5j)} + \dfrac{2}{(z+0.5)}$
Las dos primeras fracciones tienen residuos y polos complejos, con lo que no nos servirán para aplicar las tablas de transformadas. Para corregir esto debemos realizar la suma de dichas fracciones. Podemos hacerlo con MATLAB:
num = R(1)*[1,-P(2)]+R(2)*[1,-P(1)]
Cuyo resultado es [3,2], esto es, $3z+2$.
El denominador podemos hacerlo como "suma por diferencia, diferencia de cuadrados":
$(z-0.5-0.5j)(z-0.5+0.5j) = (z-0.5)^2 + {0.5}^2$
Es decir, obtenemos exactamente la misma expresión que antes:
$\dfrac {Y(z)}{z} = \dfrac{2}{(z+0.5)} + \dfrac {-3z+2}{(z-0.5)^2 + {0.5}^2} \Rightarrow Y(z) = \dfrac{2z}{(z+0.5)} + \dfrac {-3z^2+2z}{(z-0.5)^2 + {0.5}^2}$
Una vez descompuesta Y(z) en fracciones simples, podemos buscar cada una de estas en las tablas de transformadas para realizar la transformada $\mathbf{Z^{-1}}$:
$\mathbf{Z^{-1}}\left \{ \dfrac{2}{(z+0.5)} \right \} = 2(-0.5)^k$
Para obtener $\mathbf{Z^{-1}}\left \{ \dfrac{-3z^2+2z}{(z-0.5)^2+0.5^2} \right \}$ debemos realizar algunas operaciones previamente:
Si la parte real del polo es $\sigma = -0.5$, y la parate imaginaria $\omega = 0.5$,
el módulo es $c = \sqrt {\sigma ^2 + \omega ^2} = \sqrt {(-0.5)^2 + 0.5^2} = sqrt{0.5}$.
$sen(b) = \omega / c = 0.5 / \sqrt{0.5} = \sqrt{0.5}$,
$cos(b) = \sigma / c = 0.5 / \sqrt{0.5} = \sqrt{0.5}$
$b = arccos(\sqrt{0.5})$
Necesitamos obtener un numeradr igual a $z^2 -c \cdot z \cdot cos(b) = z^2 - \sqrt{0.5} \cdot z \cdot \sqrt{0.5} = z^2 -0.5 z$ para obtener una expresión de la forma $c^k\; cos(bk)$, y un numerador igual a $c \cdot z \cdot sen(b) = \sqrt{0.5} \cdot z \cdot \sqrt{0.5} = 0.5 z$ para obtener una expresión de la forma $c^k\; sen(bk)$.
$\mathbf{Z^{-1}}\left \{ \dfrac{-3z^2+2z}{(z-0.5)^2+0.5^2} \right \} = (-3) \mathbf{Z^{-1}}\left \{\dfrac{z^2-\dfrac {2}{3}z}{(z-0.5)^2+0.5^2} \right \} = (-3) \mathbf{Z^{-1}}\left \{\dfrac{z^2 -0.5z+0.5z-\dfrac {2}{3}z}{(z-0.5)^2+0.5^2} \right \} =$
$= -3 \mathbf{Z^{-1}}\left \{\dfrac{z^2 -0.5z}{(z-0.5)^2+0.5^2} \right \}+ \mathbf{Z^{-1}}\left \{ \dfrac{0.5z}{(z-0.5)^2+0.5^2}\right \}$
Ya tenemos las 2 expresiones buscadas, con lo que podemos calcular la transformada $\mathbf{Z^{-1}}$de cada una de ellas:
$-3 \mathbf{Z^{-1}}\left \{\dfrac{z^2 -0.5z}{(z-0.5)^2+0.5^2} \right \} = (-3)\sqrt{0.5}^k\; cos(bk)$
$\mathbf{Z^{-1}}\left \{ \dfrac{0.5z}{(z-0.5)^2+0.5^2}\right \} = \sqrt{0.5}^k\; sen (bk)$
Con este paso ya hemos concluido y podemos poner la expresión definitiva de y(k):
$y(k) = 2 (-0.5)^k + 0.5^{k/2} \left ( sen(bk)-3cos(bk) \right )$, siendo $b = arccos(\sqrt{0.5})$.
Resolución del apartado b):
En primer lugar vamos a realizar la simulación creando la funcíón de transferencia mediante el comando de Matlab "tf".
El comando tf crea una función de transferencia con los exponentes positivos a partir de los coeficientes que acopañan a Z en el numerador y el denominador.
La función de transferencia ya la tenemos calculada anteriormente:
$ G(z) =\dfrac{-z^3-1.5z^2+2z}{z^3-0.5z^2+0.25}$
Por lo que los coeficientes del numerador y denominador quedarían así:
Numerador --> [-1, 1.5, 2, 0]
Denominador-->[1, -0.5, 0, 0.25]
La función tf necesita un tercer parámetro que se corresponde con el periodo de muestreo. En nuestro caso no tendremos periodo de muestreo y lo indicaremos con un vector vacio [] como tercer parámetro.
La función quedaría de la siguiente forma:
G= tf([-1, 1.5, 2, 0], [1, -0.5, 0, 0.25], []);
Para simular esta función con una entrad impulso usamos el comando de Matlab "impulse", al que pasamos la función G como parámetro.
[y1,k]= impulse(G);
y1 contendrá la salida del sistema tras aplicarle la función impulso como entrada.
k tiene un vector de coordenadas en el eje X con una serie de valores que da Matlab para ajustar la gráfica de una forma correcta.
A continuación realizaremos la misma simulación con el comando "filter"
El comando Filter de Matlab se utiliza para crear secuencias de ponderación. Sus tres parámetros son el vector A de constantes que acompañan a las Y(k), el vector B de constantes que acompañan a las U(k) y un tercer vector como entrada al sistema.
En nuestro caso el vector de entrada será una delta de Kronecker. Para simularla crearemos un vector con todas las componentes a cero excepto la primera, simulando el comportamiento de la delta.
[1 0 0 0 0 0 0 0 0 0 0 .....]
Para ajustar el tamaño del vector en todas las representaciones utilizaremos el vector k obtenido con tf.
delta=zeros(size(k));
delta(1)=1;
A continuación creamos los vectores con los coeficientes, tomándolos directamente de la ecuación en diferencias después de agrupar las Y(k) y U(k) a un lado y a otro de la igualdad:
$$y(k)-0.5 y(k-1) +0.25 y(k-3) =- u(k) -1.5 u(k-1) + 2 u(k-2)$$
B=[-1, -1.5, 2];
A=[1, -0.5, 0, 0.25]
Para simular capturamos en y2 los valores de la salida del sistema.
y2=filter(B,A,delta);
La tercera simulación la realizamos con la ecuación obtenida en el apartado A de forma manual.
b=arcos(sqrt(0.5));
y3=2*(-0.5).^k+0.5.^(k/2).*(-3*cos(b*k)+sin(b*k));
Instrucciones en Matlab
%funcion de transferencia
G=tf([-1, -1.5, 2, 0],[1,-0.5,0,0.25],[]);
[y1,k]=impulse(G);
%funcion en diferencias
delta=zeros(size(k));delta(1)=1;
B=[-1,-1.5,2];
A=[1,-0.5,0,0.25];
y2=filter(B,A,delta);
%funcion calculada
b=acos(sqrt(0.5));
y3=2*(-0.5).^k+0.5.^(k/2).*(-3*cos(b*k)+sin(b*k));
plot(k,y1,'ro');
hold on
plot(k,y2,'bx');
plot(k,y3,'g+');
xlabel('k'),ylabel('Salida y(k)')
legend('Impulse','Filter','Ecuación')
Resolución del apartado c):
Haciendo el límite a y(k) obtenida en el apartado a) tenemos:
$\lim_ {k \rightarrow \infty}\, y(k) = \lim_ {k \rightarrow \infty} \, 2(-0.5)^k + 0.5^{k/2} \left ( sen(bk)-3cos(bk) \right ) = 0.$
Es 0 porque tanto $0.5^k$ como $0.5^{k/2}$ tienden a 0 al aumentar k, y la expresión formada por el seno y el coseno está acotada.
Aplicando el Teorema del Valor Final:
$y(\infty) = \lim_ {z \rightarrow 1} {\dfrac {(z-1)}{z}\, Y(z)} = \lim_ {z \rightarrow 1} \, \dfrac {(z-1)}{z} \, \dfrac{(-z^3-1.5z^2+2z)}{(z^3-0.5z^2+0.25)} = \dfrac{0 (-1-1.5+2)}{1 (1-0.5+0.25)} = 0$
Como es lógico se obtiene el mismo resultado que además coincide con el de la simulación.
a) Resolver la siguiente ecuación en diferencias, siendo u(k) una entrada escalon (u(k)={1,1,1...}):
$y(k)=0.5 y(k-1)-0.12 y(k-2) +0.008 y(k-3) +u(k-2) +2 u(k-3)$
b) Obtener $y(k)$ mediante la simulación de la ecuación en diferencia (comando filter), mediante la función de transferencia (comando step) y mediante la resolución de la ecuación en diferencias (programando la solución de dicha ecuación).
c) Calcular $y(\infty)$ mediante el teorema del valor final y comprobar con la solución obtenida en el apartado anterior, haciendo $\lim_{ k \rightarrow \infty} \; y(k)$, que es resultado es correcto.
Resolución del apartado a):
Haciendo la transformada $\mathbf{Z}$ a la ecuación en diferencias anterior, obtenemos:
$Y(z)=0.5 z^{-1} Y(z) - 0.12 z^{-2} Y(z) + 0.008 z^{-3} Y(z) + U(z)z^{-2} + 2 U(z)z^{-3}$
$Y(z) (1 - 0.5 z^{-1} +0.12z^{-2} -0.008z^{-3}) = U(z) (z^{-2} + 2 z^{-3})$
$Y(z)=\dfrac{(z^{-2}+ 2 z^{-3})}{(1 - 0.5 z^{-1} + 0.12 z^{-2} -0.008z^{-3})} U(z)$
Como $u(k) =\{1,1,1,..\} $ tenemos que $U(z) = \dfrac{(z)}{(z-1)}$. Por lo tanto:
$ Y(z) = [\dfrac{(z^{-2}+ 2 z^{-3})}{(1 - 0.5 z^{-1} + 0.12 z^{-2} -0.008z^{-3})}. \dfrac{z^3}{z^3}] \dfrac{z}{(z-1)} = \dfrac{-z+2}{z^3-0.5z^2+0.12z-0.008} . \dfrac{z}{(z-1)}$
- Notas: Solo se ha multiplicado el primer termino por $\dfrac{z^3}{z^3}$ para pasar los exponentes a positivos, y no se ha efectuado la operación con $\dfrac{z}{(z-1)}$ con la idea de utilizar la z del numerador para el $\dfrac{Y(z)}{z}$ que veremos a continuación y el denominador como polo ya resuelto del sistema (asi ya tenemos calculado uno).
Para obtener $y(k)$ debemos calcular $\mathbf{Z^{-1}}\left \{ Y(z) \right \}$, para ello empezaremos obteniendo la descomposición en fracciones simples de $\dfrac{Y(z)}{z}$.
Las raices de la expresión $z^3 -0.5z^2 +0.12z -0.008 = 0$ son: $\left \{ \begin{array}{l}z = 0.2 +- 0.2j \\ z = 0.2\end{array} \right.$
$\dfrac{Y(z)}{z} = \dfrac{z+2}{(z-1)(z^3 -0.5z^2 +0.12Z -0.008)} = \dfrac{A}{(z-1)} + \dfrac {Bz+C}{(z-0.2-0.2j)(z-0.2+0.2j)} + \dfrac {D}{z-0.1} = \dfrac{A}{(z-1)} + \dfrac {Bz+C}{(z-0.2)^2 + {0.2}^2} + \dfrac{D}{z-0.1}$
Como A es el residuo de una raiz real simple, podemos calcularlo como:
$\left. A = \dfrac{(z+2)}{(z-1)((z-0.2)^2 + {0.2}^2)(z-0.1)}(z-1) \right | _ {z=1} = \dfrac {3}{((1-0.2)^2+{0.2}^2)(0.9)}\simeq 4.9$
Con D pasa lo mismo, asi que lo calculamos de la siguiente manera también:
$\left. D = \dfrac{(z+2)}{(z-1)((z-0.2)^2 + {0.2}^2)(z-0.1)}(z-0.1) \right | _ {z=0.1} = \dfrac {2.1}{(-0.9)((0.1-0.2)^2+{0.2}^2)}\simeq 46.6$
Para calcular B y C podemos sumar la expresión $\dfrac{Y(z)}{z}$ y compararla con la original:
$\dfrac{Y(z)}{z} = \dfrac{A((z-0-2)^2 + 0.2^2)(z-0.1) + (Bz+C)(z-1)(z-0.1) + D((z-0.2)^2+0.2^2)(z-1)}{(z-1)((z-0.2)^2+0.2^2)(z-0.1)}$
Comparando término a término, debe cumplirse:
$\begin{array}{rcl}A+B+D &=&0\\ -0.5A-1.1B+C-0.6D &=& 0 \\ 0.12A + 0.1B - 1.1C + 0.48D&=&1 \\-0.08A + 0.1C -0.08D &=&2 \end{array}$
De la ultima sacamos C
$ 1.1C=2-0.04*46.6-0.008*4.9$
$C= \dfrac{2 -3.73 -0.0392}{0.1} =-17.69$
Con C deberiamos obtener de las otras ecuaciones que:
$D=41.93 $
Por lo tanto,
$\dfrac {Y(z)}{z} \simeq \dfrac{4.9}{(z-1)} + \dfrac {42z-17}{(z-0.2)^2 + {0.2}^2} + \dfrac{46.6}{z-0.1}\Rightarrow Y(z) \simeq \dfrac{4.9z}{(z-1)} + \dfrac {42z^2-17z}{(z-0.2)^2 + {0.2}^2} + \dfrac{46.6z}{z-0.1}$
*La descomposición en fracciones simples también puede realizarse mediante el comando residue de MATLAB. Para ello tecleamos:
B=[1,2]; A=conv([1,-0.5,0.12,-0.008],[1,-1]); % Polinomios numerador y denominador de Y(z)/z
[R,P,K]=residue(B,A)
Que nos retorna:
R =
4.9020
20.8824 + 21.4706i
20.8824 - 21.4706i
46.6667
P =
1
0.2 + 0.2i
0.2 - 0.2i
0.1
K =
[]
Por lo tanto la descomposición en fracciones simples es:
$\dfrac {Y(z)}{z} = \dfrac {(4.9020)}{(z-1)} + \dfrac{(20.8824+21.4706j)}{(z-(0.2+0.2j))} + \dfrac{(20.8824-21.4706j)}{(z-(0.2-0.2j))} + \dfrac{46.6667}{z-0.1}$
Las dos primeras fracciones tienen residuos y polos complejos, con lo que no nos servirán para aplicar las tablas de transformadas. Para corregir esto debemos realizar la suma de dichas fracciones. Podemos hacerlo con MATLAB:
num = R(2)*[1,-P(3)]+R(3)*[1,-P(2)]
Cuyo resultado es [41.7647,-16.9411], esto es, $41.7647z-16.9411$.
El denominador podemos hacerlo como "suma por diferencia, diferencia de cuadrados":
$(z-0.2-0.2j)(z-0.2+0.2j) = (z-0.2)^2 + {0.2}^2$
den = conv([1,-P(2),[1,-P(3)]) =[1,-0.4,0.08]
Es decir, obtenemos exactamente la misma expresión que antes:
$\dfrac {Y(z)}{z} = \dfrac{4.9020}{(z-1)} + \dfrac {41.7647z-16.9411}{(z-0.2)^2 + {0.2}^2} + \dfrac{-46.6667}{z-0.1} \Rightarrow Y(z) = \dfrac{4.9020z}{(z-1)} + \dfrac {41.7647z^2-16.9411z}{(z-0.2)^2 + {0.2}^2} + \dfrac{-46.6667z}{z-0.1}$
Una vez descompuesta Y(z) en fracciones simples, podemos buscar cada una de estas en las tablas de transformadas para realizar la transformada $\mathbf{Z^{-1}}$:
$\mathbf{Z^{-1}}\left \{ \dfrac{4.902z}{(z-1)} \right \} = 4.902(1)^k$
$\mathbf{Z^{-1}}\left \{ \dfrac{-46.6667z}{(z-0.1)} \right \} = -46.6667(0.1)^k$
Para obtener $\mathbf{Z^{-1}}\left \{ \dfrac{41.7647z^2 - 16.9411z}{(z-0.2)^2+0.2^2} \right \}$ debemos realizar algunas operaciones previamente:
Si la parte real del polo es $\sigma = 0.2$, y la parate imaginaria $\omega = 0.2$,
el módulo es $c = \sqrt {\sigma ^2 + \omega ^2} = \sqrt {(0.2)^2 + 0.2^2} = sqrt{0.08}$.
$sen(b) = \omega / c = 0.2 / \sqrt{0.5} = 2.5\sqrt{0.08}$,
$cos(b) = \sigma / c = 0.2 / \sqrt{0.2} = 2.5\sqrt{0.08}$
$b = arccos(\sqrt{0.08})$
Necesitamos obtener un numeradr igual a $z^2 -c \cdot z \cdot cos(b) = z^2 -\sqrt{0.08} \cdot z \cdot 2.5\sqrt{0.08} = z^2 -0.2 z$ para obtener una expresión de la forma $c^k\; cos(bk)$, y un numerador igual a $c \cdot z \cdot sen(b) = \sqrt{0.08} \cdot z \cdot2.5 \sqrt{0.08} = 0.2 z$ para obtener una expresión de la forma $c^k\; sen(bk)$.
$\mathbf{Z^{-1}}\left \{ \dfrac{41.7647z^2 - 16.9411z}{(z-0.2)^2+0.2^2} \right \}\simeq \mathbf{Z^{-1}}\left \{\dfrac{42z^2-17z}{(z-0.2)^2+0.2^2} \right \} =(42) \mathbf{Z^{-1}}\left \{\dfrac{z^2-0.4z}{(z-0.2)^2+0.2^2} \right \} =$
$= (42) \mathbf{Z^{-1}}\left \{\dfrac{z^2 -0.2z -0.2z }{(z-0.2)^2+0.2^2} \right \}= (42) \mathbf{Z^{-1}}\left \{\dfrac{z^2 -0.2z }{(z-0.2)^2+0.2^2} \right \}-(42) \mathbf{Z^{-1}}\left \{\dfrac{0.2z }{(z-0.2)^2+0.2^2} \right \}$
Ya tenemos las 2 expresiones buscadas, con lo que podemos calcular la transformada $\mathbf{Z^{-1}}$de cada una de ellas:
$(42) \mathbf{Z^{-1}}\left \{\dfrac{z^2 -0.2z }{(z-0.2)^2+0.2^2} \right \}= (42)\sqrt{0.08}^k\; cos(bk)$
$(-42) \mathbf{Z^{-1}}\left \{\dfrac{0.2z }{(z-0.2)^2+0.2^2} \right \}= (-42)\sqrt{0.08}^k\; sen (bk)$
Con este paso ya hemos concluido y podemos poner la expresión definitiva de y(k):
$y(k) = 4.902 - 46.6667 (0.1)^k + 0.08^{k/2} 42 \left ( cos(bk)-sen(bk) \right )$, siendo $b = arccos(\sqrt{0.08})$.
Resolución del apartado b):
En primer lugar vamos a realizar la simulación creando la funcíón de transferencia mediante el comando de Matlab "tf".
El comando tf crea una función de transferencia con los exponentes positivos a partir de los coeficientes que acopañan a Z en el numerador y el denominador.
La función de transferencia ya la tenemos calculada anteriormente:
$ G(z) =\dfrac{z+2}{z^3-0.5z^2+0.12z-0.008}$
Por lo que los coeficientes del numerador y denominador quedarían así:
Numerador --> [1,2]
Denominador-->[1, -0.5,0.12, -0.008]
La función tf necesita un tercer parámetro que se corresponde con el periodo de muestreo. En nuestro caso no tendremos periodo de muestreo y lo indicaremos con un vector vacio [] como tercer parámetro.
La función quedaría de la siguiente forma:
G= tf([1,2], [1, -0.5,0.12, -0.008], []);
Para simular esta función con una entrada escalon usamos el comando de Matlab "step", al que pasamos la función G como parámetro.
[y1,k]= step(G);
y1 contendrá la salida del sistema tras aplicarle la función impulso como entrada.
k tiene un vector de coordenadas en el eje X con una serie de valores que da Matlab para ajustar la gráfica de una forma correcta.
A continuación realizaremos la misma simulación con el comando "filter"
El comando Filter de Matlab se utiliza para crear secuencias de ponderación. Sus tres parámetros son el vector A de constantes que acompañan a las Y(k), el vector B de constantes que acompañan a las U(k) y un tercer vector como entrada al sistema.
En nuestro caso el vector de entrada será una secuencia escalón. Para simularla crearemos un vector con todas las componentes a 1,simulando el comportamiento de la delta.
[1 1 1 1 .....]
Para ajustar el tamaño del vector en todas las representaciones utilizaremos el vector k obtenido con tf.
escalon=ones(size(k));
A continuación creamos los vectores con los coeficientes, tomándolos directamente de la ecuación en diferencias después de agrupar las Y(k) y U(k) a un lado y a otro de la igualdad:
$y(k)-0.5 y(k-1) +0.12 y(k-2)-0.008y(k-3) =u(k-2) + 2 u(k-3)$
B=[0,1,2];
A=[1,-0.5,0.12,-0.008]
Para simular capturamos en y2 los valores de la salida del sistema.
y2=filter(B,A,escalon);
La tercera simulación la realizamos con la ecuación obtenida en el apartado A de forma manual.
b=arcos(sqrt(0.08));
y3=4.902+42*(0.08).^(k/2).*cos(b*k)-42*(0.08).^(k/2).*1.03.*sin(b*k)-46.6667*0.1.^k;
Instrucciones en Matlab
clc,clear all,close all %%pagina CC-11 ejercicio b)
G=tf([1,2],[1,-0.5,0.12,-0.008],[]); %de la G(z) funcion de transferencia, ke es Y(Z)/U(Z)
k=0:20;
[y1,k]=step(G,k);%le damos la entrada.
entradaescalon=ones(size(k));
A=[1,-0.5,0.12,-0.008];%de la ecuacion de diferencias lo ke acompaña a la Y
B=[0,1,2];%lo que acompaña a la U
y2=filter(B,A,entradaescalon);
b=pi/4;%tenemos como raiz cuadrada de 0.08 de forma manual pero la ekivalencia es pi/4 y asi no perdemos tanta precision
y3=4.902+42*(0.08).^(k/2)*( cos(b*k)-sin(b*k) )-46.6667*0.1^k;
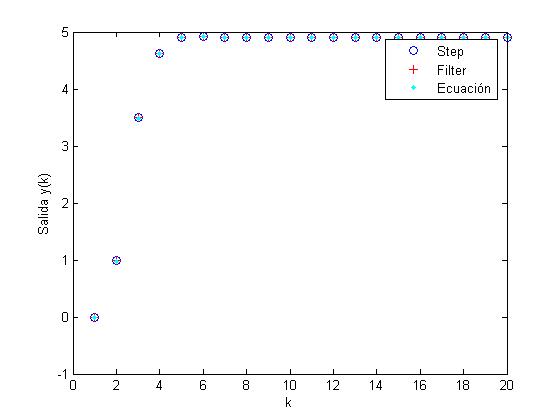
plot(k,y1,'bo',k,y2,'r+',k,y3,'.c')
xlabel('k'),ylabel('Salida y(k)')
legend('Step','Filter','Ecuación')
Grafica del ejercicio2:
Resolución del apartado c):
Haciendo el límite a y(k) obtenida en el apartado a) tenemos:
$\lim_ {k \rightarrow \infty}\, y(k) = \lim_ {k \rightarrow \infty} \, 4.902-46.6667*0.1^{k/2} \left ( -sen(bk)+cos(bk) \right ) = 4902.$
Es 4902 porque $0.1^k$ tiende a 0 al aumentar k, y la expresión formada por el seno y el coseno está acotada.
Aplicando el Teorema del Valor Final:
$y(\infty) = \lim_ {z \rightarrow 1} {\dfrac {(z-1)}{z}\, Y(z)} ={\dfrac{(z-1)}{z}.\dfrac{z}{z-1}.\dfrac{z+2}{z^3-0.5z^2+0.12z-0.008} \simeq 4.902}$
Ejercicios del Tema 2 Sistemas Muestreados :
Calcular la función de transferencia pulso de los siguientes sistemas en lazo cerrado...
- Primer sistema
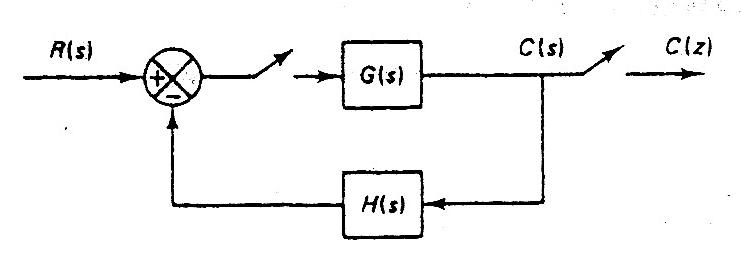
$ \begin{array}{l} Y(s) = E*(s) \cdot G(s) \to Y*(s) = E*(s) \cdot G*(s) \\ E(s) = R(s) - B(s) \to E*(s) = R*(s) - B*(s) \\ B(s) = Y(s) \cdot H(s) \to B*(s) = [Y(s) \cdot H(s)]* \\ ..... \\ E*(s) = R*(s) - B*(s) \\ E*(s) = R*(s) - [Y(s) \cdot H(s)]* \\ E*(s) = R*(s) - [E*(s) \cdot G(s) \cdot H(s)]* \\ E*(s) = R*(s) - E*(s) \cdot [G(s) \cdot H(s)]* \\ E*(s) = R*(s) - E*(s) \cdot GH*(s) \\ E*(s) + E*(s) \cdot GH*(s) = R*(s) \\ E*(s) \cdot [1 + GH*(s)] = R*(s) \\ E*(s) = \dfrac{{R*(s)}}{{1 + GH*(s)}} \\ ..... \\ Y*(s) = E*(s) \cdot G*(s) \\ Y*(s) = \dfrac{{R*(s)}}{{1 + GH*(s)}} \cdot G*(s) \\ Y(z) = \dfrac{{R(z)}}{{1 + GH(z)}} \cdot G(z) \\ \dfrac{{Y(z)}}{{R(z)}} = \dfrac{{G(z)}}{{1 + GH(z)}} \\ \end{array} $
- Segundo sistema

$ \begin{array}{l} E(s) = R(s) - B(s) \to E*(s) = R*(s) - B*(s) \\ Y(s) = E*(s) \cdot G(s) \to Y*(s) = E*(s) \cdot G*(s) \\ B(s) = Y*(s) \cdot H(s) \to B*(s) = Y*(s) \cdot H*(s) \\ ..... \\ E*(s) = R*(s) - B*(s) \\ E*(s) = R*(s) - Y*(s) \cdot H*(s) \\ E*(s) = R*(s) - E*(s) \cdot G*(s) \cdot H*(s) \\ E*(s) + E*(s) \cdot G*(s) \cdot H*(s) = R*(s) \\ E*(s) \cdot [1 + G*(s) \cdot H*(s)] = R*(s) \\ E*(s) = \dfrac{{R*(s)}}{{1 + G*(s) \cdot H*(s)}} \\ ..... \\ Y*(s) = E*(s) \cdot G*(s) \\ Y*(s) = \dfrac{{R*(s)}}{{1 + G*(s) \cdot H*(s)}} \cdot G*(s) \\ Y(z) = \dfrac{{R(z)}}{{1 + G(z) \cdot H(z)}} \cdot G(z) \\ \dfrac{{Y(z)}}{{R(z)}} = \dfrac{{G(z)}}{{1 + G(z) \cdot H(z)}} \\ \end{array} $
- Tercer sistema
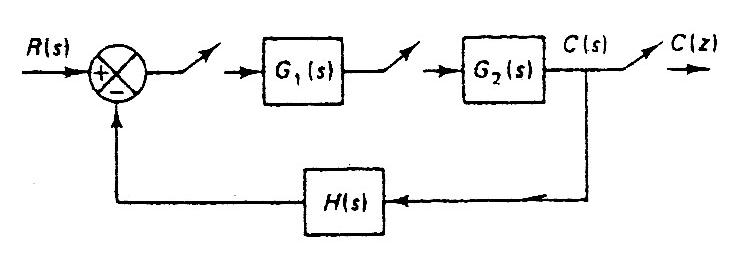
$\begin{array}{l} E(s) = R(s) - B(s) \to E*(s) = R*(s) - B*(s) \\ B(s) = Y(s) \cdot H(s) \to B*(s) = [Y(s) \cdot H(s)]* \\ Y(s) = U*(s) \cdot G_2 (s) \to Y*(s) = U*(s) \cdot G_2 *(s) \\ U(s) = E*(s) \cdot G_1 (s) \to U*(s) = E*(s) \cdot G_1 *(s) \\ \cdots \\ E*(s) = R*(s) - B*(s) \\ E*(s) = R*(s) - [Y(s) \cdot H(s)]*\\ E*(s) = R*(s) - [U*(s) \cdot G_2 (s) \cdot H(s)]* \\ E*(s) = R*(s) - U*(s) \cdot [G_2 (s) \cdot H(s)]* \\ E*(s) = R*(s) - U*(s) \cdot G_2 H*(s) \\ \cdots \\ U*(s) = E*(s) \cdot G_1 *(s) \\ U*(s) = [R*(s) - U*(s) \cdot G_2 H*(s)] \cdot G_1 *(s) \\ U*(s) = R*(s) \cdot G_1 *(s) - U*(s) \cdot G_2 H*(s) \cdot G_1 *(s) \\ U*(s) + U*(s) \cdot G_2 H*(s) \cdot G_1*(s) = R*(s) \cdot G_1 *(s) \\ U*(s) \cdot [1 + G_2 H*(s) \cdot G_1*(s)] = R*(s) \cdot G_1 *(s) \\ U*(s) = \dfrac{R*(s) \cdot G_1 *(s)}{1 +G_2 H*(s) \cdot G_1 *(s)} \\ \cdots \\ Y*(s) = U*(s) \cdot G_2 *(s) \\ \end{array}$
$\begin{array}{l}Y*(s) = \left[ \dfrac{R*(s) \cdot G_1 *(s)}{1 + G_2 H*(s) \cdot G_1 *(s)} \right] \cdot G_2 *(s) \\ Y*(s) = \dfrac{{R*(s) \cdot G_1 *(s) \cdot G_2 *(s)}}{{1 + G_2 H*(s) \cdot G_1 *(s)}} \\ Y(z) = \dfrac{{R(z) \cdot G_1 (z) \cdot G_2 (z)}}{{1 + G_2 H(z) \cdot G_1 (z)}} \\ \dfrac{{Y(z)}}{{R(z)}} = \dfrac{{G_1 (z) \cdot G_2 (z)}}{{1 + G_2 H(z) \cdot G_1 (z)}}\end{array}$
El esquema del problema es el siguiente:
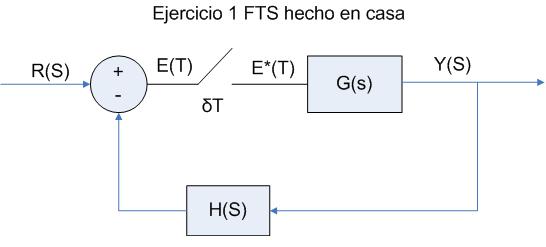
Como necesitamos la salida muestreada tenemos que colocar un muestreador imaginario al final del esquema, quedando de la siguiente forma:

Del cual sacamos las siguientes ecuaciones:
$1.$ $Y(s)=G(s)E^*(s)$
$2.$ $B(s)=H(s)Y(s)$
$3.$ $E(s)=R(s)-B(s)$
Y queremos obtener la funcion de transferencia pulso:
$\dfrac{Y(z)}{R(z)} \rightarrow \dfrac{Y^*(s)}{R^*(s)} $
Para ello resolvemos el sistema utilizando todas las ecuaciones:
1. $E(s)=R(s)-B(s)\rightarrow E^*(s)=[R(s)-B(s)]^*= R^*(s)-B^*(s)= R^*(s)-[Y(s)H(s)]^*=$
$R^*-[G(s)E^*(s)H(s)]^*=R^*-E(s)^*[G(s)H(s)]^* \rightarrow E^*(s)=\dfrac{R(s)}{1+GH^*(s)}$
Nótese que $GH^*(s)$ es $[G(s)H(s)]^*$.
2. $Y(s)=G(s)E^*(s) \rightarrow Y^*(s)=[G(s)E^*(s)]^*=E^*(s)G^*(s)$
Por lo tanto tenemos que nuestra funcion de transferencia pulso queda de la forma:
$Y^*(s)=\dfrac{R^*(s)}{1+GH^*(s)}G^*(s) \rightarrow \dfrac{Y^*(s)}{R^*(s)} = \dfrac{G^*(s)}{1+GH^*(s)}$
El esquema es el siguiente:
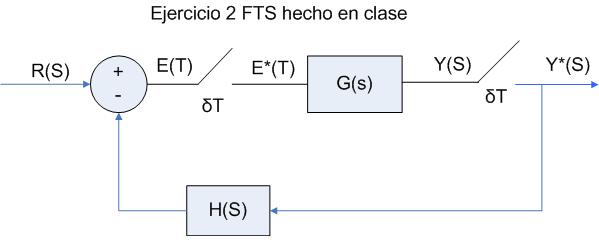
En este caso tenemos un muestreador con lo cual no nos hace falta porque obtenemos directamente Y*(s):
Las ecuaciones son las siguientes:
1. $E(s)=R(s)-B(s)$
2.$B(s)=H(s)Y^*(s)$ de estas dos primeras obtenemos $E(s)=R(s)-H(s)Y^*(s) \rightarrow E^*(s)=R^*(s)-H^*(s)Y^*(s)$
3.$Y(s)=G(s)E^*(s) \rightarrow Y^*(s)=E^*(s)G^*(s) \rightarrow Y^*(s)=R^*(s)G^*(s)-H^*(s)G^*(s)Y^*(s) $
$\rightarrow Y(s)^*[1+G^*(s)H^*(s)]=R^*(s)G^*(s)$
Finalmente, transformamos el sistema a dominio Z, sacamos factor comun Y^*(s):
$\dfrac{Y(z)}{R(z)}=\dfrac{G(z)}{1+G(z)H(z)}$
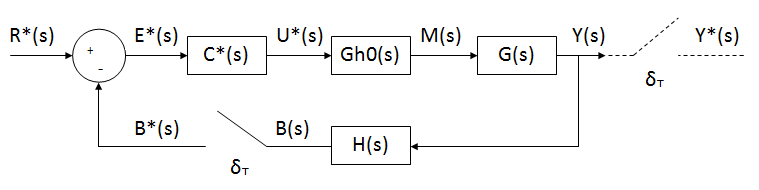
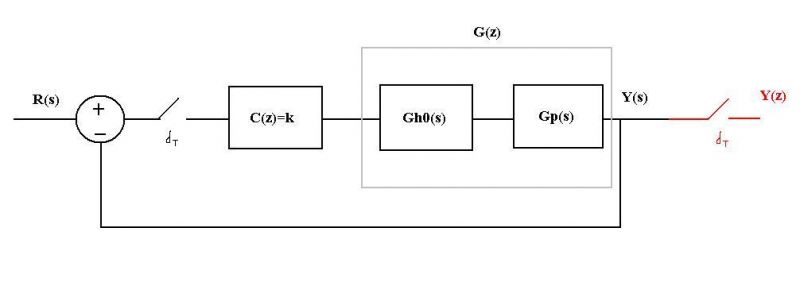
Ecuaciones del sistema:
$1. $ $E^*(s)=R^*(s)-B^*(s)$
$2.$ $U^*(s)=E^*(s)C^*(s)$
$3.$ $M(s)=Gh0(s)U^*(s)$
$4.$ $Y(s)=M(s)G(s)$
$5.$ $B(s)=Y(s)H(s)$
Vamos a obtener $E^*(s)$:
$E^*(s)=R^*(s)-B^*(s)=R^*(s)-[Y(s)H(s)]^*=R^*(s)-[M(s)G(s)H(s)]^*=R^*(s)-[Gh0(s)U^*(s)G(s)H(s)]^*$
$E^*(s)=R*(s)-U^*(s)*[Gh0(s)G(s)H(s)]^*=R^*(s)-E^*(s)C^*(s)[Gh0(s)G(s)H(s)]^*$
$E^*(s)=\dfrac{R^*(s)}{1+C^*(s)*[Gh0(s)G(s)H(s)]^*}$
Desarrollamos $Y(s)$ hasta llegar a una expresión que contenga $E^*(s)$:
$Y(s)=M(s)G(s)=Gh0(s)U^*(s)G(s)=E^*(s)C^*(s)Gh0(s)G(s)$
$Y(s)=\dfrac{C^*(s)Gh0(s)G(s)R^*(s)}{1+C^*(s)*[Gh0(s)G(s)H(s)]^*}$
$Y^*(s)=\dfrac{C^*(s)R^*(s)*[Gh0(s)G(s)]^*}{1+C^*(s)*[Gh0(s)G(s)H(s)]^*}$
$\dfrac{Y^*(s)}{R^*(s)}=\dfrac{C^*(s)*[Gh0(s)G(s)]^*}{1+C^*(s)*[Gh0(s)G(s)H(s)]^*}$
Realizamos el cambio $Gh0(s)=\dfrac{1-e^{-Ts}}{s}$
$\dfrac{Y^*(s)}{R^*(s)}=\dfrac{C^*(s)*[\dfrac{1-e^{-Ts}}{s}G(s)]^*}{1+C^*(s)*[\dfrac{1-e^{-Ts}}{s}G(s)H(s)]^*}$
$1-e^{-Ts}$ está muestrado y se representa como $F^*(s)$
$\dfrac{Y^*(s)}{R^*(s)}=\dfrac{C^*(s)F^*(s)*[\dfrac{G(s)}{s}]^*}{1+C^*(s)F^*(s)*[\dfrac{G(s)H(s)}{s}]^*}$
Aplicamos transformada Z, teniendo en cuenta:
$F^*(s)=1-e^{-Ts}$ y $z=e^{Ts}$
$\dfrac{Y(z)}{R(z)}=\dfrac{C(z)F(z)*Z\lbrace\dfrac{G(s)}{s}\rbrace}{1+C(z)F(z)*Z\lbrace\dfrac{G(s)H(s)}{s}\rbrace}=\dfrac{C(z)(1-z^{-1})*G_1(z)}{1+C(z)(1-z^{-1})*G_1H(z)}$, siendo $G_1(s) = \dfrac{G(s)}{s}$.
A continuación se listan ejercicios de exámenes o trabajos de diseño, resueltos o no, de la asignatura Control por Computador.
Tenga en cuenta que estos ejercicios han podido ser enviados por cualquier usuario de la web, por lo que no sea crítico con los resultados (pueden contener errores). Edite el contenido si observa algún error.
Por favor, si resuelve algún ejercicio cámbiele el título, de forma que refleje que está resuelto (poner "Resuelto" al principio del título).
Si desea imprimirse todos los ejercicios de una sola vez, pulse en esta página "Versión para imprimir". Lo mismo puede hacer sobre la página anterior para obtener todos los apuntes de Control por Computador.
Para añadir nuevos ejercicios dele a "Añadir página hija".
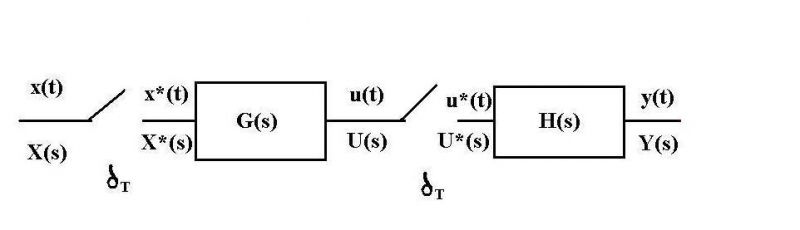
Para hallar la función de transferencia pulso de este sistema tenemos que calcular
$\dfrac{Y(z)}{X(z)}$
Necesitamos conocer la salida en los instantes de muestreo por lo que colocaremos un muestreador imaginario ideal en la salida del sistema y supondremos que los periodos de muestreo de todos los muestreadores son el mismo.

De esta forma podemos calcular Y*(s) para a partir de ella calcular Y(z).
Ahora vamos a calcular Y*(s):
Tenemos que $Y(s)=U*(s)H(s)$
Para obtener Y*(s) tenemos que muestrear Y(s), por lo tanto tenemos que:
$Y(s)=[U*(s)H(s)]*$
A su vez, U*(s) lo calculamos a partir de un muestreo sobre U(s), que lo calcularemos a partir de G(s) y X*(s)
$U*(s)=[U(s)]*=[X*(s)G(s)]*$
Como el muestreo de una señal muestreada con el mismo periodo nos da la misma señal, podemos sacarla del muestreo.
$U*(s)=X*(s)[G(s)]*$
Sustituyendo en Y*(s) tenemos:
$Y*(s)=X*(s)[G(s)]*[H(s)]*$
Haciendo el cambio z=e^{aT} tenemos
$Y(z)=X(z)Z\{G(s)\}Z\{H(s)\}$
Ahora calcularemos G(z) y H(z)
$G(z)=\mathbf{Z}\{G(s)\}=Z\lbrace\dfrac{1}{s+a}\rbrace=\dfrac{z}{z-e^{-aT}}$
$H(z)=\mathbf{Z}\{H(s)\}=Z\{\dfrac{1}{s+b}\}=\dfrac{z}{z-e^{-bT}}$
Ahora podemos calcular la función transferencia pulso.
$\dfrac{Y(z)}{X(z)}=G(z)H(z)$
$\dfrac{Y(z)}{X(z)}=\dfrac{z}{z-e^{-aT}}\dfrac{z}{z-e^{-bT}}=\dfrac{z^2}{(z-e^{-aT})(z-e^{-bT})}$
Vamos a estudiar la estabilidad del siguiente sistema teniendo en cuenta que la función de transferencia de G(z) es
$G(z)=\dfrac{0.3679z+0.2642}{(z-0.3679) (z-1)}$
Vamos a obtener la función de transferencia del sistema en lazo cerrado.
$\dfrac{Y(z)}{R(z)}$
$E(s)=R(s)-Y(s)$ que de forma discreta es $E(z)=R(z)-Y(z)$
$U(z)=K E(z)$
$Y(z)=U(z)G(z)$
De las dos primeras ecuaciones obtenemos
$U(z)=K(R(z)-Y(z))=KR(z)-KY(z)$
Utilizando U(z) en la ecuación de Y(z) obtenemos
$Y(z)=U(z)G(z)=KR(z)G(z)-KY(z)G(z)$
$Y(z)(1+KG(z))=KR(z)G(z)$
Teniendo finalmente la función de transferencia pulso del sistema
$\dfrac{Y(z)}{R(z)}=\dfrac{KG(z)}{1+KG(z)}=$
La ecuación característica de un sistema es el denominador de la función de transferencia en lazo cerrado. Por lo tanto en nuestro ejemplo la ecuación característica es:
$E.C. \equiv 1+KG(z)=0$
Sustituyendo G(z) por el valor que nos indica el problema tenemos que:
$E.C.\equiv(1+K)\dfrac{0.3679z+0.2642}{(z-0.3679) (z-1)}=0$
Para aplicar el test de Jury tenemos que tener la ecuación característica en forma de polinomio, por lo que vamos a quitar el denominador de la fracción.
$(z-0.3679) (z-1)+K(0.3679z+0.2642)=0$
$z^2-1.3679z+0.3679+0.3679Kz+0.2642K=0$
$z^2+z(0.3679K-1.3679)+0.2642K+0.3679=0$
Una vez colocada en forma de polinomio vamos a aplicar el test de Jury. La matriz del test tendrá un número de filas 2n-3, siendo n el grado de la ecuación característica. En este caso 2n-3=2*2-3=1.

Condiciones del test de Jury
Ahora vamos a comprobar las condiciones del test para comprobar la estabilidad según los valores de K y de la E.C.
1) D(1)>0 Tenemos que comprobar que el valor de la E.C. evaluado en z=1 es mayor que 0.
$1+1(0.3679K-1.3679)+0.2642K+0.3679>0$
$(0.3679+0.2642)K>0$
Para que se cumpla esta inecuación, forzosamente K tiene que ser mayor que 0
2) $(-1)^n D(-1) >0$ Tenemos que comprobar que -1 elevado al grado de la ecuación multiplicado por la ecuación evaluada en z=-1 es mayor que 0. Como n=2, -1 elevado a 2 es 1, por lo que solo vamos a evaluar E.C. en z=-1.
$-1+(-1)(0.3679K-1.3679)+0.2642K+0.3679>0$
$1-0.3679K+1.3679+0.2642K+0.3679>0$
$2.7358-0.1037K>0$
$-K>\dfrac{-2.7358}{0.1037};K<26.382$
3) | a0 | < an Esta condición la comprobamos utilizando la tabla del test de Jury. Como solo esta formada por una fila, tenemos que evaluar únicamente una condición.
$0.2642K+0.3679<1$
$K<\dfrac{1-0.2642}{0.3679};K<2.3925$
Finalmente acotamos el valor de K para que cumpla las 3 inecuaciones obtenidas.
$1) K>0$
$2) K<26.382$
$3) K<2.3925$
Las que nos van a condicionar el valor de K son las inecuaciones 1 y 3, que nos van a limitar el valor de K para que sea estable. Por lo tanto K queda acotada de la siguiente forma:
$0< K<2.39$
nota: redondeamos en este caso a la baja para asegurarnos un margen a la hora de asignar un valor concreto a K.
De esta forma el sistema obtenido será estable.
Se desea controlar la posición angular de un motor de corriente continua que servirá como articulación para un brazo robot. Para ello se ha estudiado la dinámica de dicho motor junto con su etapa de potencia, la reductora empleada para mover el brazo y el potenciómetro que se empleará como sensor de la posición angular del mismo. El modelo obtenido es:
$$Gp(s) = \dfrac{{V_{pot} (s)}}{{U(s)}} = \dfrac{{10}}{{s(s + 1)}},$$
siendo $V_{pot} (s)$ la tensión del potenciómetro de salida (función directa del ángulo en el que está situado el motor), y U(s) la tensión de entrada a la etapa de potencia del motor. El esquema de control empleado es el mostrado en la siguiente figura:
siendo $V_{in} (s)$ la entrada de referencia (tensión) del sistema, $C(z)$ el controlador digital y$G_p (s)$ la función de transferencia de la planta a controlar. El conversor analógico-digital se considerará como un muestreador impulsivo, y el digital analógico como un retenedor de orden 0.
Procedimiento de diseño:
1) Obtener la función de transferencia pulso del sistema en lazo cerrado
Para poder trabajar con la transformada Z, colocamos un muestreador virtual a la salida del sistema, quedando de la siguiente manera:
El conversor analógico-digital es un muestreador impulsivo y el conversor digital-analógico es un retenedor de orden cero con la siguiente función de transferencia:
$G_{h0} (s) = \dfrac{1 - e^{Ts}}{s}$
Para el cálculo de la función de transferencia del sistema, agrupamos en un solo bloque el retenedor de orden cero y la planta, quedando el diagrama de la siguiente manera:
Realizamos los cálculos para despejar la función de transferencia:
$\begin{array}{l} V_{pot} (s) = G_1 (s)U^* (s) \\
U^* (s) = C(z)E^* (s) \\
E^* (s) = \left[ {V_{in} (s) - V_{pot} (s)} \right]^* \\
\end{array}$
Despejamos:
$\begin{array}{l} E^* (s) = \left[ {V_{in} (s) - V_{pot} (s)} \right]^* = V_{in} ^* (s) - V_{pot} ^* (s) \\
V_{pot} ^* (s) = \left[ {G_1 (s)U^* (s)} \right]^* = G_1 ^* (s)U^* (s) = G_1 ^* (s)C(z)E^* (s) = \\
= G_1 ^* (s)C(z)\left[ {V_{in} ^* (s) - V_{pot} ^* (s)} \right] \\
\end{array}$
Finalmente, la última expresión queda de la siguiente manera:
$\begin{array}{l}
V_{pot} ^* (s)\left[ {1 + G_1 ^* (s)C(z)} \right] = G_1 ^* (s)C(z)V_{in} ^* (s) \\
\dfrac{{V_{pot} ^* (s)}}{{V_{in} ^* (s)}} = \dfrac{{G_1 ^* (s)C(z)}}{{1 + G_1 ^* (s)C(z)}} \\
\end{array}$
Expresando todo en Z, la función de transferencia queda:
$G_{LC} (z) = \dfrac{{V_{pot} (z)}}{{V_{in} (z)}} = \dfrac{{G_1 (z)C(z)}}{{1 + G_1 (z)C(z)}}$
2) Simular el comportamiento del sistema con $C(z) = 1$, para una entrada de tipo escalón y para una entrada de tipo rampa. Comente los resultados de la simulación teniendo en cuenta el significado de las señales que se representan.
Como el controlador no tiene ningún efecto, omitimos los conversores A/D.
Simulamos la entrada escalón: (Cuidado, esta simulación puede no ser correcta)
H = tf(10,[1 1 10]);
T = 0:0.1:15;
Y = step(H,T);
X = ones(1,length(T));
hold on;
plot(T,Y,'b');
plot(T,X,'r');
Se observa que el sistema es subamortiguado, y que tarda en estabilizarse aproximadamente unos 7,5s. El sobreimpulso es excesivo, ya que es aproximadamente del 60%. También se observa que el error de estado estacionario de posición es nulo, puesto que es sistema es de tipo 1.
Simulamos la entrada rampa de pendiente 1: (Cuidado, esta simulación puede no ser correcta)
H = tf(10,[1 1 10]);
T = 0:0.1:10;
Y = lsim(H,T,T);
hold on;
plot(T,Y,'b');
plot(T,T,'r');
Es esta respuesta se obsera obviamente la misma dinámica que en la respuesta anterior, es decir, la de un sistema subamortiguado con un gran sobreimpulso. Sin embargo, el error de velocidad no es nulo como lo era el de posición, ya que es aproximadamente del 10%.
Para medir el error mediante MATLAB, puede teclearse:
error_velocidad=Y(end)-T(end)
3) Diseñar el controlador $C(z)$ mediante el Lugar Geométrico de las Raíces, para que el tiempo de asentamiento sea, según el criterio del 2%, inferior a 2s, y el sobreimpulso máximo no supere el 5%. Para ello obtenga en primer lugar los polos que debería tener un sistema en tiempo continuo para cumplir las especificaciones, y calcule a partir de éstos los de un sistema discreto. En último lugar, utilice el L.G.R. para situar los polos de lazo cerrado del sistema aprocimadamente en el punto calculado.
Calculamos los polos teóricos de tiempo continuo que cumplan las especificaciones:
$\delta = \sqrt {\dfrac{{\ln ^2 (M_p )}}{{\ln ^2 (M_p ) + \pi }}}$
$\omega _n = \dfrac{4}{{\delta T_s }}$
$p_{1,2} (s) = - \delta \omega _n \pm j\omega _n \sqrt {1 - \delta ^2 }$
Resolviendo, para T=0.1:
delta = sqrt((log(Mp)^2) / (pi^2 + log(Mp)^2))
wn = 4 / (delta * ts)
p1 = -delta * wn + j * wn * sqrt(1 - delta^2)
p2 = -delta * wn - j * wn * sqrt(1 - delta^2)
Obtenemos los polos en tiempo continuo que cumplen las especificaciones:
p1 = -2.0000 + 2.0974i
p2 = -2.0000 - 2.0974i
Para obtener los valores en tiempo discreto solo tenemos que realizar:
p1z = exp(T * p1)
p2z = exp(T * p2)
Obtenemos los polos en tiempo discreto:
p1 = 0.8008 + 0.1705i
p2 = 0.8008 - 0.1705i
Observando en la herramienta sisotool la estabilidad del sistema nos damos cuenta que a partir de K=0.16 el sistema se vuelve inestable:
Obtenemos el siguiente controlador:
$C(z) = 0.16 \cdot \dfrac{1}{{1 + 0.58z^{ - 1} + (0.38z^{ - 1} )^2 }}$
4) Simular el comportamiento del sistema con el controlador diseñado para una entrada de tipo escalón y para una entrada de tipo rampa. Comente los resultados de la simulación.
Simulamos la entrada escalón:
clear all, close all, clc;
T = 0.1;
% Constantes
G = tf(10, [1 1 0]);
C = tf([0.16 0 0], [1 0.58 0.1444],T);
Gz = c2d(G,T);
GC = Gz*C;
T = 0:0.1:15;
GLC1 = GC/(1+GC);
Y = step(GLC1,T);
X = ones(1,length(T));
hold on;
plot(T,Y,'b');
plot(T,X,'r');
Vemos que el sistema se va estabilizando en torno al valor 1, con alguna pequeña oscilación, pero respetando los valores indicados.
Para una entrada tipo rampa de pendiente 1:
clear all, close all, clc;
T = 0.1;
% Constantes
G = tf(10, [1 1 0]);
C = tf([0.16 0 0], [1 0.58 0.1444],T);
Gz = c2d(G,T);
GC = Gz*C;
T = 0:0.1:10;
GLC1 = GC/(1+GC);
Y = lsim(GLC1,T,T);
hold on;
plot(T,Y,'b');
plot(T,T,'r');
Se observa un error de estado estacionario de aproximadamente valor 1. Este error es debido a que el sistema con el controlador es de tipo 1.
5) Obtenga el algoritmo de control mediante el método directo para el controlador diseñado y programe mediante pseudo-código dicho algoritmo.
$C(z) = \dfrac{{Y(z)}}{{X(z)}} = \dfrac{1}{{1 + 0.58z^{ - 1} + 0.1444z^{ - 2} }}$
$Y(z) \cdot (1 + 0.58z^{ - 1} + 0.1444z^{ - 2} ) = X(z)$
$Y(z) + 0.58z^{ - 1} Y(z) + 0.1444z^{ - 2} Y(z) = X(z)$
Pasamos a ecuaciones diferenciales:
$Y[n] + 0.58 \cdot Y[n - 1] + 0.1444 \cdot Y[n - 2] = X[n]$
$Y[n] = X[n] - 0.58 \cdot Y[n - 1] - 0.1444 \cdot Y[n - 2]$
Este pseudo-código está mal, hay que programar el algoritmo de control, es decir C(z):
pseudo-código:
Funcion Y=Y(n)
Si n=0 entonces retorna Y=0.144
Si n=1 entonces retorna Y=0.58
Si n>1 entonces retorna Y=X(n)-0.58*Y(n-1)-0.144*Y(n-2)
Enlaces:
[1] http://es.wikipedia.org/wiki/Delta_de_Kronecker