2010, septiembre. Ejercicio 2 (5 puntos)

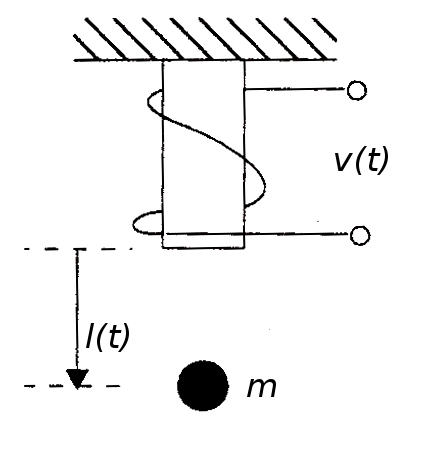
En la figura se puede observar el esquema simplificado de un sistema de levitación magnética similar al utilizado por los trenes de última tecnología. El campo magnético generado en la bobina a partir de la tensión de entrada $v(t)$, provoca la elevación de la bola de metal de masa m, de forma que controlando adecuadamente la tensión de entrada puede mantenerse suspendida la masa a una distancia $l(t)$ determinada. Dado el conjunto de ecuaciones que gobierna la dinámica del sistema, se desea estudiar el comportamiento del mismo, para lo cual se solicita:

$m \dfrac{\text{d}^2 l(t)}{\text{d} t^2} = m g - \dfrac{i(t)^2}{l(t)}$ $v(t) = R i(t) + L \dfrac{\text{d}i(t)}{\text{d}t}$ Masa → $m = 0.01 kg$ Inductancia del bobinado → $L = 0.1 H$ Resistencia del bobinado → $R = 10 \Omega$ Aceleración de la gravedad → $g = 9.8 m/s ^2$ Distancia de la masa al electroimán → $l(t) > 0$  (en mm)

1. Utilice las ecuaciones anteriores para obtener un modelo de estado del sistema.
2. Determine el estado de equilibrio del sistema para $v(t) = v_{eq} =10 V$.
3. Linealice el sistema en el estado de equilibrio obtenido. ¿Es este estado de equilibrio estable? Argumente su respuesta. Recuerde que:$$\dot{\mathbf{x}} \simeq \mathbf{A} (\mathbf{x} - \mathbf{x}_{eq}) + \mathbf{B} (\mathbf{u} - \mathbf{u}_{eq})$$

   $${\small \mathbf{A} = \left.\left(\begin{array}{cccc} \dfrac{\partial f_1}{\partial x_1} & \dfrac{\partial f_1}{\partial x_2} & \cdots & \dfrac{\partial f_1}{\partial x_n}\\ \dfrac{\partial f_2}{\partial x_1} & \dfrac{\partial f_2}{\partial x_2} & \cdots & \dfrac{\partial f_2}{\partial x_n}\\ \cdots & \cdots & \ddots & \cdots\\ \dfrac{\partial f_n}{\partial x_1} & \dfrac{\partial f_n}{\partial x_2} & \cdots & \dfrac{\partial f_n}{\partial x_n}\\ \end{array}\right)\right|_{ \begin{array}{l} \mathbf{x}=\mathbf{x}_{eq}\\ \mathbf{u}=\mathbf{u}_{eq} \end{array} } }$$

   $${\small \mathbf{B} = \left.\left(\begin{array}{cccc} \dfrac{\partial f_1}{\partial u_1} & \dfrac{\partial f_1}{\partial u_2} & \cdots & \dfrac{\partial f_1}{\partial u_m}\\ \dfrac{\partial f_2}{\partial u_1} & \dfrac{\partial f_2}{\partial u_2} & \cdots & \dfrac{\partial f_2}{\partial u_m}\\ \cdots & \cdots & \ddots & \cdots\\ \dfrac{\partial f_n}{\partial u_1} & \dfrac{\partial f_n}{\partial u_2} & \cdots & \dfrac{\partial f_n}{\partial u_m}\\ \end{array}\right)\right|_{ \begin{array}{l} \mathbf{x}=\mathbf{x}_{eq}\\ \mathbf{u}=\mathbf{u}_{eq} \end{array} } }$$

4. Simule el comportamiento del sistema linealizado durante 2 segundos partiendo de un punto cercano al estado de equilibrio. Represente cada variable de estado en una gráfica. Comente e interprete los resultados obtenidos en la simulación.
5. Simule el comportamiento del sistema no lineal durante 2 segundos partiendo del mimo punto anterior. Represente cada variable de estado en una gráfica. Comente e interprete los resultados de la simulación.