CAPÍTULO 3

Análisis del comportamiento dinámico de los sistemas

Este capítulo generaliza el concepto de modelo de estado, tanto desde el punto de vista continuo como discreto. Así se verá como recorrer el amplio espectro existente entre el caso más general, léase sistema no lineal variante con el tiempo, al más particular, sistema lineal e invariante con el tiempo. Esto es muy importante porque el lector debe tener siempre claro el rango de validez del modelo que está utilizando, de modo que debe evitar tanto cometer errores de modelado inasumibles, como sobreesfuerzos inútiles; ya que la mayoría de las veces los modelos admiten simplificaciones dentro de un rango de funcionamiento. A partir del modelo de estado de un sistema se pueden extraer múltiples enseñanzas de su comportamiento dinámico. Quizás la primera sea conocer la naturaleza de sus estados de equilibrio (o puntos singulares de su espacio de estado). Cuando el sistema es lineal, sólo puede tener un estado de equilibrio o un conjunto continuo de ellos (si la ecuación diferencial que lo modela no tiene término independiente); sin embargo, los sistemas no lineales pueden tener más de un estado de equilibrio. El análisis de los sistemas en su plano de fase (espacio de estado para sistemas de orden 2) caracteriza de forma cualitativa su comportamiento dinámico. Para los sistemas lineales éste depende sólo del carácter del estado de equilibrio, el cual queda definido por los autovalores de la matriz de estado; sin embargo, cuando los sistemas son no lineales, el carácter de los estados de equilibrio no es suficiente para entender su comportamiento global. Tanto es así que la riqueza dinámica de los mismos lleva a comportamientos sorprendentes, como los ciclos límite en los sistemas de orden 2 o incluso el caos en los de orden 3. Por último, si bien el conocimiento del comportamiento global de las trayectorias de un sistema no lineal puede ser una tarea muy compleja, el conocimiento local en torno a sus estados de equilibrio requiere menos esfuerzo, la mayoría de las veces basta con linealizar el sistema en torno a dichos estados. A partir de ahí, el estudio de los autovalores de la matriz de estado resultante (la matriz Jacobiana en este caso) permite realizar interpretaciones locales similares a las realizadas a nivel global para los sistemas lineales.

3.1 Modelo de estado de un sistema general. Casos especiales

Si bien en el capítulo anterior nuestro estudio se ha centrado en los sistemas lineales, bien porque puedan ser considerados como tales o porque puedan ser linealizados en una zona concreta de funcionamiento, el mundo que nos rodea es esencialmente no lineal. En consecuencia, se ha de tener siempre muy presente esta circunstancia, de modo que el deseo lógico de simplificar los problemas (hacerlos lineales) no lleve a cometer errores inasumibles.
En base a la visión adquirida en el capítulo anterior, en esta sección se va a generalizar el con-cepto de modelo de estado. Así, un sistema completamente general (se entiende que puede ser no lineal y variante con el tiempo) puede ser representado por un modelo de estado consistente en un número finito de ecuaciones diferenciales de primer orden:

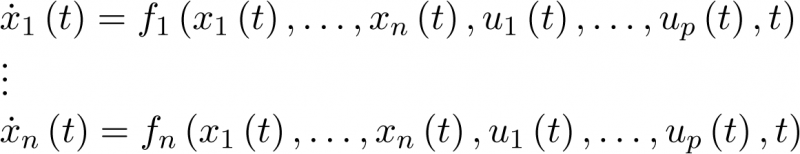(3.1)

Definiendo los vectores

${\bf{\dot x}}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ \vdots \\ {{{\dot x}_n}\left( t \right)} \\ \end{array}} \right);\,\,\,\,{\bf{u}}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{u_1}\left( t \right)} \\ \vdots \\ {{u_p}\left( t \right)} \\ \end{array}} \right);\,$ $\,{\bf{f}}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right),t} \right) = \left( {\begin{array}{*{20}{c}} {{f_1}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right),t} \right)} \\ \vdots \\ {{f_n}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right),t} \right)} \\ \end{array}} \right)$

(3.2)

La ecuación (3.1) puede ser escrita de la forma compacta

$\,{\bf{\dot x}}\left( t \right) = \,{\bf{f}}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right),t} \right)$

(3.3)

Del mismo modo, la ecuación de salida del sistema se escribirá como

$\,{\bf{y}}\left( t \right) = \,{\bf{h}}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right),t} \right)$

(3.4)

Las ecuaciones (3.3) y (3.4) representan el modelo de estado en tiempo continuo de un sistema completamente general.
Si las ecuaciones de estado y salida anteriores son lineales en el estado x y en la entrada u, el modelo puede ser representado como

$\begin{array}{*{20}{c}} {{\bf{\dot x}}\left( t \right) = \,{\bf{A}}\left( t \right){\bf{x}}\left( t \right) + {\bf{B}}\left( t \right){\bf{u}}\left( t \right)} \\ {{\bf{y}}\left( t \right) = \,{\bf{C}}\left( t \right){\bf{x}}\left( t \right) + {\bf{D}}\left( t \right){\bf{u}}\left( t \right)} \\ \end{array},$

(3.5)
(3.6)

Donde las dimensiones de los vectores y las matrices ya fueron definidas en el capítulo anterior. Si el sistema además de lineal es invariante (LTI), las matrices tienen sus elementos constantes, con lo cual el modelo se escribirá en la forma ya conocida siguiente:

$\,\begin{array}{*{20}{c}} {{\bf{\dot x}}\left( t \right) = \,{\bf{Ax}}\left( t \right) + {\bf{Bu}}\left( t \right)} \\ {\,{\bf{y}}\left( t \right) = \,{\bf{Cx}}\left( t \right) + {\bf{Du}}\left( t \right)} \\ \end{array}.$

(3.7)
(3.8)

El modelo de estado general (3.3) – (3.4) se escribirá para tiempo discreto en la forma

$\begin{array}{*{20}{c}} {{\bf{x}}\left( {k + 1} \right) = \,{{\bf{f}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right),{\bf{u}}\left( k \right),k} \right)} \\ {{\bf{y}}\left( k \right) = \,{{\bf{h}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right),{\bf{u}}\left( k \right),k} \right)} \\ \end{array}.$

(3.9)
(3.10)

Del mismo modo que en el caso continuo, si las ecuaciones anteriores son lineales en el estado y en la entrada, el modelo puede ser representado como

$\,\begin{array}{*{20}{c}} {{\bf{x}}\left( {k + 1} \right) = \,{{\bf{A}}_{\bf{k}}}\left( k \right){\bf{x}}\left( k \right) + {{\bf{B}}_{\bf{k}}}\left( k \right){\bf{u}}\left( k \right)} \\ {\,{\bf{y}}\left( k \right) = \,{{\bf{C}}_{\bf{k}}}\left( k \right){\bf{x}}\left( k \right) + {{\bf{D}}_{\bf{k}}}\left( k \right){\bf{u}}\left( k \right)} \\ \end{array}$

(3.11)

Por último, para el caso LTI,

$\,\begin{array}{*{20}{c}} {{\bf{x}}\left( {k + 1} \right) = \,{{\bf{A}}_{\bf{k}}}{\bf{x}}\left( k \right) + {{\bf{B}}_{\bf{k}}}{\bf{u}}\left( k \right)} \\ {\,{\bf{y}}\left( k \right) = \,{{\bf{C}}_{\bf{k}}}{\bf{x}}\left( k \right) + {{\bf{D}}_{\bf{k}}}{\bf{u}}\left( k \right)} \\ \end{array}$

(3.12)

Casos especiales

Ecuación de estado no forzada. Se da cuando la entrada externa al sistema es idénticamente cero, en cuyo caso la ecuación de estado (3.3) se escribe como

$\,{\bf{\dot x}}\left( t \right) = \,{\bf{f}}\left( {{\bf{x}}\left( t \right),t} \right)$

(3.13)

Nótese que la ecuación no forzada (3.13) tendrá esa misma expresión tanto si 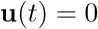${\bf{u}}\left( t \right) = 0$ como si u(t) se obtiene a partir del vector de estado, 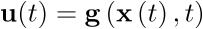${\bf{u}}\left( t \right) = {\bf{g}}\left( {{\bf{x}}\left( t \right),t} \right)$ ; ya que sustituyendo 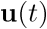${\bf{u}}\left( t \right)$ en (3.3), éste se elimina y vuelve a quedar la ecuación no forzada (3.13).

Sistema autónomo. Se da cuando el argumento de la función dada en (3.13) no depende del tiempo, en cuyo caso la ecuación de estado del sistema se escribe en la forma siguiente:

$\,{\bf{\dot x}}\left( t \right) = \,{\bf{f}}\left( {{\bf{x}}\left( t \right)} \right)$

(3.14)

Los sistemas autónomos son de importancia especial en automática y cumplen, entre otras propiedades, la de ser invariantes a cambios en el origen del tiempo. Esto quiere decir que si la variable t es cambiada por 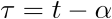$\tau = t - \alpha$ , la ecuación de estado permanece invariante.
Los casos especiales (3.13) y (3.14) siguen siendo igualmente válidos para tiempo discreto, sin más que cambiar t por k, FALTAAAAAAAAAA(${\bf{\dot x}}\left( t \right)$) por 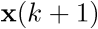${\bf{x}}\left( {k + 1} \right)$ y f por f_k.

Ejemplo 3.1. Sistema mecánico no lineal. En el ejemplo 2.1 se resolvió el sistema muelle – masa – resorte para el caso en que todos sus elementos eran lineales. Supóngase ahora que el com-portamiento del muelle no es lineal, de modo que la fuerza necesaria para estirarlo aumenta con el desplazamiento del modo siguiente:

$\,{f_k}\left( t \right) = \,ky\left( t \right)\left( {1 + \alpha {y^2}\left( t \right)} \right)$

(3.15)

Donde 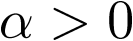$\alpha > 0$ es una constante. Ahora, la ecuación diferencial (2.2) se escribirá como

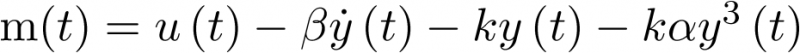$m\ddot y\left( t \right) = u\left( t \right) - \beta \dot y\left( t \right) - ky\left( t \right) - k\alpha {y^3}\left( t \right)$

(3.16)

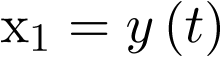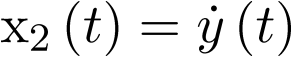Designando las variables de estado como ${x_1} = y\left( t \right)$ y ${x_2}\left( t \right) = \dot y\left( t \right)$ , se tiene en la ecuación anterior que

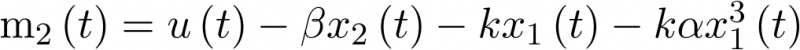$m{\dot x_2}\left( t \right) = u\left( t \right) - \beta {x_2}\left( t \right) - k{x_1}\left( t \right) - k\alpha x_1^3\left( t \right)$

(3.17)

A partir de aquí la ecuación vectorial de estado se obtiene de forma inmediata:

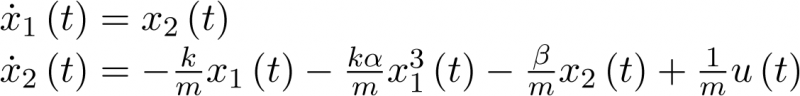$\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right) = {x_2}\left( t \right)} \hfill \\ {{{\dot x}_2}\left( t \right) = - \frac{k}{m}{x_1}\left( t \right) - \frac{{k\alpha }}{m}x_1^3\left( t \right) - \frac{\beta }{m}{x_2}\left( t \right) + \frac{1}{m}u\left( t \right)} \hfill \\ \end{array}$

(3.18)

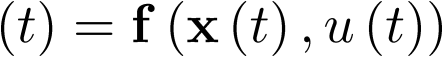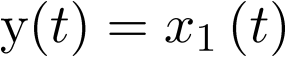Nótese que la ecuación anterior es de la forma ${\bf{\dot x}}\left( t \right) = {\bf{f}}\left( {{\bf{x}}\left( t \right),u\left( t \right)} \right)$ , donde f es una función no lineal en el estado ${\bf{x}}\left( t \right)$ ; sin embargo, en este caso concreto, la ecuación de salida de este sistema, $y\left( t \right) = {x_1}\left( t \right)$ , es lineal.
En particular, si 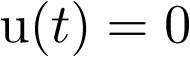$u\left( t \right) = 0$ , la ecuación (3.18) se transforma en el sistema autónomo no lineal 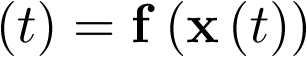${\bf{\dot x}}\left( t \right) = {\bf{f}}\left( {{\bf{x}}\left( t \right)} \right)$ siguiente:

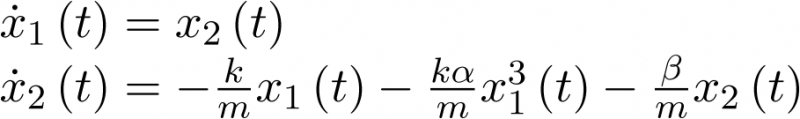(3.19)

Por supuesto, la no consideración¹ [1] del término no lineal $x_1^3\left( t \right)$ en (3.18) conduce al sistema lineal ya visto en (2.2):

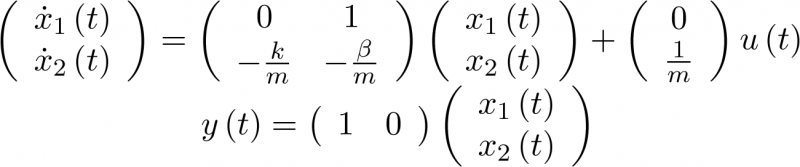$\begin{array}{c} \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 & 1 \\ { - \frac{k}{m}} & { - \frac{\beta }{m}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ {\frac{1}{m}} \\ \end{array}} \right)u\left( t \right) \\ y\left( t \right) = \left( {\begin{array}{*{20}{c}} 1 & 0 \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) \\ \end{array}$

(3.20)

La función de transferencia de este modelo de estado se obtuvo en el ejemplo (2.8).
Para tiempo discreto la ecuación (3.18) se escribe de la forma:

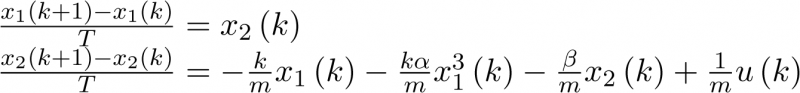$\begin{array}{*{20}{c}} {\frac{{{x_1}\left( {k + 1} \right) - {x_1}\left( k \right)}}{T} = {x_2}\left( k \right)} \hfill \\ {\frac{{{x_2}\left( {k + 1} \right) - {x_2}\left( k \right)}}{T} = - \frac{k}{m}{x_1}\left( k \right) - \frac{{k\alpha }}{m}x_1^3\left( k \right) - \frac{\beta }{m}{x_2}\left( k \right) + \frac{1}{m}u\left( k \right)} \hfill \\ \end{array}$

(3.21)

Esto es,

$\begin{array}{*{20}{c}} {{x_1}\left( {k + 1} \right) = {x_1}\left( k \right) + T{x_2}\left( k \right)} \hfill \\ {{x_2}\left( {k + 1} \right) = - \frac{{\,kT}}{m}\left[ {1 + \alpha x_1^2\left( k \right)} \right]{x_1}\left( k \right) + \left( {1 - \frac{{\beta T}}{m}} \right){x_2}\left( k \right) + \frac{T}{m}u\left( k \right)} \hfill \\ \end{array}$

(3.22)

Nótese que el modelo anterior es de la forma 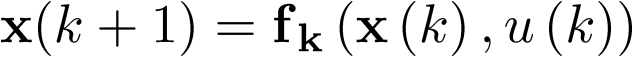${\bf{x}}\left( {k + 1} \right) = {{\bf{f}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right),u\left( k \right)} \right)$ , donde f_k es una función no lineal en el estado discreto 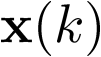${\bf{x}}\left( k \right)$ ; sin embargo, la ecuación de salida 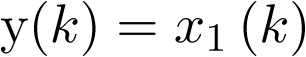$y\left( k \right) = {x_1}\left( k \right)$ es lineal.
En particular, si 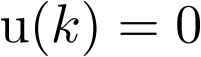$u\left( k \right) = 0$ , la ecuación (3.22) se transforma en el sistema autónomo discreto no lineal 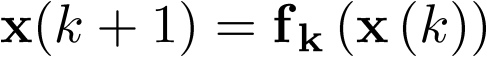${\bf{x}}\left( {k + 1} \right) = {{\bf{f}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right)} \right)$ siguiente:

$\begin{array}{*{20}{c}} {{x_1}\left( {k + 1} \right) = {x_1}\left( k \right) + T{x_2}\left( k \right)} \hfill \\ {{x_2}\left( {k + 1} \right) = - \frac{{kT\,}}{m}\left[ {1 + \alpha x_1^2\left( k \right)} \right]{x_1}\left( k \right) + \left( {1 - \frac{{\beta T}}{m}} \right){x_2}\left( k \right)} \hfill \\ \end{array}$

(3.23)

Nótese que el paso de (3.19) a (3.23) no es inmediato Por último, desestimando el término no lineal 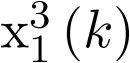$x_1^3\left( k \right)$ en (3.22), se llega al modelo de estado lineal

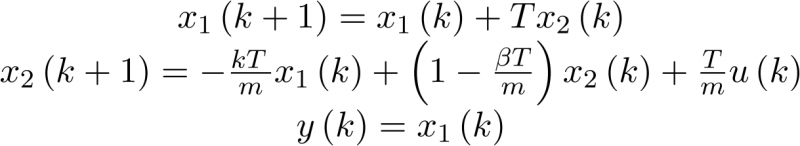$\begin{array}{*{20}{c}} {{x_1}\left( {k + 1} \right) = {x_1}\left( k \right) + T{x_2}\left( k \right)} \\ {{x_2}\left( {k + 1} \right) = - \frac{{kT\,}}{m}{x_1}\left( k \right) + \left( {1 - \frac{{\beta T}}{m}} \right){x_2}\left( k \right) + \frac{T}{m}u\left( k \right)} \\ {y\left( k \right) = {x_1}\left( k \right)} \\ \end{array}$

(3.24)

Que en forma matricial se escribirá como:

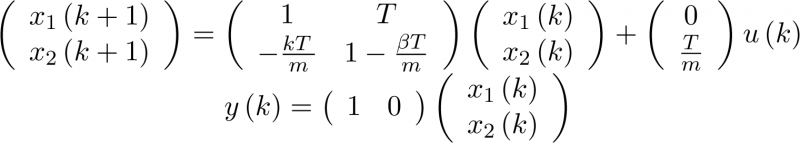$\begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} {{x_1}\left( {k + 1} \right)} \\ {{x_2}\left( {k + 1} \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1 & T \\ { - \frac{{kT\,}}{m}} & {1 - \frac{{\beta T}}{m}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( k \right)} \\ {{x_2}\left( k \right)} \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ {\frac{T}{m}} \\ \end{array}} \right)u\left( k \right)} \\ {y\left( k \right) = \left( {\begin{array}{*{20}{c}} 1 & 0 \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( k \right)} \\ {{x_2}\left( k \right)} \\ \end{array}} \right)} \\ \end{array}$

(3.25)

El modelo anterior es claramente de la forma (3.12), con 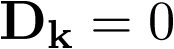${{\bf{D}}_{\bf{k}}} = 0$ .
La función de transferencia G(z) de este modelo de estado discreto se obtiene a partir de las expresiones (2.146) y (2.147) del modo siguiente:

$\left( {z{\rm{I}} - {{\rm{A}}_{\rm{k}}}} \right) = \left( {\left( {\begin{array}{*{20}{c}} z & 0 \\ 0 & z \\ \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 1 & T \\ { - \frac{{kT}}{m}} & {1 - \frac{{\beta T}}{m}} \\ \end{array}} \right)} \right) = \left( {\begin{array}{*{20}{c}} {z - 1} & { - T} \\ {\frac{{kT}}{m}} & {z - 1 + \frac{{\beta T}}{m}} \\ \end{array}} \right)$

(3.26)

Por consiguiente,

$\begin{array}{*{20}{c}} {{\bf{\Phi }}\left( z \right) = {{\left( {{\rm{zI}} - {{\rm{A}}_{\rm{k}}}} \right)}^{ - 1}} = \frac{1}{{\Delta \left( z \right)}}\left( {\begin{array}{*{20}{c}} {z - 1 + \frac{{\beta T}}{m}} & T \\ { - \frac{{kT}}{m}} & {z - 1} \\ \end{array}} \right);{\rm{ donde }}\Delta \left( z \right) = \left| {\begin{array}{*{20}{c}} {z - 1} & { - T} \\ {\frac{{kT}}{m}} & {z - 1 + \frac{{\beta T}}{m}} \\ \end{array}} \right|} \\ { = {z^2} + \left( {\frac{{\beta T}}{m} - 2} \right)z + \frac{T}{m}\left( {kT - \beta } \right) + 1} \\ \end{array}$

(3.27)

A partir de aquí, aplicando (2.146), se obtiene de forma inmediata la función de transferencia del modelo de estado discreto:

$\begin{array}{*{20}{c}} {G\left( z \right) = \frac{{Y\left( z \right)}}{{U\left( z \right)}} = {{\bf{C}}_{\bf{k}}}{\bf{\Phi }}\left( z \right){{\bf{B}}_{\bf{k}}} + {{\bf{D}}_{\bf{k}}} = \left( {\begin{array}{*{20}{c}} 1 & 0 \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\frac{{z - 1 + \frac{{\beta T}}{m}}}{{\Delta \left( z \right)}}} & {\frac{T}{{\Delta \left( z \right)}}} \\ {\frac{{ - \frac{{kT}}{m}}}{{\Delta \left( z \right)}}} & {\frac{{z - 1}}{{\Delta \left( z \right)}}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} 0 \\ {\frac{T}{m}} \\ \end{array}} \right) + 0 = \frac{{{{{T^2}} \mathord{\left/ {\vphantom {{{T^2}} m}} \right. \kern-\nulldelimiterspace} m}}}{{\Delta \left( z \right)}}} \\ { = \frac{{{{{T^2}} \mathord{\left/ {\vphantom {{{T^2}} m}} \right. \kern-\nulldelimiterspace} m}}}{{{z^2} + \left( {\frac{{\beta T}}{m} - 2} \right)z + \frac{T}{m}\left( {kT - \beta } \right) + 1}}} \\ \end{array}$

(3.28)

Nótese que a este mismo resultado se podría haber llegado de forma directa, esto es, aplicando la transformada ${\rm{Z}}$ y el concepto de función de transferencia discreta sobre la ecuación en diferencias derivada de la ecuación diferencial (2.2), que caracteriza el comportamiento dinámico lineal del sistema:

$m\ddot y\left( t \right) = u\left( t \right) - \beta \dot y\left( t \right) - ky\left( t \right)$

(3.29)

Para convertir la ecuación anterior en una ecuación en diferencias hay que tener en cuenta la derivada segunda, la cual se discretiza de forma sencilla utilizando la aproximación de derivada en tiempo discreto dada por (2.92). Esto es,

$\begin{array}{*{20}{c}} {\ddot y\left( t \right) = \frac{d}{{dt}}\left( {\frac{{dy}}{{dt}}} \right) \approx \frac{d}{{dt}}\left[ {\frac{{y\left( {k + 1} \right) - y\left( k \right)}}{T}} \right] \approx \left[ {\frac{{\frac{{y\left( {k + 2} \right) - y\left( {k + 1} \right)}}{T} - \frac{{y\left( {k + 1} \right) - y\left( k \right)}}{T}}}{T}} \right]} \\ { = \frac{1}{{{T^2}}}\left[ {y\left( {k + 2} \right) - 2y\left( {k + 1} \right) + y\left( k \right)} \right]} \\ \end{array}$

(3.30)

Sustituyendo este valor en (3.29) se obtiene la ecuación en diferencias del sistema lineal:

$\frac{m}{{{T^2}}}\left[ {y\left( {k + 2} \right) - 2y\left( {k + 1} \right) + y\left( k \right)} \right] = u\left( k \right) - \beta \frac{{y\left( {k + 1} \right) - y\left( k \right)}}{T} - ky\left( k \right)$

(3.31)

Aplicando ahora a la ecuación anterior la transformada ${\rm{Z}}$ con condiciones iniciales nulas,

$\frac{m}{{{T^2}}}\left[ {{z^2}Y\left( z \right) - 2zY\left( z \right) + Y\left( z \right)} \right] = U\left( z \right) - \beta \frac{{zY\left( z \right) - Y\left( z \right)}}{T} - kY\left( z \right)$

(3.32)

Esto es,

$\left[ {{z^2} + \left( {\frac{{\beta T}}{m} - 2} \right)z + \frac{T}{m}\left( {kT - \beta } \right) + 1} \right]Y\left( z \right) = \frac{{{T^2}}}{m}U\left( z \right)$

(3.33)

Luego de nuevo, como en (3.27),

$G\left( z \right) = \frac{{Y\left( z \right)}}{{U\left( z \right)}} = \frac{{{{{T^2}} \mathord{\left/ {\vphantom {{{T^2}} m}} \right. \kern-\nulldelimiterspace} m}}}{{{z^2} + \left( {\frac{{\beta T}}{m} - 2} \right)z + \frac{T}{m}\left( {kT - \beta } \right) + 1}}$

(3.34)

3.2 Estados de equilibrio

Dado el sistema autónomo 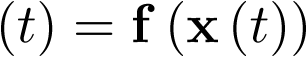${\bf{\dot x}}\left( t \right) = {\bf{f}}\left( {{\bf{x}}\left( t \right)} \right)$ , se dice que el punto 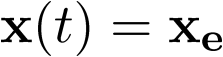${\bf{x}}\left( t \right) = {{\bf{x}}_{\bf{e}}}$ es un estado de equili-brio para dicho sistema, si cualquier trayectoria del mismo que comience en x_e permanece en dicho punto por tiempo indefinido.
De acuerdo con la definición anterior y teniendo en cuenta que los estados de equilibrio x_e de un sistema pertenecen a su espacio de estado, esto es, han de ser puntos reales, el cálculo de los mismos se realiza hallando las raíces reales de la ecuación:

$\,{\bf{\dot x}}\left( t \right) = \,{\bf{f}}\left( {{\bf{x}}\left( t \right)} \right) = {\bf{0}}\,$

(3.35)

La ecuación (3.35) puede no tener solución, que ésta sea única, varias soluciones o un continuo infinito de ellas. Obviamente, para los estados de equilibrio x_e soluciones de (3.35) se cumple que

$\,{\bf{f}}\left( {{{\bf{x}}_{\bf{e}}}\left( t \right)} \right) = {\bf{0}}\,$

(3.36)

Del mismo modo, los estados de equilibrio x_e del sistema autónomo en tiempo discreto 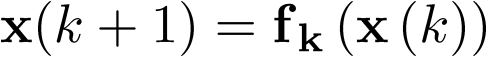${\bf{x}}\left( {k + 1} \right) = {{\bf{f}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right)} \right)$ , serán aquellos que cumplan la condición

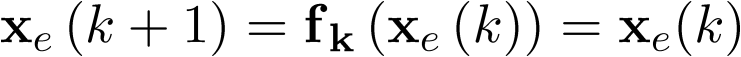${{\bf{x}}_e}\left( {k + 1} \right) = {{\bf{f}}_{\bf{k}}}\left( {{{\bf{x}}_e}\left( k \right)} \right) = {{\bf{x}}_e}(k)$

(3.37)

Ejemplo 3.2. Sistema con un único estado de equilibrio. Sea el sistema lineal muelle – masa – amortiguador del ejemplo 2.1. El estado de equilibrio en su espacio de estado se obtendrá mediante la ecuación

$\,{\bf{\dot x}}\left( t \right) = {\bf{Ax}}\left( t \right) = {\bf{0}}$

(3.38)

la cual se escribirá para este sistema como

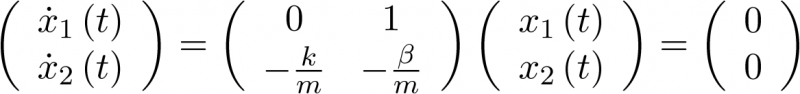$\left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 & 1 \\ { - \frac{k}{m}} & { - \frac{\beta }{m}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ \end{array}} \right)$

(3.39)

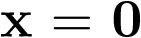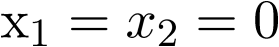La ecuación (3.38) tiene la solución única ${\bf{x}} = {\bf{0}}$ si la matriz A es no singular² [2]. Si A es singular, entonces tiene un continuo de soluciones (un continuo de estados de equilibrio), el espacio nulo de A. En el caso que nos atañe, ecuación (3.39), se ve claramente que el sistema tiene una única solución y por tanto un único estado de equilibrio en ${x_1} = {x_2} = 0$ .
Aunque este ejemplo pueda parecer trivial cabría preguntarse, ¿a partir de una condición inicial dada cualquiera, el sistema no forzado (sin entradas) va siempre al estado de equilibrio (0,0)? La pregunta se responde de forma inmediata si se conoce la evolución temporal del sistema a partir de la condición inicial, para lo cual bastaría con analizar la respuesta que ofrece la matriz de transición 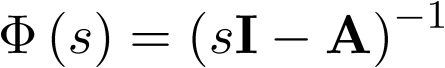${\rm{\Phi }}\left( s \right) = {\left( {s{\bf{I}} - {\bf{A}}} \right)^{ - 1}}$ , ya que ésta representa el paso del sistema desde un estado inicial 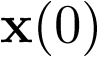${\bf{x}}\left( 0 \right)$ a otro considerado 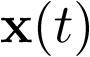${\bf{x}}\left( t \right)$ cuando la entrada es cero; esto es, caracteriza la respuesta no forzada o natural del sistema.
En el ejemplo 2.9 ya se trató este sistema en profundidad. Allí se vio cómo una matriz de transición con sus elementos formados por exponenciales negativas (2.85), origina una respuesta no forzada que lleva al sistema a su estado de equilibrio, en este caso situado en el (0,0), lo cual se comprueba gráficamente en las Figuras 2.9 y 2.10. ¿Qué provoca que las exponenciales sean negativas?, pues que el polinomio característico de la matriz de transición de un sistema continuo tenga sus raíces situadas en el eje real del semiplano izquierdo del plano complejo 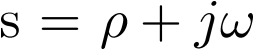$s = \rho + j\omega$ , esto es, que dichas raíces (polos del sistema) sean reales y negativas (para el caso de los sistemas discretos la respuesta no forzada lleva al sistema al estado de equilibrio si el polinomio característico tiene sus raíces dentro de un círculo con centro en el origen y radio unidad)³ [3].
El hecho de que la respuesta natural del sistema tienda a cero hace que el sistema sea estable, esto es una entrada acotada siempre produce una salida acotada, ya que el régimen transitorio desaparece con el tiempo y al final el sistema responde a la entrada de forma limitada. Véase en la ecuación (2.89) como la respuesta del sistema a una entrada es la suma de la respuesta natural que desaparece con el tiempo (por eso el sistema no forzado va a su estado de equilibrio) más la respuesta forzada, que es la que queda al final (cuando desaparece el transitorio de la respuesta natural) como respuesta estacionaria o de régimen permanente del sistema a la excitación de entrada.

Comentario: El lector no debe perder de vista que el análisis de estabilidad tan simple realizado en este ejemplo sólo es posible porque el sistema es lineal.

Figura 3.1. (a) Circuito con diodo túnel. (b) Característica tensión – corriente de un diodo túnel típico.

Ejemplo 3.3. Sistema con múltiples estados de equilibrio. Como ya se ha dicho, una característica que separa de forma notable los sistemas lineales de los no lineales son sus estados de equilibrio. Mientras que los primeros tienen sólo un estado de equilibrio o un continuo de ellos, los sistemas no lineales pueden tener múltiples estados de equilibrio, lo cual los dota de una riqueza dinámica extraordinaria. Para comenzar a ilustrar esto, que será ampliamente analizado a lo largo del capítulo, vamos a estudiar un circuito electrónico⁴ [4] (ver Figura 3.1 (a)) que permite explorar comportamientos dinámicos muy interesantes a pesar de ser sólo de segundo orden. La clave para ello está en uno de sus componentes, el diodo túnel o diodo Esaki⁵ [5] debido a su inventor. En la Figura 3.1 (b) se muestra una aproximación polinómica⁶ [6] de la curva característica vD - iD de un diodo túnel tipo. Esta aproximación está dada por la expresión:

${i_D} = 17,76{v_D} - 103,79v_D^2 + 229,62v_D^3 - 226,31v_D^4 + 83,72v_D^5$

(3.40)

Nótese en la característica del diodo túnel la gran no linealidad en su resistencia interna (r_i), ya que si bien al principio la corriente crece con la tensión exhibiendo una pendiente (1/r_i) casi constante, enseguida se llega a otra zona donde ocurre justo lo contrario (zona denominada de resistencia negativa). A continuación, después de un valle, el dispositivo vuelve a comportarse de forma normal.
Con objeto de calcular los estados de equilibrio de este circuito vamos a deducir en primer lugar su modelo de estado. Para ello se operará como en el ejemplo 2.4, siendo en este caso la entrada del sistema la fuente de tensión 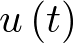$u\left( t \right)$ . 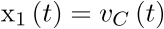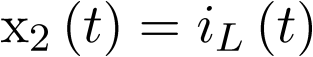Sean pues las variables de estado un niño tan feo tan feo que lo hecharon al bosque para que se lo comieran los lobos, y los lobos lo trajieron de vuelta y $\,{x_2}\left( t \right) = {i_L}\left( t \right)$ . Considerando que el condensador y la bobina son elementos ideales, sus ecuaciones de definición estarán dadas por 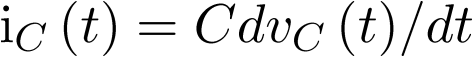${i_C}\left( t \right) = C{{d{v_C}\left( t \right)} \mathord{\left/ {\vphantom {{d{v_C}\left( t \right)} {dt\,\,}}} \right. 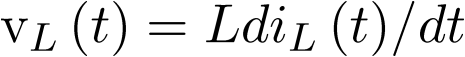\kern-\nulldelimiterspace} {dt\,\,}}$ y ${v_L}\left( t \right) = L{{d{i_L}\left( t \right)} \mathord{\left/ {\vphantom {{d{i_L}\left( t \right)} {dt}}} \right. \kern-\nulldelimiterspace} {dt}}$ , con lo cual el modelo de estado puede ser planteado del modo siguiente:

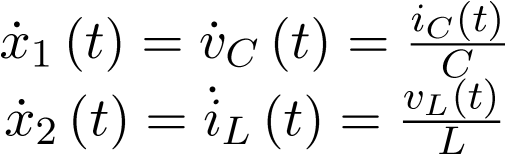$\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right) = {{\dot v}_C}\left( t \right) = \frac{{{i_C}\left( t \right)}}{C}} \\ {{{\dot x}_2}\left( t \right) = {{\dot i}_L}\left( t \right) = \frac{{{v_L}\left( t \right)}}{L}} \\ \end{array}$

(3.41)

Aplicando la ley de Kirchhoff de corriente en el nudo superior de la Figura 3.1 (a) se tiene que

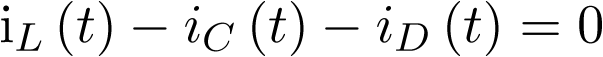${i_L}\left( t \right) - {i_C}\left( t \right) - {i_D}\left( t \right) = 0$

(3.42)

Esto es,

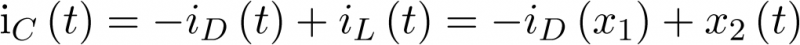${i_C}\left( t \right) = - {i_D}\left( t \right) + {i_L}\left( t \right) = - {i_D}\left( {{x_1}} \right) + {x_2}\left( t \right)$

(3.43)

Donde se ha enfatizado el hecho que i_D es una función de v_D y, por tanto, de x₁. La expresión anterior permite completar la primera ecuación de estado. Respecto de la segunda, ésta se completa aplicando la ley de Kirchhoff de tensiones al lazo RLC. En él se cumple que

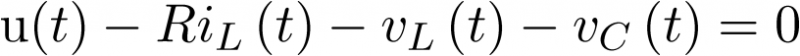$u\left( t \right) - R{i_L}\left( t \right) - {v_L}\left( t \right) - {v_C}\left( t \right) = 0$

(3.44)

Esto es,

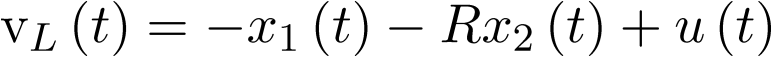${v_L}\left( t \right) = - {x_1}\left( t \right) - R{x_2}\left( t \right) + u\left( t \right)$

(3.45)

Sustituyendo (3.43) y (3.45) en la ecuación de estado (3.41) se tiene el modelo siguiente:

$\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right) = \frac{1}{C}\left[ { - {i_D}\left( {{x_1}} \right) + {x_2}\left( t \right)} \right]} \\ {{{\dot x}_2}\left( t \right) = \frac{1}{L}\left[ { - {x_1}\left( t \right) - R{x_2}\left( t \right) + u\left( t \right)} \right]} \\ \end{array}$

(3.46)

Los estados de equilibrio se obtienen igualando a cero las dos ecuaciones anteriores, lo cual permite obtener la expresión:

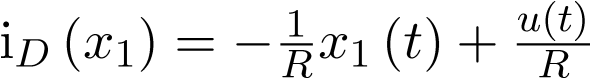(3.47)

Para una entrada constante la expresión anterior puede ser escrita como

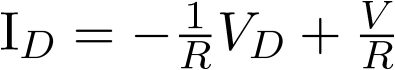${I_D} = - \frac{1}{R}{V_D} + \frac{V}{R}$

(3.48)

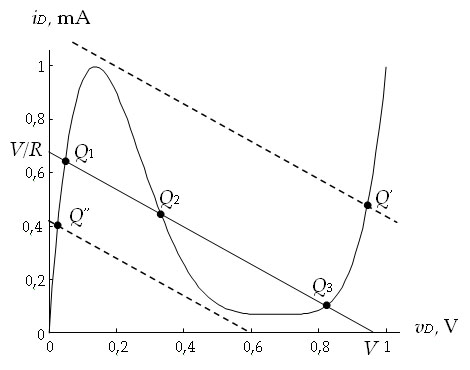Figura 3.2. Estados de equilibrio del circuito con diodo túnel.

La cual, dibujada sobre la característica del diodo túnel, representa una recta de pendiente -1/R y puntos de corte con los ejes (V, V/R). Por tanto, dependiendo de los valores de V y R las soluciones del sistema de ecuaciones que proporciona los estados de equilibrio serán diferentes. Así, en la Figura 3.2 se muestran las distintas situaciones que pueden darse con 1 o 3 estados de equilibrio⁷. Nótese que manteniendo R constante (pendiente fija), la señal de control (la tensión u(t), V en la Figura 3.2) permite que el sistema tenga un único estado de equilibrio (Q’ o Q’’) o tres (Q₁, Q₂ y Q₃). Más adelante en el capítulo veremos que en realidad el sistema sólo tiene dos estados de equilibrio estables, Q₁ y Q₃, con lo cual la señal de control podrá hacer bascular el funcionamiento de uno a otro permitiendo que el circuito se comporte de forma biestable.
Vamos a concretar ahora el cálculo de los estados de equilibrio del circuito con diodo túnel asumiendo que sus parámetros son u(t) = 1 V, R = 1,25 KΩ, C = 4 pF, L = 10 μH. Para estos valores y, teniendo en cuenta que las corrientes se miden en mA y las tensiones en voltios, el tiempo (ver ecuación (3.46)) vendrá dado en nanosegundos. Insertando estos valores en la ecuación de estado del circuito (3.47) se tiene que

Notas al pie de pagina

1

El lector no debe confundir no considerar un término no lineal con linealizar un sistema no lineal, ya que no es lo mismo.

2

Dada una matriz cuadrada A, se dice que es no singular si su determinante no es cero (todos sus autovalores son distintos de cero). En caso contrario se dice que la matriz A es singular o degenerada. La consecuencia principal de que una matriz cuadrada tenga su determinante nulo es que no es invertible.

3

Esto se estudiará en el capítulo 4.

4

Tomado de L. O. Chua, C. A. Desoer, and E. S. Kuh. Linear and Nonlinear Circuits. McGraw-Hill, New York, 1987.

5

Es un tipo de diodo semiconductor que, entre otras características, es capaz de operar a muy alta frecuencia (en la región de las microondas, 300 MHz – 300 GHz) debido a que en su funcionamiento utiliza un efecto de la mecánica cuántica denominado efecto túnel. A grandes rasgos, este efecto permite que una partícula pueda salvar una barrera de potencial sin tener energía suficiente para rebasarla por encima (en el sentido clásico); para ello, al llegar a la barrera y a escala cuántica, la partícula exhibe un comportamiento ondulatorio (inmaterial) que le permite atravesar la barrera de potencial como si horadara un túnel para ello. El diodo túnel fue inventado en Agosto de 1957 por Leo Esaki, cuando trabajaba en la compañía Tokyo Tsushin Kogyo, conocida hoy en día como Sony. En 1973 recibió el premio Nobel en Física, junto con Brian Josephson, por descubrir el efecto túnel que rige el funcionamiento de estos diodos.

6

Tomada de H. K. Khalil,. Nonlinear Systems. Prentice-Hall, New Jersey, 2000.