

A continuación se listan ejercicios de exámenes, resueltos o no, de las asignaturas Automática I y II.
Tenga en cuenta que estos ejercicios han podido ser enviados por cualquier usuario de la web, por lo que no sea crítico con los resultados (pueden contener errores). Edite el contenido si observa algún error.
Por favor, si resuelve algún ejercicio cámbiele el título, de forma que refleje que está resuelto (poner "Resuelto" al principio del título).
Si desea imprimirse todos los ejercicios de una sola vez, pulse en esta página "Versión para imprimir". Lo mismo puede hacer sobre la página anterior para obtener todos los apuntes de Automática I.
Para añadir nuevos ejercicios dele a "Añadir página hija".
Dados los siguientes lugares de las raíces, analice, sin realizar ningún cálculo, la respuesta temporal de los sistemas en lazo cerrado a los que representan, en función de la evolución del parámetro K. Comente cómo será el error de estado estacionario del sistema en lazo cerrado en cada caso, tanto si se someten a una estrada de tipo escalón como a una entrada de tipo rampa.
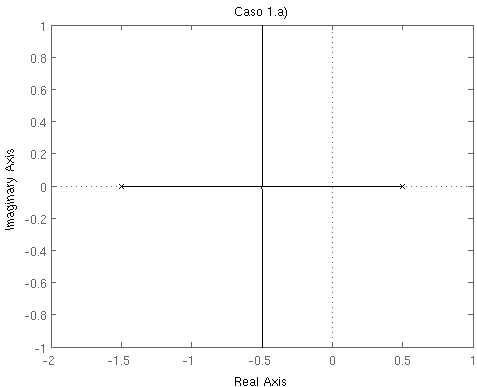
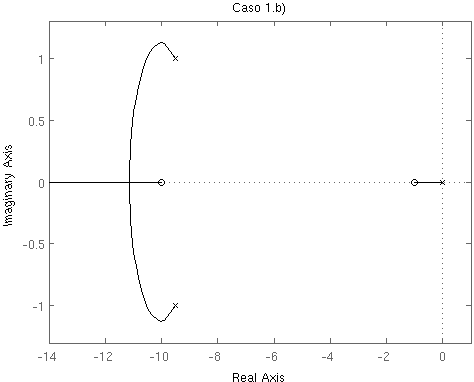
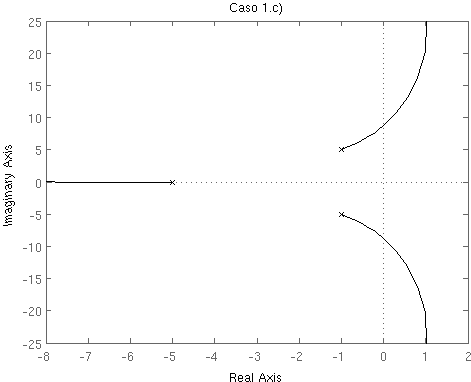
Trace manualmente el lugar de las raíces del siguiente sistema y coméntelo (estabilidad, respuesta transitoria, respuesta en régimen permanente, ...).
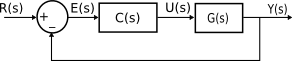 $C(s)=K$, $G(s)=\frac{(s+2)}{s(s+1)}$
$C(s)=K$, $G(s)=\frac{(s+2)}{s(s+1)}$
Una empresa le ha solicitado a última hora redactar un informe sobre la elección de un controlador para una de sus máquinas, el cual deberá estar listo a primera hora del día siguiente. Cuando se para a leer el encargo se da cuenta de que éste no dispone de información sobre la aplicación concreta a la que va a ser destinado el controlador, y le es imposible contactar con ninguno de los responsables de la empresa en cuestión.
El esquema de control a implantar se muestra en la siguiente figura, donde la función de transferencia de la planta es $G(s)=\frac{10}{s(s+5)}$, y los dos posibles controladores a aplicar son $C_1(s)=K_1$ y $C_2(s)=\frac{s+K_2}{s}$.

La única solución que le queda es redactar un informe lo más completo posible, para lo que seguirá el siguiente guión:
Determine si las siguientes afirmaciones son verdaderas o falsas, justificando su respuesta (se considerarán incorrectas las respuestas no justificadas o cuya justificación sea errónea).
Dado el sistema de control de la figura:
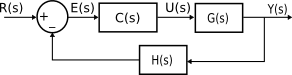
$G(s)=\frac{Y(s)}{U(s)}=\frac{1}{3s+1}$ $C(s)=\frac{U(s)}{E(s)}=\frac{K}{(s+1)}$ $H(s)=\frac{1}{(0.4s+1)}$
En la figura se puede observar el esquema simplificado de una planta hidroeléctrica. La electricidad es generada mediante la turbina al ser movida por el agua a presión que se evacua por el canal de desagüe de un embalse.
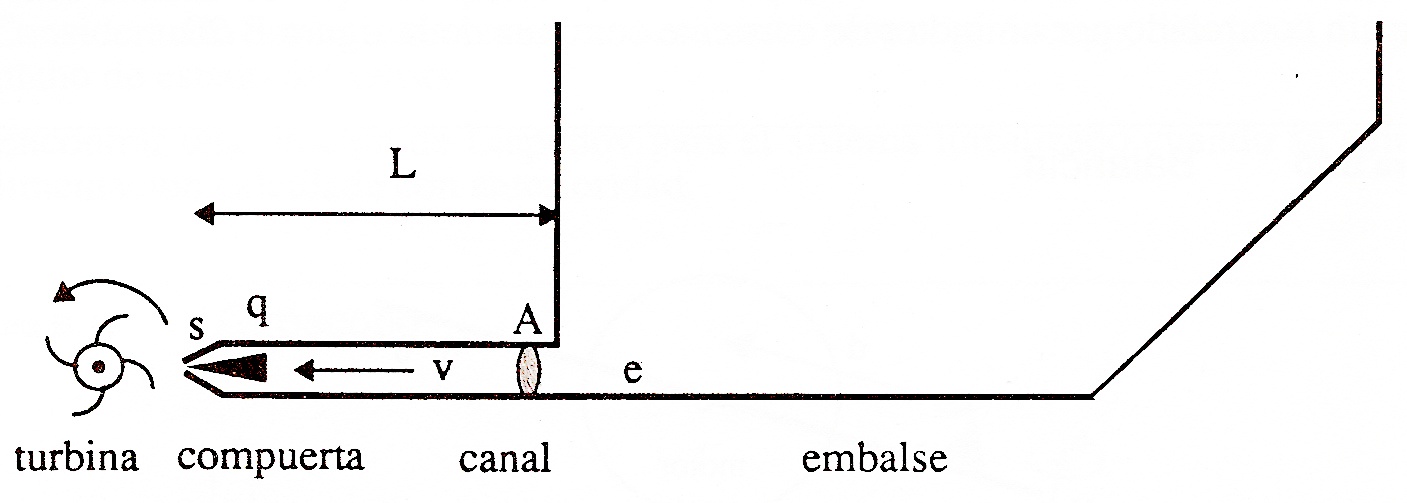
La potencia generada por la central es función de la velocidad con la circula el agua por el canal de acceso a la turbina, $v(t)$. Dicha velocidad viene determinada por la ecuación (1), donde $K_1$ y $K_2$ son constantes, $g$ es la aceleración de la gravedad, $L$ es la longitud del canal de desagüe, $e$ la presión a la entrada del canal, la cual se supone constante y $q(t)$ es la apertura de la compuerta del canal.
$$\dfrac{\text{d}v(t)}{\text{d}t} = \dfrac{K_2 \text{g}}{\text{L}}\left( e - K_1\dfrac{v(t)^2}{q(t)^2}\right) \quad\quad (1)$$
Nota: La ecuación (1) sólo tiene sentido para valores estrictamente positivos de $v(t)$ y $q(t)$.
Debido al tamaño de la compuerta, ésta tarda un tiempo en moverse desde que se le da la orden. Siendo $u(t)$ la señal de control del sistema (la orden para la compuerta), la dinámica de la apertura de la misma viene dada por la ecuación diferencial:
$$\dfrac{\text{d}q(t)}{\text{d}t} = 2 \left(u(t) - q(t)\right) \quad\quad (2)$$
Se solicita:
|
$${\small \mathbf{A} = \left.\left(\begin{array}{cccc} \dfrac{\partial f_1}{\partial x_1} & \dfrac{\partial f_1}{\partial x_2} & \cdots & \dfrac{\partial f_1}{\partial x_n}\\ \dfrac{\partial f_2}{\partial x_1} & \dfrac{\partial f_2}{\partial x_2} & \cdots & \dfrac{\partial f_2}{\partial x_n}\\ \cdots & \cdots & \ddots & \cdots\\ \dfrac{\partial f_n}{\partial x_1} & \dfrac{\partial f_n}{\partial x_2} & \cdots & \dfrac{\partial f_n}{\partial x_n}\\ \end{array}\right)\right|_{ \begin{array}{l} \mathbf{x}=\mathbf{x}_{eq}\\ \mathbf{u}=\mathbf{u}_{eq} \end{array} } }$$ |
$${\small \mathbf{B} = \left.\left(\begin{array}{cccc} \dfrac{\partial f_1}{\partial u_1} & \dfrac{\partial f_1}{\partial u_2} & \cdots & \dfrac{\partial f_1}{\partial u_m}\\ \dfrac{\partial f_2}{\partial u_1} & \dfrac{\partial f_2}{\partial u_2} & \cdots & \dfrac{\partial f_2}{\partial u_m}\\ \cdots & \cdots & \ddots & \cdots\\ \dfrac{\partial f_n}{\partial u_1} & \dfrac{\partial f_n}{\partial u_2} & \cdots & \dfrac{\partial f_n}{\partial u_m}\\ \end{array}\right)\right|_{ \begin{array}{l} \mathbf{x}=\mathbf{x}_{eq}\\ \mathbf{u}=\mathbf{u}_{eq} \end{array} } }$$ |
En la figura se puede observar el esquema simplificado de un sistema de levitación magnética similar al utilizado por los trenes de última tecnología. El campo magnético generado en la bobina a partir de la tensión de entrada $v(t)$, provoca la elevación de la bola de metal de masa m, de forma que controlando adecuadamente la tensión de entrada puede mantenerse suspendida la masa a una distancia $l(t)$ determinada. Dado el conjunto de ecuaciones que gobierna la dinámica del sistema, se desea estudiar el comportamiento del mismo, para lo cual se solicita:
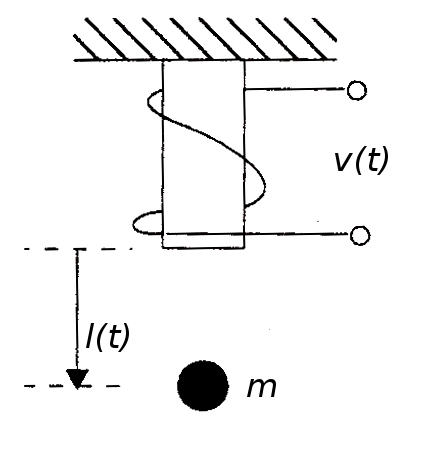 |
$m \dfrac{\text{d}^2 l(t)}{\text{d} t^2} = m g - \dfrac{i(t)^2}{l(t)}$
Masa → $m = 0.01 kg$ |
|
$${\small \mathbf{A} = \left.\left(\begin{array}{cccc} \dfrac{\partial f_1}{\partial x_1} & \dfrac{\partial f_1}{\partial x_2} & \cdots & \dfrac{\partial f_1}{\partial x_n}\\ \dfrac{\partial f_2}{\partial x_1} & \dfrac{\partial f_2}{\partial x_2} & \cdots & \dfrac{\partial f_2}{\partial x_n}\\ \cdots & \cdots & \ddots & \cdots\\ \dfrac{\partial f_n}{\partial x_1} & \dfrac{\partial f_n}{\partial x_2} & \cdots & \dfrac{\partial f_n}{\partial x_n}\\ \end{array}\right)\right|_{ \begin{array}{l} \mathbf{x}=\mathbf{x}_{eq}\\ \mathbf{u}=\mathbf{u}_{eq} \end{array} } }$$ |
$${\small \mathbf{B} = \left.\left(\begin{array}{cccc} \dfrac{\partial f_1}{\partial u_1} & \dfrac{\partial f_1}{\partial u_2} & \cdots & \dfrac{\partial f_1}{\partial u_m}\\ \dfrac{\partial f_2}{\partial u_1} & \dfrac{\partial f_2}{\partial u_2} & \cdots & \dfrac{\partial f_2}{\partial u_m}\\ \cdots & \cdots & \ddots & \cdots\\ \dfrac{\partial f_n}{\partial u_1} & \dfrac{\partial f_n}{\partial u_2} & \cdots & \dfrac{\partial f_n}{\partial u_m}\\ \end{array}\right)\right|_{ \begin{array}{l} \mathbf{x}=\mathbf{x}_{eq}\\ \mathbf{u}=\mathbf{u}_{eq} \end{array} } }$$ |
Ejercicio 1 (3 puntos). El sistema de suspensión de un automóvil mostrado en la figura puede ser modelado mediante la siguiente ecuación diferencial:
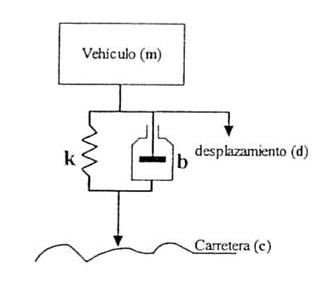 $m \ddot{d}+b(\dot{d}-\dot{c})+k(d-c)=0$
$m \ddot{d}+b(\dot{d}-\dot{c})+k(d-c)=0$
donde d es el desplazamiento vertical del vehículo, m su masa, b es el coeficiente de fricción viscosa del amortiguador y k la constante del muelle. El desplazamiento provocado por el perfil de la carretera (c) se considera como la señal de entrada del mismo.
Se desea obtener:
a) (1 Punto). La función de transferencia del sistema D(s)/C(s).
b) (2 Puntos). Un modelo de estados del sistema mediante la utilización de un diagrama de flujo de señal de éste.
SOLUCIÓN:
a) Aplicamos Laplace a la ecuación del sistema para trabajar en el dominio de s y nos queda:
$ms^2 D(s) + b(sD(s) - sC(s)) + k(D(s) - C(s)) = 0$ ; sacamos factor común en D(s) y C(s):
$D(s)(ms^2 + bs + k) - C(s)(bs + k) = 0$ ; Finalmente, despejando D(s)/C(s), obtenemos la función de transferencia del sistema:
$\dfrac{{D(s)}}{{C(s)}} = \dfrac{{bs + k}}{{ms^2 + bs + k}}$
b) Para obtener el diagrama de flujo de señal del sistema, debemos sacar los caminos directos y los lazos.
Fórmula de Mason, para obtener el diagrama de flujo por comparación:
$G = \dfrac{\sum\limits _k \left( P_k - \Delta _k \right)}{\Delta}$
$\dfrac{{D(s)}}{{C(s)}} = \dfrac{{bs + k}}{{ms^2 + bs + k}}\cdot\dfrac{{\dfrac{{s^{ - 2} }}{m}}}{{\dfrac{{s^{ - 2} }}{m}}} = \dfrac{{\dfrac{{bs^{ - 1} }}{m} + \dfrac{{ks^{ - 2} }}{m}}}{{1 + \dfrac{{bs^{ - 1} }}{m} + \dfrac{{ks^{ - 2} }}{m}}}$
Caminos directos:
$P_1 = \dfrac{k}{m}s^{ - 2}$
$P_2 = \dfrac{b}{m}s^{ - 1}$
Lazos:
$L_1 = \dfrac{{ - b}}{m}s^{ - 1}$
$L_2 = \dfrac{{ - k}}{m}s^{ - 2}$
Una vez obtenido los caminos directos y los lazos, realizamos el diagrama de flujo de señal del sistema que se muestra a continuación:
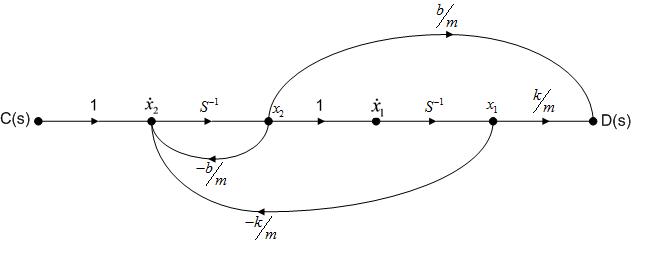
Como podemos ver en el diagrama, las dos condiciones que ha de cumplir éste, se cumplen:
-Todos los lazos tienen en común al menos un nodo.
-Todos los caminos directos tienen en común con todos los lazos, al menos, un nodo.
Finalmente, utilizando el diagrama de flujo de señal del sistema, obtenemos el modelo de estados de dicho sistema:
$\left( \begin{array}{l}
\dot x _1 \\
\dot x _2 \\
\end{array} \right) = \left( {\begin{array}{*{20}c}
0 & 1 \\
{\dfrac{{ - k}}{m}} & {\dfrac{{ - b}}{m}} \\
\end{array}} \right)\left( \begin{array}{l}
x_1 \\
x_2 \\
\end{array} \right) + \left( \begin{array}{l}
0 \\
1 \\
\end{array} \right)c(t)$
$d(t) = \left( {\begin{array}{*{20}c}
{\dfrac{k}{m}} & {\dfrac{b}{m}} \\
\end{array}} \right)\left( {\begin{array}{*{20}c}
{x_1 } \\
{x_2 } \\
\end{array}} \right) + \left( 0 \right)c(t)$
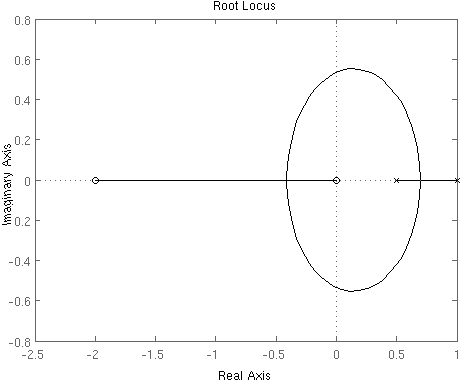
Ejercicio 3 (3 Puntos). Trace manualmente el lugar de las raíces del siguiente sistema:

Recuerde: roots le permite obtener las raíces de una ecuación.
SOLUCIÓN:
La ecuación característica del sistema es la siguiente:
$EC \equiv 1 + kP(s) = 0$ donde $P(s) = \dfrac{{s + 2}}{{s(s + 1)}}$
El Lugar de las Raíces comienza siempre en los polos de lazo abierto, con k=0, y termina en los ceros, con k=$\infty$. Tendrá tantas Ramas como polos de P(s), y éstas llegarán a los ceros de P(s) ó,si no los hay finitos, fugarán a infinito. A continuación procedemos a obtener los datos necesarios para trazar el Lugar de las Raíces de forma aproximada.
- Polos y ceros:
Conociendo P(s), podemos saber el números de polos (n) y el número de ceros (m), así como el valor de cada polo y de cada cero.
$P(s) = \dfrac{{s + 2}}{{s(s + 1)}}$
Vemos en la ecuación que existen dos polos y un cero:
n=2 ; p1=0 ; p2=-1
m=1 ; z=-2
Con estos datos, ya podemos comenzar a realizar la gráfica que muestra el Lugar de las Raíces, de momento tenemos lo siguiente:
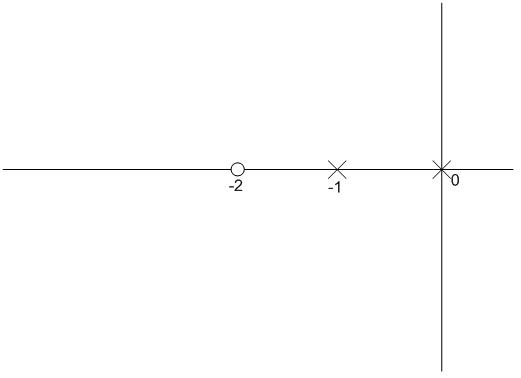
Al tener dos polos y un cero, ya sabemos que debe haber una rama que fugará a infinito.
- Lugar de las Raíces en el Eje Real:
El Lugar de las Raices existe en el eje real en cualquier segmento para el que el número total de polos y ceros de P(s) a la derecha es impar. Por tanto, existirá Lugar de las Raíces en el eje real en los intervalos:
$\sigma \in \left\{ {\left( { - \infty , - 2} \right] \cup \left[ { - 1,0} \right]} \right\}$
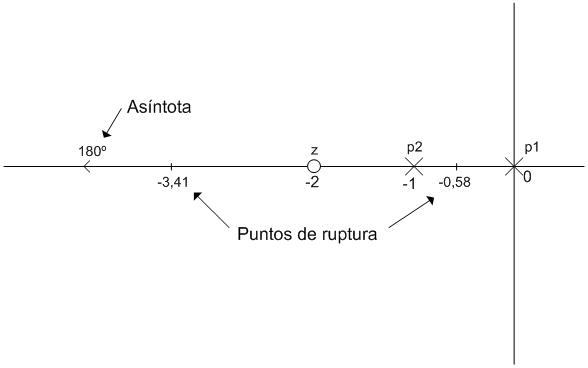
- Asíntotas:
Debemos calcular una asíntota, ya que una rama fugará a infinito.
k=0,...,n-m-1 ; n-m-1=2-1-1=0 ; k=0
$\sigma _k = \dfrac{{180 + k360}}{{n - m}}$
$\sigma _0 = \dfrac{{180}}{{2 - 1}} = 180{\rm{ grados}}$
El punto de corte de la asíntota con el eje real se calcularía así, aunque no tiene sentido con una sola asíntota):
$\sigma _C = \dfrac{{\sum {polos} - \sum {ceros} }}{{n - m}} = \dfrac{{(0 - 1) - ( - 2)}}{{2 - 1}} = 1$
El ángulo que forma la asíntota con el eje real es de 180º, y el punto de corte entre ambos es en 1.
- Puntos de ruptura:
Los puntos de ruptura son los valores reales de 's' que satisfacen:
$\dfrac{d}{{ds}}P(s) = 0$
$\dfrac{d}{{ds}}\left( {\dfrac{{s + 2}}{{s^2 + s}}} \right) = \dfrac{{s^2 + s - (s + 2)(2s + 1)}}{{\rlap{--} d\rlap{--} \rlap{--} e\rlap{--} n^2 }} = 0$
$\dfrac{d}{{ds}}P(s) = s^2 + 4s + 2 = 0$
Obtenemos las raíces con ayuda de matlab: roots([1 4 2])
$s_1 = - 3,41$
$s_2 = - 0,58$
Seguimos completando la gráfica que muestra el Lugar de las Raíces:
- Cortes con el eje imaginario:
Los cortes con el eje imaginario serán aquellos valores imaginarios puros de 's' pertenecientes al Lugar de las Raíces. Para calcularlos emplearemos el Criterio de Routh. También debemos obtener la ecuación característica (EC).
$EC \equiv 1 + kP(s) = 1 + k\dfrac{{(s + 2)}}{{s(s + 1)}} = 0$
$EC \equiv s(s + 1) + k(s + 2) = s^2 + s(k + 1) + 2k = 0$
Aplicamos el Criterio de Routh:
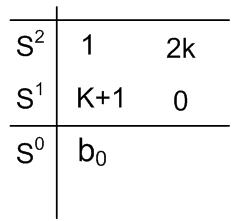
$b_0 = \dfrac{{ - 1}}{{k + 1}}\left| {\begin{array}{*{20}c}
1 & {2k} \\
{k + 1} & 0 \\
\end{array}} \right| = \dfrac{{ - 1( - 2k(k + 1))}}{{k + 1}} = 2k$
${\rm{2k = 0 }} \to {\rm{k = 0}} \to (k + 1)s = 0 \to s = 0$
Por tanto existe un corte con el eje imaginario cuando k=0 que se produce en el punto s=0 (ya se sabía puesto que es un polo en lazo abierto).
Finalmente, el Lugar de las Raíces del sistema nos queda aproximadamente de la siguiente forma:
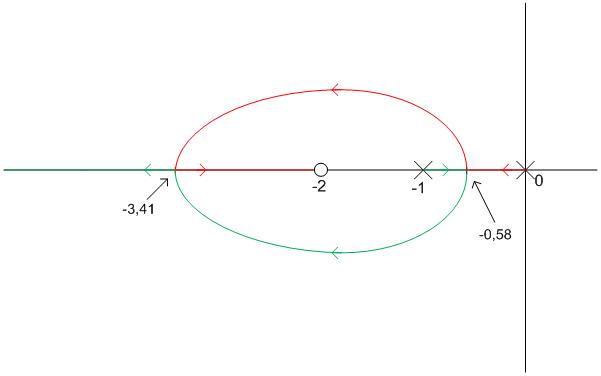
Podemos ver de forma aproximada el recorrido de cada polo a menudo que aumenta k desde cero hasta infinito. Uno de ellos fuga a infinito por la asíntota de 180º y otro fuga al cero z=-2.
Estudio dinámico del sistema conforme k aumenta de 0 a $\infty$:
Cuando k=0, el sistema es marginalmente estable. En el momento en que k deja de valer cero (el sistema se hace estable para k>0), el polo que inicialmente estaba en 0 (p1) se mueve hacia la izquierda, por tanto disminuye el tiempo de asentamiento ya que el sistema es más rápido al alejarse del origen dicho polo, y el polo que inicialmente estaba en -1 (p2) se mueve hacia la derecha, en este momento el sistema es sobreamortiguado por tener los dos polos reales y distintos. Conforme aumenta k sigue moviéndose cada polo en la dirección citada hasta que coinciden en el punto de ruptura (-0,58), donde el sistema es críticamente amortiguado por tener los dos polos reales e iguales. Sigue aumentando k y cada polo se va por una rama, el sistema será aun más rápido por estar alejándose los dos polos del origen y existe sobreimpulso en el sistema, éste será subamortiguado por tener los dos polos complejos conjugados hasta el momento en que coincidan éstos de nuevo en el otro punto de ruptura (-3,41), donde el sistema será de nuevo críticamente amortiguado. A partir de aqui un polo fugará a infinito por la asíntota de 180º, y otro, el dominante, fugará al cero (z=-2), en este intervalo no hay sobreimpulso y el sistema irá siendo más lento conforme aumenta k.
Estudio estático del sistema:
El sistema en lazo abierto tiene un polo en el origen (p1), es decir, es de tipo 1. Por tanto el error de tipo escalón será nulo, el error de tipo rampa será constante y el error de tipo hipérbola será infinito.
Se desea diseñar el sistema de control de la figura. Teniendo en cuenta las características propias de la aplicación, se ha optado por diseñar un sistema de control exento de error de posición y con un error de velocidad menor del 10%. El tiempo de asentamiento deberá ser inferior a 1 segundo, y el sobreimpulso máximo admitido es del 5%.
 $C(s)=K_1$, $G(s)=\dfrac{1}{(s^2+3s)}$ y $H(s)=K_2s+1$
$C(s)=K_1$, $G(s)=\dfrac{1}{(s^2+3s)}$ y $H(s)=K_2s+1$
Resolución:
Los requerimientos del diseño son:
Error de posición --> ess (pos) = 0 (exento de error de posición ).
Error de velocidad --> ess (vel) < 10%
Tiempo de establecimiento --> ts (2%) < 1 seg
Sobreimpulso --> Mp< 5%
En primer lugar vemos de que tipo es el sistema calculando su FT de lazo abierto, que es:
$ FT = C(s) G(s) H(s) = K_1 \dfrac{1}{{(s^2 + 3s)}} (K_2 s + 1) = \dfrac{{K_1 K_2 s + K_1 }}{{s(s + 3)}}$ Vemos que es de tipo 1, por lo que el ess (pos) será cero, por lo que no hace falta calcularlo.
Para calcular el ess(vel) lo haremos de dos modos: uno usando la expresión del error de realimentación, y otro usando el error real.
$ \left. \begin{array}{l}
\mu (s) = Y(s) H(s) \\
E(s) = R(s) - \mu (s) \\
Y(s) = E(s) C(s) G(s) \\
\end{array} \right\}E(s) = R(s) - E(s) C(s) G(s) H(s){\rm{ }} \Rightarrow $
$ \Rightarrow {\rm{ }}E(s) = R(s)\dfrac{1}{{1 + C(s) G(s) H(s)}} = R(s)\dfrac{{s(s + 3)}}{{s(s + 3) + K_1 (1 + K_2 s)}}$
Ahora aplicamos el teorema del valor final con una señal de entrada rampa R(s)=1/s2:
$ e_{ss} (vel) = \lim \limits _{x \to 0} s E(s) = \lim \limits_{x \to 0} s R(s)\dfrac{s(s + 3)}{s(s + 3) + K_1 (1 + K_2 s)} = $
$ = \lim \limits_{x \to 0} s \dfrac{1}{s^2} \dfrac{s(s + 3)}{s(s + 3) + K_1 (1 + K_2 s)} = \dfrac{3}{K_1 (1 + 0)} = \dfrac{3}{K_1 }$
Sabemos que uno de los requisitos que tiene que cumplir es que ess (vel)< 10%, por tanto:
$ \dfrac{3}{{K_1 }} < 0,1{\rm{ }} \Rightarrow {\rm{ }}K_1 > \dfrac{3}{{0,1}}{\rm{ }} \Rightarrow {\rm{ }}K_1 > 30$
Calculamos la FT de lazo cerrado:
$ FTLC = \dfrac{Y(s)}{R(s)} = \dfrac{C(s) G(s)}{1 + C(s) G(s) H(s)} = \dfrac{K_1 \dfrac{1}{(s^2 + 3s)}}{1 + K_1 \dfrac{1}{(s^2 + 3s)}(K_2 s + 1)} = $
$ = \dfrac{K_1 }{s(s + 3) + K_1(1 + K_2 s)} = \dfrac{K_1 }{s^2 + (3 + K_1K_2 )s + K_1}$
AVISO: La comparación del sistema resultante con un sistema de orden 2 es sólo válida cuando puede realizarse, es decir, cuando el sistema resultante también es de orden 2 o tiene 2 polos dominantes. Sin embargo, en la mayoría de los casos esto no es así. Para esos casos donde la comparación no es posible, es necesario trazar el Lugar Geométrico de la Raíces del sistemas y así, mediante su análisis, saber cómo se comportará en función del parámetro a diseñar.
Comprobamos que el sistema es de 2º orden, por lo que el sobreimpulso será:
$ Mp = e^{\dfrac{ - \delta \pi }{\sqrt {1 - \delta ^2 }}}$
De esta expresión despejaremos el coeficiente de amortiguamiento $\delta$, quedando:
$ \delta = \sqrt {\dfrac{\ln ^2 Mp}{\pi + \ln ^2 Mp}} = \sqrt {\dfrac{\ln ^2 0,05}{\pi + \ln ^2 0,05}} = 0,69$
Como Mp debe ser menor del 5%, observamos como cambian los polos al variar $\delta$ en los dos casos, que son:
$ p_{1,2} = - \delta \omega _n \pm j\omega _n \sqrt {1 - \delta ^2 } \left\{ \begin{array}{l}
\delta \text{tiende a 0} \Rightarrow p_{1,2} = \pm j\omega _n \sqrt {1 - \delta ^2 } \Rightarrow \text{Oscila y aumenta Mp} \\
\delta \text{tiende a 1} \Rightarrow p_{1,2} = - \omega _n \Rightarrow \text{Mp tiende a 0} \\
\end{array} \right.$
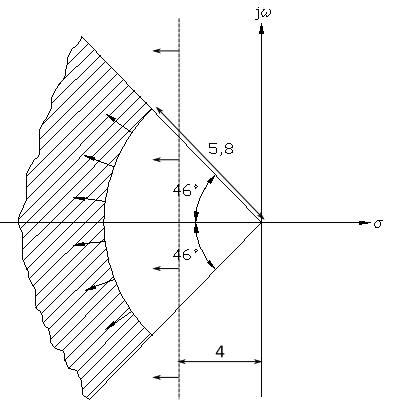
Por tanto, $\mathbf{\delta > 0.69}$.
El tiempo de establecimiento en los sistemas de 2º orden para un rango del 2% es:
$ t_s (2\% ) = \dfrac{4}{{\delta \omega _n }} < 1{\rm{ seg}}$
De donde podemos despejar la frecuencia natural no amortiguada ωn:
$ \omega _n > \dfrac{4}{{\delta t_s }} = \dfrac{4}{{0,69 · 1}} = 5,8{\rm{ }}rad/s$
Puesto que:
$ \cos \beta = \delta = 0,69{\rm{ }} \Rightarrow {\rm{ }}\beta {\rm{ = arcos 0}}{\rm{,69 = 46}}{\rm{,37}}^ \circ$
Como δ>0,69 esta aumenta , lo que hace que p1,2 tiendan a ser más reales, y por tanto β menor. Así que β < 46,37º.
Obtenemos la parte real de los polos a partir de la expresión de ts:
$ \dfrac{4}{{\delta \omega _n }} < 1{\rm{ }} \Rightarrow {\rm{ }}\delta \omega _n > 4{\rm{ }} \Rightarrow {\rm{ - }}\delta \omega _n < - 4$
Los polos de lazo cerrado en el plano S se dibujarán como:
Por último, obtendremos la expresión para K2 comparando la FTLC con la expresión modelo de un sistema de 2º orden, debiéndose cumplir las inecuaciones anteriores.
$ \dfrac{{K_1 }}{{s^2 + (3 + K{}_1K_2 )s + K_1 }} = \dfrac{{K_0 \omega _n^2 }}{{s^2 + 2\delta \omega _n s + \omega _n^2 }}$
La frecuencia natural no amortiguada será:
$ \omega _n^2 = K_1 {\rm{ }}{\rm{, }}\omega _n^{} = \sqrt {K_1 } \Rightarrow {\rm{ }}\omega _n^{} > \sqrt {30} = 5,48{\rm{ }}rad/s$
Al ser este valor menor que antes es menos restrictivo, por lo que nos quedamos con el anterior para el diseño, siendo el requisito:
$ K_1 {\rm{ = }}\omega _n^2 {\rm{ }} = 5,8^2 {\rm{ = 33}}{\rm{,64 }} \Rightarrow {\rm{ }}K_1 > 33,64$
Y la expresión para el coef. de amortiguamiento $\delta$ será:
$ \delta = \dfrac{{3 + K_1 K_2 }}{{2\omega _n }}$
A continuación escogeremos valores para K1 y K2. Para ello tendremos en cuenta que se cumplan los requisitos calculados K1>33,64 y δ>0,69.
Obtenemos un valor de K2 sustituyendo estos valores en la última expresión que hemos obtenido y despejando:
$ K_2 = \dfrac{{2\delta \sqrt {K_1 } - 3}}{{K_1 }} = \dfrac{{2 · 0,69\sqrt {33,64} - 3}}{{33,64}} = 0,148{\rm{ }} \Rightarrow {\rm{ }}K_2 > 0,148$
Con esto, y dando un valor a K1 y a K2 que no estén muy lejos de los límites calculados pero tampoco demasiado cerca (p.ej. K1=35 y K2=0,18) obtenemos δ, que será:
$ \delta = \dfrac{{3 + K_1 K_2 }}{{2\omega _n }} = \dfrac{{3 + 35 · 0,18}}{{2\sqrt {35} }} = 0,78$
Comprobamos que cumple el requisito de diseño.
Y el sobreimpulso será:
$ Mp = e^{\dfrac{{ - \delta \pi }}{{\sqrt {1 - \delta ^2 } }}} = e^{\dfrac{{ - 0,78\pi }}{{\sqrt {1 - 0,78^2 } }}} = 0,02{\rm{ }}(2\% )$
Nota: Este apartado no era necesario calcularlo en el examen.
$ \left. \begin{array}{l}
E'(s) = R(s) - Y(s) \\
FTLC = \dfrac{{Y(s)}}{{R(s)}} = \dfrac{{K_1 }}{{s^2 + (3 + K{}_1K_2 )s + K_1 }} \\
\end{array} \right\}E'(s) = R(s){\rm{ }}\left( {{\rm{1 - }}\dfrac{{K_1 }}{{s^2 + (3 + K{}_1K_2 )s + K_1 }}} \right) \Rightarrow $
$ \Rightarrow {\rm{ }}E'(s) = R(s)\left( {\dfrac{{s(s + 3 + K_1 K_2 )}}{{s^2 + s(3 + K_1 K_2 ) + K_1 }}} \right)$
Ahora aplicamos el teorema del valor final con una señal de entrada rampa R(s)=1/s2:
$e_{ss} (vel) = \lim \limits_{x \to 0} s E'(s) = \lim \limits_{x \to 0} s R(s)\dfrac{s(s + 3 + K_1 K_2 )}{s^2 + s(3 + K_1 K_2 ) + K_1 } = $
$ = \lim \limits_{x \to 0} s \dfrac{1}{s^2 } \dfrac{s(s + 3 + K_1 K_2 )}{s^2 + s(3 + K_1 K_2 ) + K_1 } = \dfrac{3 + K_1 K_2 }{K_1} = \dfrac{3}{K_1 } + K_2$
Sabemos que uno de los requisitos que tiene que cumplir es que ess (vel)< 10%, por tanto:
$ \dfrac{3}{{K_1 }} + K_2 < 0,1{\rm{ }} \Rightarrow {\rm{ }}K_1 > \dfrac{3}{{0,1 - K_2 }}{\rm{ }}{\rm{, }}K_2 < \dfrac{{0,1K_1 - 3}}{{K_1 }}$
Al igual que antes, en principio los requisitos serán δ>0,69 (por tanto β<46,37º).
A continuación escogeremos valores para K1 y K2. Para ello tendremos en cuenta que se cumplan los requisitos calculados $ K_1 > \dfrac{3}{{0,1 - K_2 }}{\rm{ }}{\rm{, }}K_2 < \dfrac{{0,1K_1 - 3}}{{K_1 }}{\rm{ }}y{\rm{ }}\delta > 0,69$.
Obtenemos un valor de K2 dando un valor a K1 adecuado (p.ej., el de antes K1=35) y sustituyendo estos valores en las expresiones que hemos obtenido antes:
$ K_2 < \dfrac{{0,1K_1 - 3}}{{K_1 }} = \dfrac{{0,1 · 35 - 3}}{{35}} = 0,0142{\rm{ }} \Rightarrow {\rm{ }}K_2 < 0,0142$
$ K_2 < \dfrac{{2\delta \sqrt {K_1 } - 3}}{{K_1 }} = \dfrac{{2 · 0,69\sqrt {35} - 3}}{{35}} = 0,147{\rm{ }} \Rightarrow {\rm{ }}K_2 < 0,147$
El primero es más restrictivo, por lo que damos un valor a K2 que no esté muy lejos de este límite pero tampoco demasiado cerca (p.ej. K2=0,01).
Comprobamos los resultados obtenidos en los dos modos de hacer el ejercicio mediante simulación en Matlab.
El código que genera todas las simulaciones es:
clc, clear all, close all
K1=35;
K2=0.18;
G=tf(1,[1,3,0]);
H=tf([K2,1],1);
S=feedback(K1*G,H); %FT= Y(s)/R(s)
%Simulacion frente a entrada ESCALON (Solo para comprobar que es casi cero)
t=0:1e-3:3;
figure
[y,t]=step(S,t);
u=ones(size(t)); %Escalon
ess_pos=u(end)-y(end) %error de posicion
plot(t,y,t,u,'r--'), xlabel('Tiempo (s)'), ylabel('Escalon')
%Simulacion frente a entrada RAMPA (unitaria)
r=t; %Funcion rampa unitaria
%Modo 1: Error de realimetacion
E_REALIM=tf([1,3,0],[1,3+K1*K2,K1]);
[e_vel,t]=lsim(E_REALIM,r,t);
figure,plot(t,e_vel), xlabel('Tiempo (s)'), ylabel('Error de realimentacion')
ess_vel_realim=e_vel(end) %error de velocidad de realimentacion
ess_vel_realim_teorico=3/K1 %error de velocidad de realimentacion teorico
%Modo 1: Error real
K1=35;
K2=0.01;
G=tf(1,[1,3,0]);
H=tf([K2,1],1);
S=feedback(K1*G,H); %FT= Y(s)/R(s)
r=t; %Funcion rampa unitaria
[y2,t]=lsim(S,r,t);
ess_vel_real=r(end)-y2(end) %error de velocidad real
ess_vel_real_teorico=(3/K1)+K2 %error de velocidad real teorico
figure,plot(t,y2,t,r,'r--'), xlabel('Tiempo (s)'), ylabel('Rampa')
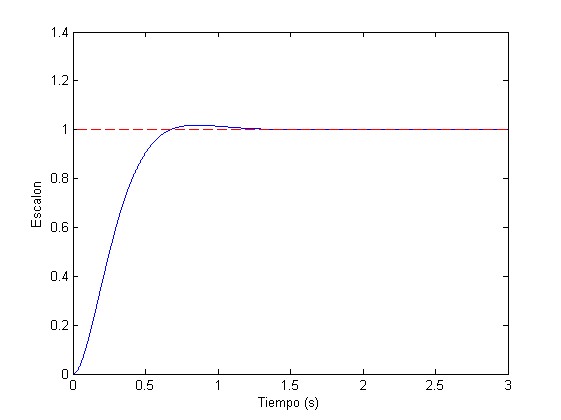
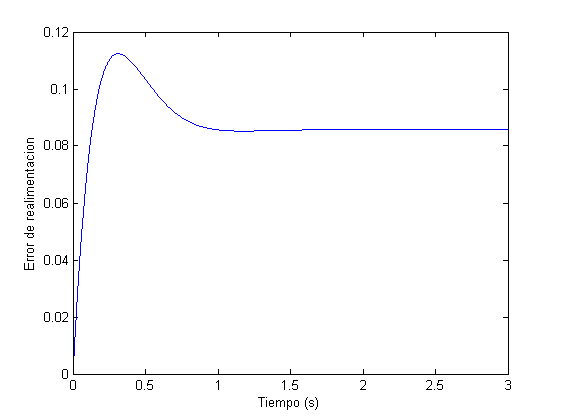
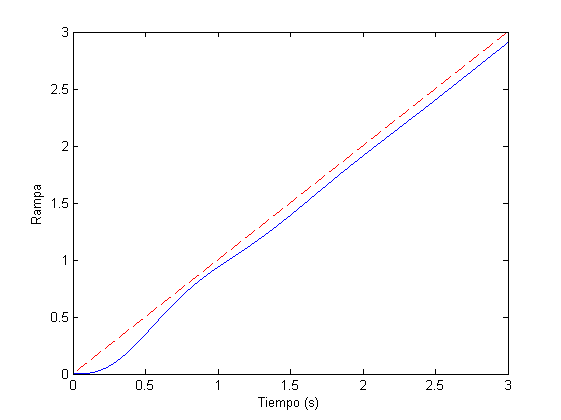
Como puede observarse, tanto en los resultados de la consola como en las representaciones gráficas, se cumplen las condiciones del diseño. Las pequeñas diferencias existentes entre los errores teóricos y reales (según la simulación) son producidos porque el tiempo de simulación evidentemente no es infinito. Conforme se aumenta el tiempo de simulación, los errores teóricos y reales (según la simulación) tienden a converger al mismo valor.
 $G\left ( s \right )=\frac {1}{s^3+16s^2+80s}$
$G\left ( s \right )=\frac {1}{s^3+16s^2+80s}$
En primer lugar debemos obtener la ecución característica del sistema para compararla con la ecuación $1 + K P\left ( s \right ) = 0$:
$E.C. \equiv 1 + K G\left ( s \right ) = 0 \Rightarrow P\left ( s \right ) = G\left ( s \right ) = \frac {1}{s(s^2+16s+80)}$
Resolviendo los polos y ceros de P(s), tenemos:
$\left . \begin{array}{l} p_{1} = 0 \\ p_{2,3} = -8 \pm 4j\end{array}\right \} \Rightarrow n = 3, m = 0.$ No hay ceros finitos, así que habrá 3 ramas y todas fugarán a infinito.
El lugar de las raíces en el eje real coincide con $\left ( - \infty, 0 \right ]$
El número de asíntotas será: $na = 0,\ldots,n-m-1=0,\ldots,3-0-1=0,1,2$
$\left . \begin{array}{l} \theta_0 = \frac {180+0 \cdot 360}{3-0} = 60^\circ \\ \theta_1 = \frac {180+1 \cdot 360}{3-0} = 180^\circ \\ \theta_2 = \frac {180+2 \cdot 360}{3-0} = 300^\circ = -60^\circ \quad \end{array} \right \}$ El punto de corte de las asíntotas con el eje real es:$\sigma_c = \frac {0 - 8 + 4j - 8 - 4j}{3} = -5.33$
Para calcular los puntos de ruptura debemos resolver la ecuación:
$\frac {dP\left ( s \right )}{ds} = 0 = \frac {d}{ds} \left ( \frac {1} {s^3+16s^2+80s} \right ) = \frac {-(3s^2+32s+80) \cdot 1+0 \cdot (s^3+16s^2+80s)}{den^2} = 0$
$3s^2+32s+80 = 0 \Leftrightarrow s = -6.67; s= -4 $
Como ambas soluciones son reales, existirán 2 puntos de ruptura en los puntos calculados.
Para estudiar los cortes con el eje imaginario y la estabilidad del sistema, aplicaremos el test de Routh, pero en primer lugar debemos obtener la ecuación característica del sistema:
$E.C. \equiv 1+KP\left ( s \right ) = 0 \Rightarrow 1+K \frac {1}{s^3+16s^2+80s} = \frac {s^3+16s^2+80s+K}{s^3+16s^2+80s} = 0 \Rightarrow E.C. \equiv s^3+16s^2+80s+K = 0$
| s3 | 1 | 80 |
| s2 | 16 | K |
| s1 | b0 | |
| s0 | b1 |
$b_0 = -\frac {1}{16} \begin{vmatrix} 1 & 80 \\ 16 & K\end{vmatrix} = -\frac {1}{16} (K-1280) = 80 - \frac {K}{16}$
$b_1 = -\frac {1}{b_0} \begin{vmatrix} 16 & K \\ b_0 & 0\end{vmatrix} = -\frac {1}{b_0} (-b_0 K) = K$
Para que el sistema sea asintóticamente estable no debe haber cambios de signo en la 1ª columna de array de Routh, así que los valores límites son $b_0 = 0 \Rightarrow K = 1280$ y $b_1 = 0 \Rightarrow K = 0$.
Para saber qué sucede en los púntos límite resolveremos las ecuaciones auxiliares:
Si $b_0 = 0 \Rightarrow \mbox{ec. aux. } \equiv 16s^2+K = 0 \Rightarrow s = \pm \sqrt {-80} = \pm j8.94$. Es decir, si K=1280, tenemos dos polos complejos puros.
Si $b_1 = 0 \Rightarrow \mbox{ec. aux. } \equiv b_0s = 0 \Rightarrow s = 0$. Es decir, si K=0, tenemos un polo en el origen.
Concluyendo:
Si K = 0 o si K = 1280, el sistema será Marginalmente Estable.
Si 1280 > K > 0, todos los valores de la 1ª columna son positivos, luego el sistema será Asintóticamente Estable.
Si K > 1280, b0 será negativo, por lo que habrá 2 cambios de signo (2 polos con parte real positiva) y el sistema será Inestable.
Una vez que hemos realizado todos los cálculos, podemos trazar el lugar geométrico de las raíces. Éste empezará en los polos de lazo abierto de P(s) y terminará fugando a infinito por las 3 asíntatas que hemos obtenido. Además, debe tener los dos puntos de ruptura y los cortes con el eje imaginario calculados. Ten en cuenta que para que los polos de lazo cerrado lleguen al punto de ruptura calculado en -4 una rama debe llegar por la izquierda, así que obligatoriamente, los dos polos que en lazo abierto son complejos ya deben haber pasado a ser reales (ya han debido atravesar el punto de ruptura calculado en -6.67).
La única forma de dibujar el LGR cumpliendo los cálculos, y manteniendo la simetría con respecto al eje real, es la mostrada en la figura:

La figura la he generado con MATLAB mediante el siguiente comando: P=tf(1,[1 16 80 0]);rlocus(P)
Análisis: Si K = 0, el sistema será marginalmente estable. Al ir aumentando K, habrá un polo real negativo cercano al origen, y dos polos complejos conjugados cercanos al -8 de parte real; es decir, el polo del origen será dominante con respecto a los otros dos. Por lo tanto, en este punto el sistema en lazo cerrado se coportará como un sistema de primer orden, con un tiempo de asentamiento alto.
Si seguimos aumentando K, el polo real se va alejando del origen, reduciendo el tiempo de asentamiento del sistema. Si K sigue aumentando, los polos complejos llegarán al punto de ruptura situado en -6.67, por lo que tendremos 3 raices reales negativas, con 2 de ellas iguales. En este instante no se puede asegurar que el polo más a la derecha sea dominante sobre los otros dos, sin embargo, como todas las raices son reales negativas, sí sabemos que la respuesta del sistema será la suma de exponenciales, y por tanto tendrá una respuesta exenta de sobreimpulso.
Si K aumenta más, las raíces que estaban sobre el punto de ruptura en -6.67 se separan entre sí, alejándose una hacia $-\infty$ y acercándose la otra al punto de ruptura en -4. La raiz que en lazo abierto estaba en el origen sigue acercándose al punto de ruptura que está en -4, con lo que el tiempo de asentamiento del sistema seguirá disminuyendo.
La raiz que se aleja hacia $-\infty$ deja de ser representativa, ya que las otras dos se vuelven dominantes sobre ésta, de forma que la respuesta del sistema será similar a la de un sistema de 2º orden sobreamortiguado.
Si K sigue aumentando tendremos la misma situación, donde el tiempo de asentamiento segurá dismunuyendo y no habrá sobreimpulso, hasta que las 2 raíces dominantes en este instante coincidan en -4. En este instante tendremos un sistema similar a uno de 2º orden críticamente amortiguado.
Al amentar K, las 2 raíces dominantes pasarán a ser complejas conjugadas, por lo que tendremos una respuesta similar a la de un sistema de 2º orden subamortiguado. Inicialmente el sobreimpulso será pequeño, y el tiempo de asentamiento será aproximadamente algo superior a 1 segundo, pero al ir aumentando K, los polos van acercandose al eje imaginario y aumenta el ángulo que forman con respecto al origen; por lo tanto, en esta situación, tanto el tiempo de asentamiento como el sobreimpulso irán aumentando hasta el punto límite donde las raíces dominantes sean complejas puras ($\pm j8.94$), es este instante (K=1280) el sistema oscilará (será marginalmente estable).
Si a partir de este instante aumenta el valor de K, el sistema será inestable y su respuesta será una oscilación cuya amplitud aumenta infinitamente.
Nota. Puedes comprobar este análisis mediante el comando de MATLAB: P=tf(1,[1 16 80 0]);rltool(P)
Activa la simulación frente a una entrada escalón en 'Analysis/Response to Step Command' y elimina de la gráfica la señal de control (botón derecho sobre la gráfiva/Systems/Closed loop r to u). Variando las raices de lazo cerrado (cuadrado rosa) verás cómo evoluciona la respuesta dinámica del sistema.
Demuestre que los siguientes modelos de estado pertenecen al mismo sistema:
|
$\bf{\dot x} = \begin{pmatrix} -1 & 0 \\ 1 & -2 \end{pmatrix}\bf{x}+ \begin{pmatrix} 1 \\ 1 \end{pmatrix} u$ $y = \begin{pmatrix} 0 & 1 \end{pmatrix}\bf{x}$ |
$\bf{\dot x} = \begin{pmatrix} -3 & -2 \\ 1 & 0 \end{pmatrix}\bf{x}+ \begin{pmatrix} 2 \\ 0 \end{pmatrix} u$ $y = \begin{pmatrix} 0.5 & 1 \end{pmatrix}\bf{x}$ |
Para comprobar que los dos modelos de estado pertenecen al mismo sistema, es suficiente con obtener la función de transferencia de ambos modelos. Si efectivamente pertenecen al mismo sistema, sus funciones de transferencia han de ser idénticas.
$\bf{\dot x}=\bf{Ax}+\bf{B}u$
$y=\bf{Cx}+\bf{D}u$
$\textit{L} \Rightarrow s\bf{X}\left ( s \right ) = \bf{AX}\left ( s \right ) + \bf{B}U\left ( s \right ) \rightarrow s\bf{X}\left ( s \right ) - \bf{AX}\left ( s \right ) = \bf{B}U\left ( s \right )$
$\left( s\bf{I}-\bf{A}\right)\bf{X}\left ( s \right ) = \bf{B}U\left ( s \right ) \rightarrow \bf{X}\left ( s \right ) = \left( s\bf{I}-\bf{A}\right)^{-1}\bf{B}U\left ( s \right )$
$y = \bf{CX}\left ( s \right )+\bf{D}U\left ( s \right ) \rightarrow y=\bf{C}\left( s\bf{I}-\bf{A}\right)^{-1}\bf{B}U\left ( s \right ) + \bf{D}U\left ( s \right )$
Primer Modelo:
$\bf{A} = \begin{pmatrix} -1 & 0 \\ 1 & -2 \end{pmatrix}; \quad \bf{B} = \begin{pmatrix} 1 \\ 1 \end{pmatrix}; \quad \bf{C} = \begin{pmatrix} 0 & 1 \end{pmatrix}; \quad \bf{D} = 0$
$\left( s\bf{I}-\bf{A}\right) = \begin{pmatrix} s & 0 \\ 0 & s \end{pmatrix} - \begin{pmatrix} -1 & 0 \\ 1 & -2 \end{pmatrix} = \begin{pmatrix} s+1 & 0 \\ -1 & s+2 \end{pmatrix}$
$\mbox{Adjunta}\left( \left( s\bf{I}-\bf{A}\right) \right) = \begin{pmatrix} s+2 & 1 \\ 0 & s+1 \end{pmatrix} \rightarrow \mbox{Adjunta}\left( \left( s\bf{I}-\bf{A}\right) \right)^{\mbox{T}} = \begin{pmatrix} s+2 & 0 \\ 1 & s+1 \end{pmatrix}$
$\left| s\bf{I}-\bf{A}\right| = \begin{vmatrix} s+1 & 0 \\ -1 & s+2 \end{vmatrix} = (s+1)(s+2)=s^2+3s+2$
$\left( s\bf{I}-\bf{A}\right)^{-1} = \frac{\mbox{Adjunta}\left( \left( s\bf{I}-\bf{A}\right) \right)^{\mbox{T}}}{\left| s\bf{I}-\bf{A}\right|} = \frac {\begin{pmatrix} s+2 & 0 \\ 1 & s+1 \end{pmatrix}}{s^2+3s+2}$
$G\left ( s \right ) = \frac {Y\left ( s \right )}{U\left ( s \right )} = \begin{pmatrix} 0 & 1 \end{pmatrix} \frac {\begin{pmatrix} s+2 & 0 \\ 1 & s+1 \end{pmatrix}}{s^2+3s+2} \begin{pmatrix} 1 \\ 1 \end{pmatrix} + 0 = \frac {\begin{pmatrix} 1 & s+1 \end{pmatrix}}{s^2+3s+2} \begin{pmatrix} 1 \\ 1 \end{pmatrix} = \frac {1+s+1}{s^2+3s+2}$
$G\left ( s \right ) = \frac {s+2}{s^2+3s+2}$
Segundo Modelo:
$\bf{A} = \begin{pmatrix} -3 & -2 \\ 1 & 0 \end{pmatrix}; \quad \bf{B} = \begin{pmatrix} 2 \\ 0 \end{pmatrix}; \quad \bf{C} = \begin{pmatrix} 0.5 & 1 \end{pmatrix}; \quad \bf{D} = 0$
$\left( s\bf{I}-\bf{A}\right) = \begin{pmatrix} s & 0 \\ 0 & s \end{pmatrix} - \begin{pmatrix} -3 & -2 \\ 1 & 0 \end{pmatrix} = \begin{pmatrix} s+3 & 2 \\ -1 & s \end{pmatrix}$
$\mbox{Adjunta}\left( \left( s\bf{I}-\bf{A}\right) \right) = \begin{pmatrix} s & 1 \\ -2 & s+3 \end{pmatrix} \rightarrow \mbox{Adjunta}\left( \left( s\bf{I}-\bf{A}\right) \right)^{\mbox{T}} = \begin{pmatrix} s & -2 \\ 1 & s+3 \end{pmatrix}$
$\left| s\bf{I}-\bf{A}\right| = \begin{vmatrix} s+3 & 2 \\ -1 & s \end{vmatrix} = s(s+3)-(-2)=s^2+3s+2$
$\left( s\bf{I}-\bf{A}\right)^{-1} = \frac{\mbox{Adjunta}\left( \left( s\bf{I}-\bf{A}\right) \right)^{\mbox{T}}}{\left| s\bf{I}-\bf{A}\right|} = \frac {\begin{pmatrix} s & -2 \\ 1 & s+3 \end{pmatrix}}{s^2+3s+2}$
$G\left ( s \right ) = \frac {Y\left ( s \right )}{U\left ( s \right )} = \begin{pmatrix} 0.5 & 1 \end{pmatrix} \frac {\begin{pmatrix} s & -2 \\ 1 & s+3 \end{pmatrix}}{s^2+3s+2} \begin{pmatrix} 2 \\ 0 \end{pmatrix} + 0 = \frac {\begin{pmatrix} 0.5s+1 & s+2 \end{pmatrix}}{s^2+3s+2} \begin{pmatrix} 2 \\ 0 \end{pmatrix} = \frac {2(0.5s+1)}{s^2+3s+2}$
$G\left ( s \right ) = \frac {s+2}{s^2+3s+2}$
Conclusiones:
Puesto que las funciones de transferencia de ambos modelos son idénticas, queda demostrado que los dos modelos de estado pertenecen al mismo sistema.
Nota:
Ambas funciones de transferencia pueden simplificarse a $G\left ( s \right ) = 1/(s+1)$, esto quiere decir que los modelos de estado del ejercicio no son representaciones mínimas del sistema, ya que bastaría con una única variable de estado para modelarlo.
En la figura se muestra el vehículo explorador de Marte Spirit, el cual se puede controlar desde la Tierra mediante órdenes de trayectorias. Considerando que el diagrama de bloques simplificado del sistema es el que se muestra en la figura, se desea diseñar el sistema de control de velocidad del vehículo de forma que responda adecuadamente a los siguientes criterios de diseño:


$G\left ( s \right )=\dfrac{1}{s(s+1)(s+3)}$ $H\left ( s \right )=K_1s$
$C_1\left ( s \right ) = \dfrac {K_2}{s}$
$C_2\left ( s \right ) = K_2$
Recuerde: $x(\infty) = \lim_{s \to 0}sX\left ( s \right )$
a) En primer lugar debemos simplificar la realimentación interna formada por las funciones de transferencia G(s) y H(s). Si llamamos a la función de transferencia resultante G2(s), tenemos el siguiente diagrama de bloques reducido:
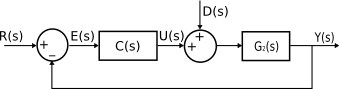
con $G_2\left ( s \right )=\dfrac {G\left ( s \right )}{1+G\left ( s \right )H\left ( s \right )} = \dfrac {\dfrac {1}{s(s+1)(s+3)}}{1+\dfrac {1}{s(s+1)(s+3)} K_1s} = \dfrac {1}{s(s+1)(s+3)+K_1s} = \dfrac {1}{s(s^2+4s+3+K_1)}$
Como puede observarse, G2(s) posee un polo en s=0, es decir, si C(s) no modifica el número de tipo del sistema, será de tipo 1. Para cumplir las especificaciones de error del ejercicio nos basta con que el sistema sea de tipo 1, ya que de esta forma tendrá error nulo para una entrada escalón y constante para una entrada de tipo rampa.
Como G2(s) ya tiene el número de tipo necesario, escogeremos el controlador dado por C2(s)=K2. Si se amenta el número de tipo de forma innecesaria se complica la estabilización del sistema. Es este caso concreto, si se escogiese C1(s) se puede comprobar fácilmente mediante el criterio de Routh que resulta imposible estabilizar el sistema, ya que debería cumplirse K2 > 0 y K2 < -(K1+4)/4, es decir, K2 positivo y negativo a la vez. (Házlo como ejercicio)
b) Para aplicar el test de estabilidad de Routh lo primero que necesitamos es la función de transferencia del sistema en lazo cerrado:
$\dfrac {Y\left ( s \right )}{R\left ( s \right )} = \dfrac {C\left ( s \right )G_2\left ( s \right )}{1+C\left ( s \right )G_2\left ( s \right )}$, así que la ecuación característica es $1+C\left ( s \right )G_2\left ( s \right ) = 0$, esto es:
$1+K_2 \dfrac {1}{s(s^2+4s+3+K_1)} = s(s^2+4s+3+K_1)+K_2 \Rightarrow s^3+4s^3+(3+K_1)s+K_2 = 0$.
| s3 | 1 | 3+K1 |
| s2 | 4 | K2 |
| s1 | b | |
| s0 | c |
$b = -\dfrac {1}{4} \begin{vmatrix}1 & 3+K_1 \\ 4 K_2\end{vmatrix} = -\dfrac {1}{4} (K_2-4(3+K_1))$
$c = -\dfrac {1}{b} \begin{vmatrix}4 & K_2 \\ b 0\end{vmatrix} = K_2$
Para que el sistema sea asintóticamene estable no debe haber ningún cambio de signo en la 1ª columna del array de Routh, es decir, debe cumplirse b>0 y c>0. Por lo tanto:
$b>0 \Rightarrow (3+K_1)-K_2/4 > 0 \Rightarrow 3+K_1 > K_2/4 \Rightarrow K_2 < 4(3+K_1)$
$c>0 \Rightarrow K_2 >0$
c) Cumpliendo las condiciones que hemos obtenido en el apartado anterior aseguramos la estabilidad asintótica del sistema en lazo cerrado, sin embargo, también hay que garantizar el cumplimiento de los errores de estado estacionario y limitar el efecto de las perturbaciones sobre la salida.
El error de estado estacionario de posición (velocidad del vehículo), es cero por el echo de que el sistema es te tipo 1 (tiene un polo en s=0 en lazo abierto).
El error de estado estacionario de velocidad (aceleración del vehículo), es:
$e_{ss}=\lim_{s \to 0}sE\left ( s \right )$
$\left . \begin{array}{l}E\left ( s \right )=R\left ( s \right )-Y\left ( s \right ) \\ Y\left ( s \right )=E\left ( s \right )C\left ( s \right )G_2\left ( s \right )\end{array}\right \} \Rightarrow E\left ( s \right ) = \dfrac {R\left ( s \right )}{1+C\left ( s \right )G_2\left ( s \right )}$
Como $e_{ss_{vel}} < 0.5 \Rightarrow \dfrac {3+K_1}{K_2}<0.5 \Rightarrow K_2 > 2(3+K_1)$
Para calcular el efecto de una perturbación sobre la salida debemos obtener la función de transferencia $\dfrac {Y\left ( s \right )}{D\left ( s \right )}$. Si se hace R(s)=0 y se observa el diagrama de bloques resultante, es fácil deducir que:
$\dfrac {Y\left ( s \right )}{D\left ( s \right )} = D\left ( s \right )\dfrac {G_2\left ( s \right )}{1+C\left ( s \right )G_2\left ( s \right )} = \dfrac {1}{s(s^2+4s+3+K_1)+K_2}$
Por lo tanto, siendo D(s) una entrada escalón:
$y(\infty) = \lim_{s \to 0}sY\left ( s \right ) = \lim_{s \to 0} s \dfrac {\dfrac {1}{s}}{s(s^2+4s+3+K_1)+K_2} = \dfrac 1 {K_2} < 0.1 \Rightarrow K_2 >10$
d) Resumiendo, para que el sistema sea asintóticamente estable y se satisfagan los requerimientos del diseño, debe cumplirse:
$\left . \begin{array}{l}1 < K_1 < 3 \\ K_2 < 4(3+K_1) \\ K_2 > 0 \\ K_2 > 2(3+K_1) \\ K_2 > 10\end{array}\right \} \Rightarrow$ Por lo que si se escoge $K_1 =2 \Rightarrow 10 < K_2 < 20$. Por ejemplo, $K_2 = 15$.
e y f) El código que genera todas las simulaciones es:
clc,clear all,close all
% Definición del problema
G=zpk([],[0,-1,-3],1);
K1=2;
H=zpk(0,[],K1);
G2=feedback(G,H);
% Diseño
fprintf('Límites para K2: K2 > %d y K2 < %d\n',max(10,2*(3+K1)),4*(3+K1))
K2=(4*(3+K1)-max(10,2*(3+K1)))/2+max(10,2*(3+K1));
fprintf('Si se escoge K2 en el centro del rango => K2 = %d\n\n',K2)
C=K2;
Glc=feedback(C*G2,1);
% Simulación frente a una entrada escalón
[y1,t]=step(Glc);
plot(t,ones(size(t)),'r--',t,y1)
title('Respuesta a entrada escalón')
xlabel('tiempo (s)'), ylabel('velocidad (m/s)')
error_posicion_teorico=0;
error_posicion_real=1-y1(end);
fprintf('Error de posición:\n\tTeórico: %d\n\tReal: %d\n\n',error_posicion_teorico,error_posicion_real)
% Simulación frente a una entrada rampa
figure
[y2,t]=step(Glc*tf(1,[1,0]),t);
plot(t,t,'r--',t,y2)
title('Respuesta a entrada rampa')
xlabel('tiempo (s)'), ylabel('aceleración (m/s^2)')
error_velocidad_teorico=(3+K1)/K2;
error_velocidad_real=t(end)-y2(end);
fprintf('Error de velocidad:\n\tTeórico: %d\n\tReal: %d\n\n',error_velocidad_teorico,error_velocidad_real)
% Simulación del efecto de la perturbación
figure
Gper=feedback(G2,C);
[y3,t]=step(Gper,t);
plot(t,ones(size(t)),'r--',t,y3)
title('Respuesta a una perturbación escalón')
xlabel('tiempo (s)'), ylabel('velocidad (m/s)')
perturbacion_teorico=1/K2;
perturbacion_real=y3(end);
fprintf('Efecto de una perturbación escalón:\n\tTeórico: %d\n\tReal: %d\n\n',perturbacion_teorico,perturbacion_real)
Los resultados de la consola de MATLAB son:
Límites para K2: K2 > 10 y K2 < 20
Si se escoge K2 en el centro del rango => K2 = 15
Error de posición:
Teórico: 0
Real: 6.026208e-03
Error de velocidad:
Teórico: 3.333333e-01
Real: 3.333037e-01
Efecto de una perturbación escalón:
Teórico: 6.666667e-02
Real: 6.626492e-02
Y las figuras resultantes:
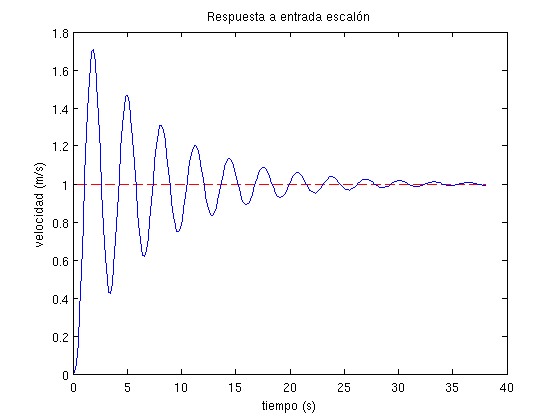
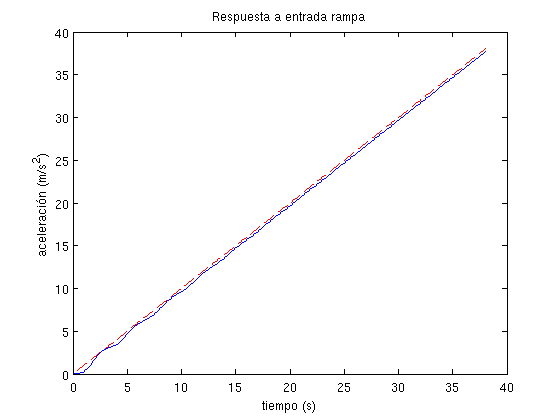
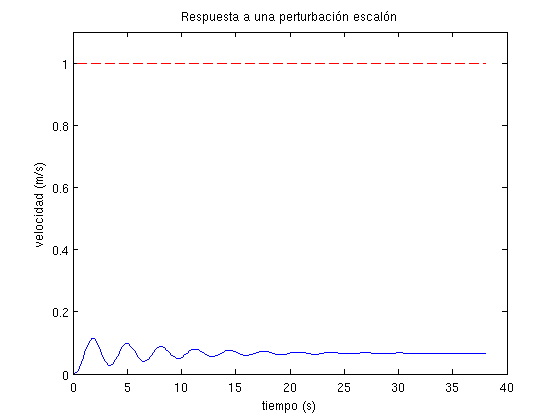
Como puede observarse, tanto en los resultados de la consola como en las representaciones gráficas, se cumplen las condiciones del diseño. Las pequeñas diferencias existentes entre los errores teóricos y reales (según la simulación) son producidos porque el tiempo de simulación evidentemente no es infinito. Conforme se aumenta el tiempo de simulación, los errores teóricos y reales (según la simulación) tienden a converger al mismo valor.
La respuesta dinámica del sistema resultante no es muy buena, ya que presenta muchísima oscilación y un tiempo de asentamiento excesivo. Sería posible escoger un valor más adecuado haciendo un análisis más detallado del sistema. Para ello podemos representar el lugar geométrico de las raíces para el parámetro K2, escogiendo previamente un valor de K1. Si se escoge K1 = 1 y K2 = 10, mejora el tiempo de asentamiento que se sitúa en 12 segundos, y el sobreimpulso, que pasa a ser del 49%, manteniéndose el cumplimiento de los requisitos del problema. Aún así la respuesta del sistema no es del todo satisfactoria. Para obtener una mejor respuesta dinámica sería necesario diseñar un controlador distinto a los propuestos, pero esto forma parte del temario de Automátcia II (es un buen ejercicio si estáis cursado esta asignatura).
Dada la siguiente ecuación diferencial:
$$\dfrac{\partial^3 y(t)}{\partial t^3}+4\dfrac{\partial^2 y(t)}{\partial t^2}+5\dfrac{\partial y(t)}{\partial t}+y(t)+\sin(y(t))-r(t)=0$$
1) Obtener un modelo de estado que represente el sistema no lineal.
2) Obtener un modelo de estado lineal del sistema suponiendo que éste opera en las cercanías del punto y(t)=0
3) Simular durante 20 segundos tanto el sistema lineal como el sistema no lineal, si se toma como punto inicial el origen, para r(t)=1 y r(t)=5, comentando los resultados de la simulación.
Deberá crear una función en un archivo M que describa el sistema no lineal, para poder simularlo mediante la instrucción ode 45
APARTADO 1.
Como la mayor derivada es 3, sabemos que N=3.
\[
\begin{array}{l}
x1 = y(t) \\
\mathop {x1}\limits^ \bullet = \mathop y\limits^ \bullet (t) = x2 \\
\mathop x\limits^ \bullet 2 = \mathop y\limits^{ \bullet \bullet } (t) = x3 \\
\mathop x\limits^ \bullet 3 = \\
\end{array}
\]
Despejamos de la ecuación \[\mathop x\limits^ \bullet 3\] pero primero reemplazamos los nombres
\[
\begin{array}{l}
\mathop x\limits^ \bullet 3 + 4x3 + 5x2 + x1 + sen(x1) - r(t) = 0 \\
\mathop x\limits^ \bullet 3 = - 4x3 - 5x2 - x1 - sen(x1) + r(t) \\
\end{array}
\]
Por tanto el modelo de estado seria:
\[
\begin{array}{l}
\mathop {x1}\limits^ \bullet = x2 \\
\mathop x\limits^ \bullet 2 = x3 \\
\mathop x\limits^ \bullet 3 = - 4x3 - 5x2 - x1 - sen(x1) + r(t) \\
\end{array}
\]
Y la sálida será:
\[
y(t) = x1
\]
APARTADO 2.
\[
\frac{{\partial ^3 y(t)}}{{\partial t^3 }} + 4\frac{{\partial ^2 y(t)}}{{\partial t^2 }} + 5\frac{{\partial y(t)}}{{\partial t}} + y(t) + sen(y(t)) - r(t) = 0
\]
Como \[
sen(y(t))
\]
es no lineal, lo linealizamos por medio del polinomio de Taylor.
\[
\begin{array}{l}
sen(y(t)) \cong sen(y_0 (t)) + \left. {\frac{{\partial sen(y(t))}}{{\partial t}}} \right|_{x_0 } *\frac{{(y - y_0 )}}{1} + ... \\
sen(y(t)) \cong sen(y_0 (t)) + \cos y(t)*(y - y_0 ) + ... \\
\end{array}
\]
Estudiamos el caso para \[
y_0 (t) = 0
\]
Que reemplazandolo será
\[
\begin{array}{l}
sen(y(t)) \cong 0 + 1(y - 0) \\
sen(y(t)) \cong y \\
\end{array}
\]
Por tanto la ecuación quedaría
\[
\begin{array}{l}
\frac{{\partial ^3 y(t)}}{{\partial t^3 }} + 4\frac{{\partial ^2 y(t)}}{{\partial t^2 }} + 5\frac{{\partial y(t)}}{{\partial t}} + y(t) + y(t) - r(t) = 0 \\
\frac{{\partial ^3 y(t)}}{{\partial t^3 }} + 4\frac{{\partial ^2 y(t)}}{{\partial t^2 }} + 5\frac{{\partial y(t)}}{{\partial t}} + 2y(t) - r(t) = 0 \\
\end{array}
\]
Ahora convertimos la ecuación en modelo de estados
Como la mayor derivada es 3, sabemos que N=3.
\[
\begin{array}{l}
x1 = y(t) \\
\mathop {x1}\limits^ \bullet = \mathop y\limits^ \bullet (t) = x2 \\
\mathop x\limits^ \bullet 2 = \mathop y\limits^{ \bullet \bullet } (t) = x3 \\
\end{array}
\]
Despejamos de la ecuación \[\mathop x\limits^ \bullet 3\] pero primero reemplazamos los nombres
\[
\begin{array}{l}
\mathop x\limits^ \bullet 3 + 4x3 + 5x2 + 2x1 - r(t) = 0 \\
\mathop x\limits^ \bullet 3 = - 4x3 - 5x2 - 2x1 + r(t) \\
\end{array}
\]
Por tanto el modelo de estado seria:
\[
\begin{array}{l}
\mathop {x1}\limits^ \bullet = x2 \\
\mathop x\limits^ \bullet 2 = x3 \\
\mathop x\limits^ \bullet 3 = - 4x3 - 5x2 - 2x1 + r(t) \\
\end{array}
\]
Y la sálida será:
\[
y(t) = x1
\]
Representado de forma matricial seria.
\[
\left[ {\begin{array}{*{20}c}
{\mathop {x1}\limits^ \bullet } \\
{\mathop {x2}\limits^ \bullet } \\
{\mathop {x3}\limits^ \bullet } \\
\end{array}} \right] = \left[ {\begin{array}{*{20}c}
0 & 1 & 0 \\
0 & 0 & 1 \\
{ - 2} & { - 5} & { - 4} \\
\end{array}} \right]*\left[ {\begin{array}{*{20}c}
{\mathop {x1}\limits^{} } \\
{\mathop {x2}\limits^{} } \\
{\mathop {x3}\limits^{} } \\
\end{array}} \right] + \left[ {\begin{array}{*{20}c}
0 \\
0 \\
1 \\
\end{array}} \right]*r(t)
\]
Y la sálida será:
\[
\left[ {y(t)} \right] = \left[ {\begin{array}{*{20}c}
1 & 0 & 0 \\
\end{array}} \right]*\left[ {\begin{array}{*{20}c}
{x1} \\
{x2} \\
{x3} \\
\end{array}} \right] + \left[ 0 \right]*r(t)
\]
APARTADO 3.
Primero lo haremos para el sistema no lineal.
function dx=nolineal(t,x)
R=1; Como nos dice, que simularlo con R=1 y R=5, aqui en la otra simulación simplemente lo cambiamos por 5
dx=zeros(3,1);
dx(1)=x(2);
dx(2)=x(3);
dx(3)=-x(1)-5*x(2)-4*x(3)+R-sin(x(1));
Nota: Al guardar la función, ponerle el mismo nombre que le hemos puesto a la función, en este caso "nolineal"
x0=[0;0;0];
tf=20;
[t,x]=ode45(@nolineal,[0,tf],x0);
plot(t,x),grid
xlabel('tiempos');
ylabel('variables de estado')
legend ('x_1','x_2','x_3')
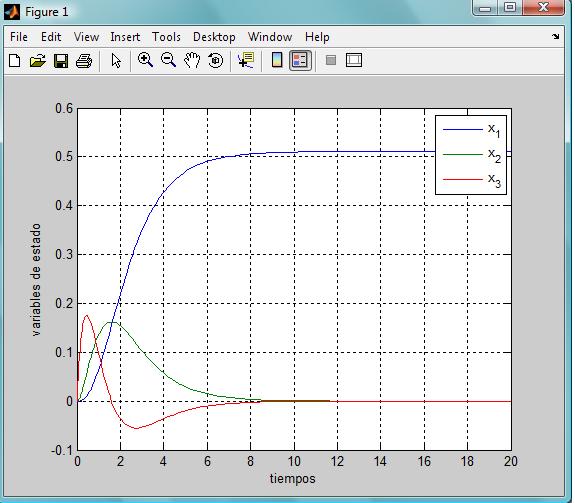
Y la gráfica que nos devuelve el sistema es
Ahora lo haremos para el sistema lineal
clc, clear all, close all
A=[0,1,0;0,0,1;-2,-5,-4];
B=[0;0;1];
C=[1,0,0];
D=[0];
Sistema1=ss(A,B,C,D); %Coje las 4 matrices y lo convierte en un sistema lineal
step(Sistema1,20)
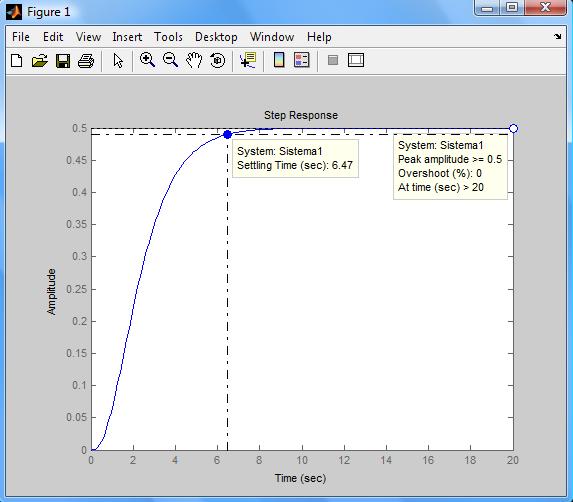
Y la gráfica que nos devuelve el sistema es
Ejercicio 2) (4 Puntos). Dado el sistema de control de la figura 1, donde
$G(s) = \dfrac{{(s + 0.5)}}{{(s + 0.1)(3s + 1)}},$ $C(s)=K$ y $H(s) = \dfrac{1}{{(0.4s + 1)}}$
a) Dibuje la región del plano S donde deberán situarse las raíces dominantes para que el sistema
posea un sobreimpulso máximo del 10% y un tiempo de asentamiento menor de 8 segundos.
b) Calcule la condición que debe satisfacer el controlador para que el error de estado estacionario
de posición sea inferior al 6%.
c) Escoja un valor de K para que se cumplan las especificaciones del diseño dadas en los
apartados anteriores. Explique detalladamente el proceso de diseño seguido.
d) Simule el comportamiento del sistema y comente los resultados de la simulación.
e) ¿Qué sucedería si el requisito de error de posición fuese inferior al 1%? ¿Qué solución
adoptaría? Apoye su argumentación mediante los cálculos y simulaciones que considere
necesarios.
a)El plano S para un sobreimpulso máximo del 10% y un tiempo de asentamiento menor de 8 segundos, es el resultante.
\[ M_p < 10\% = 0.1\]
\[M_p = e^{\dfrac{{ - \delta \pi }}{{\sqrt {1 - \delta ^2 } }}} \]
\[\delta = \sqrt {\dfrac{{(LnM_p )^2 }}{{\pi ^2 + (LnM_p )^2 }}} \Rightarrow \delta \geq 0.5911\]
\[t_s < 8s.\]
\[ \cos \beta = \delta\]
\[\beta \leq arcos (0.5911) \rightarrow \beta \leq 53.73º\]
\[
t_s \approx \dfrac{4}
{{\delta w_n }} < 8s \rightarrow{{}} \delta w_n > \dfrac{4}{8}, \delta w_n > 0.5
\]
Para que se cumpla las especificaciones de sobreimpulso y tiempo de asentamiento dado los polos deben de estar dentro del plano S dibujado.
b) Para un error de posición inferior al 6% la k será la siguiente.
E(s)= R(s)-B(s)
B(s)= H(s)* Y(s)
Y(s)= E(s)*C(s)*G(s)
\[
E(s) = R(s)\dfrac{1}
{{1 + H(s)*C(s)*G(s)}}
\]
\[
E(s) = R(s)\dfrac{{(0.4s + 1)(3s + 1)(s + 0.1)}}
{{(0.4s + 1)(3s + 1)(s + 0.1) + k(s + 0.5)}}
\]
\[
x(\infty ) = \mathop {Lim}\limits_{s \to 0} s\dfrac{1}
{s}\dfrac{{(0.4s + 1)(3s + 1)(s + 0.1)}}
{{(0.4s + 1)(3s + 1)(s + 0.1) + k(s + 0.5)}}
\]
\[
\dfrac{{0.1}}
{{0.1 + 0.5K}} < 0.06;K > 3,13
\]
Para que el error de posición del sistema sea inferior a 6% K debe de ser mayor a 3.13
c) Para que se cumpla las especificaciones la K debe de estar dentro del plano S descrito anteriormente y ser mayor de 3.13, por ello usare una K de 3.3
d) la simulación es la siguiente
clc,clear all, close all;
%K=3.2;
G=tf([1 0.5],[3 1.3 0.1])
H=tf([1],[0.4 1])
Gba=series(G,H);
rlocus(Gba)
sgrid
K=rlocfind(Gba)
figure
Gbc=feedback(K*G,H)
%veo respuesta sistema
step(Gbc)
%otra grafica para ver el error posicion
figure
[y,t]=step(Gbc);
plot(t,y)
hold on
X=ones(1,length(t));
plot(t,X,'k--')
hold off
error_posicion=(1-y(end))*100
En el grafico anterior se observa que como hemos seleccionado una ganancia K de 3.3 aproximadamente y que esta dentro del plano S dibujado anteriormente. Pero se observa que de algún modo solo cumplimos las especificaciones de error del 6% y el tiempo de asentamiento ya que es sobre impulso obtenido es del 11.9%, un 1.9% mas de lo deseado, en definitiva esta ganancia aproximadamente será la mas deseada por nosotros aunque asumamos ese 1.9% mas de sobre impulso. Ya que veremos que para un gran amplio margen de las ganancias, el tiempo de asentamiento se cumple, pero para el caso del sobreimpulso y del error de posición si uno mejor el otro empeora.
Para k>3.3
Se observa como que el error de posición disminuye a mayor ganancia de K, pero el sobre impulso aumenta cada vez mas cuanto mas no alejemos del eje real.
Para que el sobreimpulso sea menor del 10% tenemos que desplazarnos hacia la derecha en el eje real disminuyendo la ganancia
Para k<3.13
Para esta zona a la derecha de K=3.13 el sobreimpulso disminuye pero el error aumenta es de un 7.33% e ira aumentado cuanto menor sea la ganancia.
e) para un error de posición inferior al 1% quedara una restricción de k como la siguiente.
\[
x(\infty ) = \mathop {Lim}\limits_{s \to 0} s\dfrac{1}
{s}\dfrac{{(0.4s + 1)(3s + 1)(s + 0.1)}}
{{(0.4s + 1)(3s + 1)(s + 0.1) + k(s + 0.5)}}
\]
\[
\dfrac{{0.1}}
{{0.1 + 0.5K}} < 0.01;K > 19.8
\]
Para K=20
clc,clear all, close all;
%K=3.2;
G=tf([1 0.5],[3 1.3 0.1])
H=tf([1],[0.4 1])
Gba=series(G,H);
rlocus(Gba)
sgrid
K=rlocfind(Gba)
figure
Gbc=feedback(K*G,H)
%veo respuesta sistema
step(Gbc)
%otra grafica para ver el error posicion
figure
[y,t]=step(Gbc);
plot(t,y)
hold on
X=ones(1,length(t));
plot(t,X,'k--')
hold off
error_posicion=(1-y(end))*100
%con k=20
K=20
figure
Gbc=feedback(K*G,H)
%veo respuesta sistema
step(Gbc)
%otra grafica para ver el error posicion
figure
[y,t]=step(Gbc);
plot(t,y)
hold on
X=ones(1,length(t));
plot(t,X,'k--')
hold off
error_posicion=(1-y(end))*
Se puede observar que el sobreimpulso es muy elevado de un 93.3% el sistema hasta llegar a la posición deseada va estar oscilado mucho. Este sobreimpulso no es aconsejable asumir por algunas razones como el daño a la electrónica asociada o por el gasto energético elevado, aunque todo depende del sistema a controlar.
Se puede observar que el error al 1% si se cumple como muestra la siguiente grafica, ya que ilustra lo próximo a la entrada escalón, tan solo cometiendo un error del 0.95%.
Para una velocidad $v$ constante, la dinámica del submarino de la figura viene determinada por el siguiente conjunto de ecuaciones diferenciales:
 |
$$ \begin{array}{l} \theta (t) = -125 \dfrac{\text{d}^2\theta (t)}{\text{d}t^2} - 15\dfrac{\text{d}\theta (t)}{\text{d}t} + 17 \alpha (t) - 14 \delta (t)\\~\\ \dfrac{\text{d}\alpha (t)}{\text{d}t} = 0.07 \dfrac{\text{d}\theta (t)}{\text{d}t} + 0.075 \delta (t) - 0.3 \alpha (t)\\~\\ \dfrac{\text{d}h (t)}{\text{d}t} = 8 \theta (t) - 8 \alpha (t) \end{array}$$ |
donde $\theta (t)$ es el ángulo con respecto a la horizontal, $\alpha (t)$ es el ángulo de ataque del submarino, $h(t)$ es su profundidad y $\delta (t)$ es la inclinación de la superficie de control (alerón de popa):
Se solicita:
Recuerde, siendo T el periodo de muestreo y el tiempo discreto, la derivada puede aproximarse por:
$$\dfrac{\text{d}x(t)}{\text{d}t} \simeq \dfrac{x(k+1) - x(k)}{T}$$
Solución.
1. Modelo de estado:
Asignamos variables de estado de la siguiente manera:
X1=θ(t) --> dX1=d θ(t) X3=α(t) --> dX3=dα(t)
X2= d θ(t) --> dX2= d2 θ(t) X4= µ(t) --> dX4=dµ(t)
Creamos el modelo de estado despejando las derivadas y el modelo de salida.
Modelo de estado (lineal):
dX1= X2
dX2= -0.008X1 -0.12X2+0.136 X3-14δ(t);
dX3= 0.07X2 0.075δ(t) -0.3X3;
dX4= 8X1 -8X3;
Modelo de salida (lineal):
µ(t) = X4
Si un modelo es lineal, se puede poner de forma matricial en la forma xpunto = A*x + B*u. para el modelo de estado y
y=C*x + D*u . (Las matrices A,B,C y D las podemos ver en el codigo fuente de Matlab adjunto).
2. Discretizar para T=0.01.
Usamos la fórmula vista en clase: x(k+1) = (1 + TA)x(k) + BTu(k) donde (1 + TA) será la matiz A discretizada y BT la matriz B discretizada.
Matlab nos da el resultado :
Código fuente de Matlab:
clc, clear all, close all
A=[0 1 0 0; -0.008 -0.12 0.136 0; 0 0.07 -0.3 0; 8 0 -8 0];
B=[0;-14;0.075;0];
C=[0 0 0 1];
D=0;
T=0.01;
Ad=eye(4)+T*A;
Bd=T*B;
Modelod=ss(Ad,Bd,C,D,T);
[y,t,x]=step(Modelod); / Simulamos frente a una entrada escalón
plot(t,y); title('apdo 3)'),xlabel('Tiempo'), ylabel('Profundidad'); / representamos gráficamente la salida.
4. En la figura se aprecia que al cambiar la inclinación (entrada) 1º el submarino se va sumergiendo y se quedará así siempre o hasta chocar con el fondo suponiendo que lo haya, luego el sistema es inestable.
Wikiapunte realizado por:
David Romero Delgado Francisco Canelo Santos
Sancho Santiago Blanco Enrique Casimiro-Soriguer Serrano
El sistema de la figura está formado por dos depósitos interconectados donde $q_e(t)$ es el caudal entrante en cada depósito y, para cada uno de los depósitos, $h_1(t)$ y $h_2(t)$ es la altura de líquido, $q_1(t)$ y $q_2(t)$ el caudal de salida, y $A_1$ y $A_2$ el área transversal. La dinámica del sistema puede ser representada mediante el siguiente conjunto de ecuaciones:
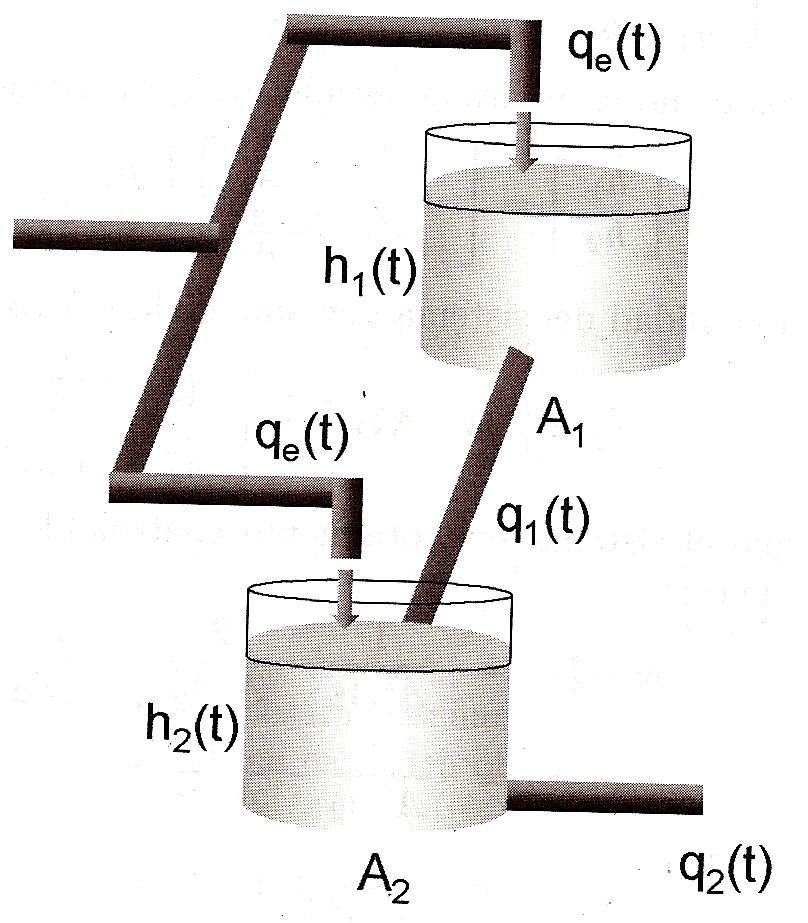 |
$A_1 \dot{h}_1(t)=q_e(t)-q_1(t)$ $A_1=2 m^2$ |
Se solicita:
| a) T = 0.1s | b) T = 0.3s | c) T = 0.8s |
Recuerde:
$\dfrac{\text{d}x(t)}{\text{d}t} \simeq \dfrac{x(k+1) - x(k)}{T}$, siendo T el periodo de muestreo y el tiempo discreto.
$t_s \approx 5 \tau$, siendo $t_s$ el tiempo de establecimiento y $\tau$ la constante de tiempo del sistema.
1.) Las variables de entrada del sistema, se aprecian claramente en el gráfico que muestra el sistema a analizar, determinando que la entrada al sistema es qe(t), debido a que son las únicas tuberías que pueden incorporar fluido a los depósitos A1 y A2. Del mismo modo, se determina que la variable de salida será q2(t), ya que es la única variable que sale del sistema al exterior (fuera de lo representado en el esquema).
En este caso, como podemos apreciar, los elementos capaces de almacenar fluido en el sistema serán los depósitos, siendo pues las variables el volumen que habrá que hay en ellos, es decir, h1(t) y h2(t), de modo que podemos modelar el sistema.
Antes de modelar, reducimos las ecuaciones del mismo, obteniendo 2 ecuaciones, debido a que el sistema nos presenta 2 elementos almacenadores de 1er orden.
${A_1}\cdot{{\dot h}_1}\left( t \right) = {q_e}\left( t \right) - {h_1}\left( t \right) + {h_2}\left( t \right)$
${A_2}\cdot{{\dot h}_2}\left( t \right) = {q_e}\left( t \right) + {h_1}\left( t \right) - 2{h_2}\left( t \right)$
Ahora, hacemos la siguiente operación:
${x_1} = {h_1}\left( t \right)\mathop \to \limits^{\frac{{dx}}{{dt}}} {{\dot X}_1} = \frac{{d{h_1}(t)}}{{dt}} = {{\dot h}_1}(t)$
${x_2} = {h_2}\left( t \right)\mathop \to \limits^{\frac{{dx}}{{dt}}} {{\dot X}_2} = \frac{{d{h_2}(t)}}{{dt}} = {{\dot h}_2}(t)$
El sistema quedará entonces del siguiente modo:
${{\dot X}_1}\left( t \right) = \frac{{ - {x_1}\left( t \right)}}{{{A_1}}} + \frac{{{x_2}\left( t \right)}}{{{A_1}}} + \frac{{{q_e}\left( t \right)}}{{{A_1}}}$
${{\dot X}_2}\left( t \right) = \frac{{{x_1}\left( t \right)}}{{{A_2}}} - \frac{{2{x_2}\left( t \right)}}{{{A_2}}} + \frac{{{q_e}\left( t \right)}}{{{A_2}}}$
Al ser un sistema lineal, se puede poner de forma matricial, siendo este el que usaremos para realizar las simulaciones pertinentes.
$\left[ {\begin{array}{*{20}{c}}
{{{\dot X}_1}}\\
{{{\dot X}_2}}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{-\frac{1}{{{A_1}}}}&{\frac{1}{{{A_1}}}}\\
{\frac{1}{{{A_2}}}}&{\frac{{ - 2}}{{{A_2}}}}
\end{array}} \right]\cdot\left[ {\begin{array}{*{20}{c}}
{{x_1}}\\
{{x_2}}
\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}
{\frac{1}{{{A_1}}}}\\
{\frac{1}{{{A_2}}}}
\end{array}} \right]\cdot{q_e}(t)$
La ecuación de salida, al ser q2(t)=h2(t), será:
$y = \left[ {\begin{array}{*{20}{c}}
0&1
\end{array}} \right]\cdot\left[ {\begin{array}{*{20}{c}}
{{x_1}}\\
{{x_2}}
\end{array}} \right] + 0\cdot{q_e}(t)$
2.) Para determinar correctamente el periodo del modelo discreto, simularemos el modelo no discreto en matlab, obteniendo así una función de la salida, en este caso, correspondiente a q2(t), para lo cual emplearemos el siguiente código de matlab:
clc, clear all, close all
%---------------------------------------------------------------------
%Simulación del sistema no discretizado:
%---------------------------------------------------------------------
%Constantes del sistema:
A1=2; %m^2
A2=1; %m^2
%Matrices del modelo:
A=[-1/A1, 1/A1; 1/A2, -2/A2];
B=[1/A1; 1/A2];
C=[0,1];
D=0;
%Declaración del modelo y simulación:
Sistema=ss(A,B,C,D);
[y,t,x]=step(Sistema);
figure
plot(t,y) %Salida del sistema
title('Modelo no discretizado'),xlabel('tiempo')
ylabel('caudal'),legend('y')
Simulando, obtenemos la siguiente gráfica, donde marcamos Tau, siendo su valor el valor que toma la gráfica cuando ha llegado al 63% de su valor total:
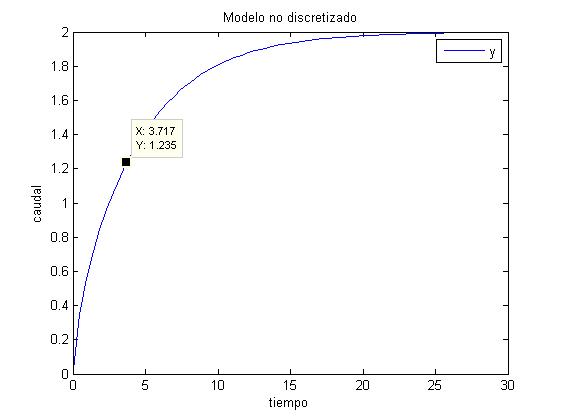
Como se aprecia en la gráfica anterior, el valor de Tau, es 3.717, de modo que aplicamos la siguiente fórmula para obtener el periodo:
$\frac{{10}}{{Tau}} \le \frac{1}{T} \le \frac{{20}}{{Tau}}$
Aplicando la ecuación, obtendremos que:
$\frac{{Tau}}{{10}} \le T \le \frac{{Tau}}{{20}}\mathop \Rightarrow \limits^{Tau = 3.717} 0.18585 \le T \le 0.3717$
Al tener que estar T comprendido entre esos dos valores, elegimos el único de los 3 dados por el problema que cumple la ecuación, de modo que T=0.3 (opción b) para todo lo que resta de problema.
3.) Antes de poner el modelo discretizado, habrá que obtener la forma de discretizar el sistema, para lo cual, utilizaremos la definición de derivada dada en el enunciado:
$\dfrac{\text{d}x(t)}{\text{d}t} \simeq \dfrac{x(k+1) - x(k)}{T}$
Aplicandola a un sistema general, para llegar a la solución particular de nuestro sistema, siendo:
$\frac{{\vec x\left( {k + 1} \right) - \vec x\left( k \right)}}{T} = A\cdot\vec x\left( k \right) + B\cdot\vec u\left( k \right)$
$\vec x(k + 1) - \vec x(k) = T\cdot A\cdot\vec x(k) + T\cdot B\cdot\vec u(k)$
$\vec x\left( {k + 1} \right) = [T\cdot A + I]\cdot\vec x\left( k \right) + T\cdot B\cdot\vec u\left( k \right)$
Nuestro sistema discretizado tendría la siguiente forma:
$\left[ {\begin{array}{*{20}{c}}
{{x_1}(k + 1)}\\
{{x_2}(k + 1)}
\end{array}} \right] = \left[ {T*\left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{\frac{{ - 1}}{{{A_1}}}}&{\frac{1}{{{A_1}}}}\\
{\frac{1}{{{A_2}}}}&{\frac{{ - 2}}{{{A_2}}}}
\end{array}}
\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}
1&0\\
0&1
\end{array}} \right]} \right]\cdot\left[ {\begin{array}{*{20}{c}}
{{x_1}}\\
{\begin{array}{*{20}{c}}
{{x_2}}
\end{array}}
\end{array}} \right] + T*\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{{A_1}}}}\\
{\frac{1}{{{A_2}}}}
\end{array}} \right]\cdot{q_e}\left( k \right)$
$\left[ {\begin{array}{*{20}{c}}
{{x_1}(k + 1)}\\
{{x_2}(k + 1)}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{\frac{{ - T}}{{{A_1}}} + 1}&{\frac{T}{{{A_1}}}}\\
{\frac{T}{{{A_2}}}}&{\frac{{ - 2T}}{{{A_2}}} + 1}
\end{array}}
\end{array}} \right]\cdot\left[ {\begin{array}{*{20}{c}}
{{x_1}}\\
{\begin{array}{*{20}{c}}
{{x_2}}
\end{array}}
\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}
{\frac{T}{{{A_1}}}}\\
{\frac{T}{{{A_2}}}}
\end{array}} \right]\cdot{q_e}\left( k \right)$
Quedando de forma numérica:
$\left[ {\begin{array}{*{20}{c}}
{{x_1}(k + 1)}\\
{{x_2}(k + 1)}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{0.85}&{0.15}\\
{0.3}&{0.4}
\end{array}}
\end{array}} \right]\cdot\left[ {\begin{array}{*{20}{c}}
{{x_1}}\\
{\begin{array}{*{20}{c}}
{{x_2}}
\end{array}}
\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}
{0.15}\\
{0.3}
\end{array}} \right]\cdot{q_e}\left( k \right)$
Del mismo obtenemos salida del sistema, siendo para este caso:
$y = \left[ {\begin{array}{*{20}{c}}
0&1
\end{array}} \right]\cdot\left[ {\begin{array}{*{20}{c}}
{{x_1}(k)}\\
{{x_2}(k)}
\end{array}} \right] + 0\cdot{q_e}(k)$
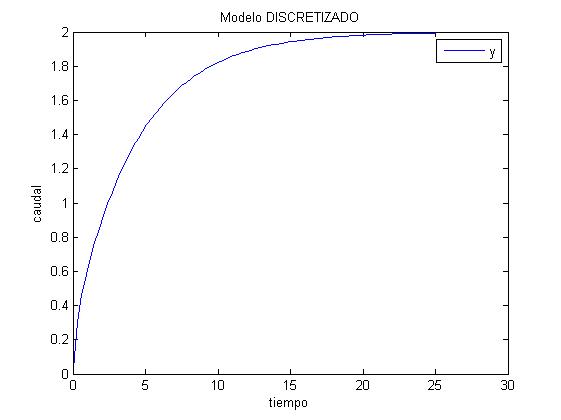
4.) Simularemos el sistema discretizado, siendo la salida a representar q2(t) discretizado, siendo el código de matlab el siguiente:
clc, clear all, close all
%Constantes del sistema:
A1=2; %m^2
A2=1; %m^2
%Matrices del modelo:
A=[-1/A1, 1/A1; 1/A2, -2/A2];
B=[1/A1; 1/A2];
C=[0,1];
D=0;
%Periodo (T)
T=0.3; %segundos
%Matrices del sistema
Ak=[T*A+eye(2,2)];
Bk=T*B;
Ck=C;
Dk=D;
%Simulación del sistema
Sistema_discreto=ss(Ak,Bk,Ck,Dk,T);
[yk,tk,xk]=step(Sistema_discreto);
figure
plot(tk,yk) %Salida del sistema
title('Modelo DISCRETIZADO'), xlabel('tiempo'),ylabel('caudal'),legend('y')
La gráfica obtenida es la siguiente:
5.) Cuando se le aplica un caudal de entrada, el sistema va llenando los depósitos hasta que la salida consigue un caudal estable.
Al ser un sistema que trabaja en una región lineal, podemos asegurar la estabilidad hallando los autovalores de la matriz de estados del sistema (matriz A), lo cual se realiza en matlab gracias al siguiente código, el cual, irá al final del código anterior:
%Cálculo de estabilidad
%primero, obtenemos los autovalores de la matriz A:
autovalores=eig(A); %obtendremos 2 autovalores al ser una matriz 2x2
%creamos el programa que imprima en pantalla como es el sistema:
if isreal(autovalores(1)) && (autovalores(1)<0 && autovalores(2)<0)
fprintf('Sistema estable, con autovalores reales\n')
elseif ~isreal(autovalores(1))&& (real(autovalores(1))<0 && real(autovalores(2))<0)
fprintf('Sistema estable, con autovalores complejos conjugados\n')
else
fprintf('sistema inestable\n')
end
%Con esto queda demostrada la estabilidad del sistema, y finaliza el código
%del ejercicio.
Para el ejercicio, una vez simulado, hemos obtenido el siguiente resultado: “Sistema estable, con autovalores reales”, ya que los autovalores de la matriz son -0.2192 y
-0.2808, lo cual nos dice también de forma teórica que la estabilidad del sistema está garantizada.
Nota: De encontrar algún error en los cálculos, desarrollo, o simulaciones, puede corregirlos directamente (esto es un wiki [1]) o mandar un correo a vfernandez.fernandez AT alu.uhu.es para corregirlo lo mas rápido posible.
Simulacines y cálculos realizados por:
Victor Fernández Fernández
Carlos Javier Marín Mallo
Cristóbal Domínguez Blanco
Enlaces:
[1] http://es.wikipedia.org/wiki/Wiki