Ejercicio 1

a) Resolver la siguiente ecuación en diferencias, siendo u(k) una entrada impulsiva (delta de Kronecker [1]):

$y(k)=0.5 y(k-1) - 0.25 y(k-3) - u(k) -1.5 u(k-1) + 2 u(k-2)$

b) Obtener $y(k)$ mediante la simulación de la ecuación en diferencia (comando filter), mediante la función de transferencia (comando impulse) y mediante la resolución de la ecuación en diferencias (programando la solución de dicha ecuación).

c) Calcular $y(\infty)$ mediante el teorema del valor final y comprobar con la solución obtenida en el apartado anterior, haciendo $\lim_{ k \rightarrow \infty} \; y(k)$, que es resultado es correcto.

Resolución del apartado a):

Haciendo la transformada $\mathbf{Z}$ a la ecuación en diferencias anterior, obtenemos:

$Y(z)=0.5 z^{-1} Y(z) - 0.25 z^{-3} Y(z) - U(z) - 1.5 z^{-1} U(z) + 2 z^{-2}U(z)$

$Y(z) (1 - 0.5 z^{-1} + 0.25 z^{-3}) = U(z) (-1 - 1.5 z^{-1} + 2 z^{-2})$

$Y(z)=\dfrac{(-1 - 1.5 z^{-1} + 2 z^{-2})}{(1 - 0.5 z^{-1} + 0.25 z^{-3})} U(z)$

Como $u(k) = \delta (k)$ tenemos que $U(z) = 1$. Por lo tanto:

$ Y(z) = \dfrac{(-1 - 1.5 z^{-1} + 2 z^{-2})}{(1 - 0.5 z^{-1} + 0.25 z^{-3})} = \dfrac{-z^3-1.5z^2+2z}{z^3-0.5z^2+0.25}$

Para obtener $y(k)$ debemos calcular $\mathbf{Z^{-1}}\left \{ Y(z) \right \}$, para ello empezaremos obteniendo la descomposición en fracciones simples de $\dfrac{Y(z)}{z}$.

Las raices de la expresión $1 - 0.5 z^{-1} + 0.25 z^{-3} = 0$ son: $\left \{ \begin{array}{l}z = 0.5 +- 0.5j \\ z = 0.5\end{array} \right.$

$\dfrac{Y(z)}{z} = \dfrac{-z^2-1.5z^1+2}{z^3-0.5z^2+0.25} = \dfrac{A}{(z+0.5)} + \dfrac {Bz+C}{(z-0.5-0.5j)(z-0.5+0.5j)} = \dfrac{A}{(z+0.5)} + \dfrac {Bz+C}{(z-0.5)^2 + {0.5}^2}$

Como A es el residuo de una raiz real simple, podemos calcularlo como:

$\left. A = \dfrac{(-z^2-1.5z^1+2)}{(z+0.5)((z-0.5)^2 + {0.5}^2)}(z+0.5) \right | _ {z=-0.5} = \dfrac {-(-0.5)^2-1.5 (-0.5)+2}{(-0.5-0.5)^2+{0.5}^2}= 2$

Para calcular B y C podemos sumar la expresión $\dfrac{Y(z)}{z}$ y compararla con la original:

$\dfrac{Y(z)}{z} = \dfrac{A(z^2-z+0.5)+(Bz+C)(z+0.5)}{(z+0.5)((z-0.5)^2 + {0.5}^2)} = \dfrac{A(z^2-z+0.5)+Bz^2+0.5Bz+Cz+0.5C}{z^3-0.5z^2+0.25}$

Como los denominadores son idénticos (debe ser siempre así), comparamos los numeradores:

${-z^2-1.5z^1+2} = z^2(A+B) + z (-A+0.5B+C) + 0.5(A+C)$

Comparando término a término, debe cumplirse:

$\begin{array}{rcl}-1 &=& A+B \\ -A+0.5B+C &=& -1.5 \\ 0.5(A+C)&=&2 \end{array}$

Tenemos 3 ecuaciones con 3 incógnitas, por lo que podemos resolver A, B y C. Como A ya lo hemos calculado antes, A=2, podemos obtener B y C despejando:

$ B= -1-A = -1 -2 = -3$
$C= \dfrac {2-0.5A}{0.2} = \dfrac {2-0.5 \cdot 2}{0.2} = 2$

Se puede comprobar que $-A+0.5B+C = -2+0.5 \cdot (-3) + 2 = 1.5$

Por lo tanto,

$\dfrac {Y(z)}{z} = \dfrac{2}{(z+0.5)} + \dfrac {-3z+2}{(z-0.5)^2 + {0.5}^2} \Rightarrow Y(z) = \dfrac{2z}{(z+0.5)} + \dfrac {-3z^2+2z}{(z-0.5)^2 + {0.5}^2}$

La descomposición en fracciones simples también puede realizarse mediante el comando residue de MATLAB. Para ello tecleamos:

B=[-1,-1.5,2]; A=[1,-0.5,0,0.25]; % Polinomios numerador y denominador de Y(z)/z
[R,P,K]=residue(B,A)

Que nos retorna:

R =

-1.5 - 0.5i
-1.5 + 0.5i
2

P =

0.5 + 0.5i
0.5 - 0.5i
-0.5

K =

[]

Por lo tanto la descomposición en fracciones simples es:

$\dfrac {Y(z)}{z} = \dfrac {(-1.5-0.5i)}{(z-0.5-0.5j)} + \dfrac{(-1.5+0.5i)}{(z-0.5+0.5j)} + \dfrac{2}{(z+0.5)}$

Las dos primeras fracciones tienen residuos y polos complejos, con lo que no nos servirán para aplicar las tablas de transformadas. Para corregir esto debemos realizar la suma de dichas fracciones. Podemos hacerlo con MATLAB:

num = R(1)*[1,-P(2)]+R(2)*[1,-P(1)]

Cuyo resultado es [3,2], esto es, $3z+2$.

El denominador podemos hacerlo como "suma por diferencia, diferencia de cuadrados":

$(z-0.5-0.5j)(z-0.5+0.5j) = (z-0.5)^2 + {0.5}^2$

Es decir, obtenemos exactamente la misma expresión que antes:

$\dfrac {Y(z)}{z} = \dfrac{2}{(z+0.5)} + \dfrac {-3z+2}{(z-0.5)^2 + {0.5}^2} \Rightarrow Y(z) = \dfrac{2z}{(z+0.5)} + \dfrac {-3z^2+2z}{(z-0.5)^2 + {0.5}^2}$

Una vez descompuesta Y(z) en fracciones simples, podemos buscar cada una de estas en las tablas de transformadas para realizar la transformada $\mathbf{Z^{-1}}$:

$\mathbf{Z^{-1}}\left \{ \dfrac{2}{(z+0.5)} \right \} = 2(-0.5)^k$

Para obtener $\mathbf{Z^{-1}}\left \{ \dfrac{-3z^2+2z}{(z-0.5)^2+0.5^2} \right \}$ debemos realizar algunas operaciones previamente:

Si la parte real del polo es $\sigma = -0.5$, y la parate imaginaria $\omega = 0.5$,

el módulo es $c = \sqrt {\sigma ^2 + \omega ^2} = \sqrt {(-0.5)^2 + 0.5^2} = sqrt{0.5}$.

$sen(b) = \omega / c = 0.5 / \sqrt{0.5} = \sqrt{0.5}$,

$cos(b) = \sigma / c = 0.5 / \sqrt{0.5} = \sqrt{0.5}$

$b = arccos(\sqrt{0.5})$

Necesitamos obtener un numeradr igual a $z^2 -c \cdot z \cdot cos(b) = z^2 - \sqrt{0.5} \cdot z \cdot \sqrt{0.5} = z^2 -0.5 z$ para obtener una expresión de la forma $c^k\; cos(bk)$, y un numerador igual a $c \cdot z \cdot sen(b) = \sqrt{0.5} \cdot z \cdot \sqrt{0.5} = 0.5 z$ para obtener una expresión de la forma $c^k\; sen(bk)$.

$\mathbf{Z^{-1}}\left \{ \dfrac{-3z^2+2z}{(z-0.5)^2+0.5^2} \right \} = (-3) \mathbf{Z^{-1}}\left \{\dfrac{z^2-\dfrac {2}{3}z}{(z-0.5)^2+0.5^2} \right \} = (-3) \mathbf{Z^{-1}}\left \{\dfrac{z^2 -0.5z+0.5z-\dfrac {2}{3}z}{(z-0.5)^2+0.5^2} \right \} =$

$= -3 \mathbf{Z^{-1}}\left \{\dfrac{z^2 -0.5z}{(z-0.5)^2+0.5^2} \right \}+ \mathbf{Z^{-1}}\left \{ \dfrac{0.5z}{(z-0.5)^2+0.5^2}\right \}$

Ya tenemos las 2 expresiones buscadas, con lo que podemos calcular la transformada $\mathbf{Z^{-1}}$de cada una de ellas:

$-3 \mathbf{Z^{-1}}\left \{\dfrac{z^2 -0.5z}{(z-0.5)^2+0.5^2} \right \} = (-3)\sqrt{0.5}^k\; cos(bk)$

$\mathbf{Z^{-1}}\left \{ \dfrac{0.5z}{(z-0.5)^2+0.5^2}\right \} = \sqrt{0.5}^k\; sen (bk)$

Con este paso ya hemos concluido y podemos poner la expresión definitiva de y(k):

$y(k) = 2 (-0.5)^k + 0.5^{k/2} \left ( sen(bk)-3cos(bk) \right )$, siendo $b = arccos(\sqrt{0.5})$.

Resolución del apartado b):

En primer lugar vamos a realizar la simulación creando la funcíón de transferencia mediante el comando de Matlab "tf".

El comando tf crea una función de transferencia con los exponentes positivos a partir de los coeficientes que acopañan a Z en el numerador y el denominador.
La función de transferencia ya la tenemos calculada anteriormente:

$ G(z) =\dfrac{-z^3-1.5z^2+2z}{z^3-0.5z^2+0.25}$

Por lo que los coeficientes del numerador y denominador quedarían así:

Numerador --> [-1, 1.5, 2, 0]

Denominador-->[1, -0.5, 0, 0.25]

La función tf necesita un tercer parámetro que se corresponde con el periodo de muestreo. En nuestro caso no tendremos periodo de muestreo y lo indicaremos con un vector vacio [] como tercer parámetro.

La función quedaría de la siguiente forma:

G= tf([-1, 1.5, 2, 0], [1, -0.5, 0, 0.25], []);

Para simular esta función con una entrad impulso usamos el comando de Matlab "impulse", al que pasamos la función G como parámetro.

[y1,k]= impulse(G);

y1 contendrá la salida del sistema tras aplicarle la función impulso como entrada.

k tiene un vector de coordenadas en el eje X con una serie de valores que da Matlab para ajustar la gráfica de una forma correcta.

A continuación realizaremos la misma simulación con el comando "filter"

El comando Filter de Matlab se utiliza para crear secuencias de ponderación. Sus tres parámetros son el vector A de constantes que acompañan a las Y(k), el vector B de constantes que acompañan a las U(k) y un tercer vector como entrada al sistema.

En nuestro caso el vector de entrada será una delta de Kronecker. Para simularla crearemos un vector con todas las componentes a cero excepto la primera, simulando el comportamiento de la delta.

[1 0 0 0 0 0 0 0 0 0 0 .....]

Para ajustar el tamaño del vector en todas las representaciones utilizaremos el vector k obtenido con tf.

delta=zeros(size(k));

delta(1)=1;

 

A continuación creamos los vectores con los coeficientes, tomándolos directamente de la ecuación en diferencias después de agrupar las Y(k) y U(k) a un lado y a otro de la igualdad:

$$y(k)-0.5 y(k-1) +0.25 y(k-3) =- u(k) -1.5 u(k-1) + 2 u(k-2)$$

B=[-1, -1.5, 2];

A=[1, -0.5, 0, 0.25]

Para simular capturamos en y2 los valores de la salida del sistema.

y2=filter(B,A,delta);

La tercera simulación la realizamos con la ecuación obtenida en el apartado A de forma manual.

b=arcos(sqrt(0.5));

y3=2*(-0.5).^k+0.5.^(k/2).*(-3*cos(b*k)+sin(b*k));

 

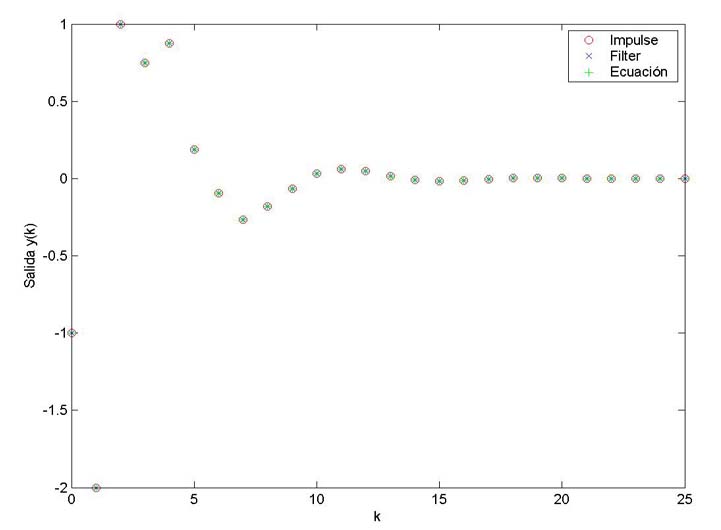
Instrucciones en Matlab

%funcion de transferencia
G=tf([-1, -1.5, 2, 0],[1,-0.5,0,0.25],[]);
[y1,k]=impulse(G);
%funcion en diferencias
delta=zeros(size(k));delta(1)=1;
B=[-1,-1.5,2];
A=[1,-0.5,0,0.25];
y2=filter(B,A,delta);
%funcion calculada
b=acos(sqrt(0.5));
y3=2*(-0.5).^k+0.5.^(k/2).*(-3*cos(b*k)+sin(b*k));

plot(k,y1,'ro');
hold on
plot(k,y2,'bx');
plot(k,y3,'g+');

xlabel('k'),ylabel('Salida y(k)')
legend('Impulse','Filter','Ecuación')

Resolución del apartado c):

Haciendo el límite a y(k) obtenida en el apartado a) tenemos:

$\lim_ {k \rightarrow \infty}\, y(k) = \lim_ {k \rightarrow \infty} \, 2(-0.5)^k + 0.5^{k/2} \left ( sen(bk)-3cos(bk) \right ) = 0.$
Es 0 porque tanto $0.5^k$ como $0.5^{k/2}$ tienden a 0 al aumentar k, y la expresión formada por el seno y el coseno está acotada.

Aplicando el Teorema del Valor Final:

$y(\infty) = \lim_ {z \rightarrow 1} {\dfrac {(z-1)}{z}\, Y(z)} = \lim_ {z \rightarrow 1} \, \dfrac {(z-1)}{z} \, \dfrac{(-z^3-1.5z^2+2z)}{(z^3-0.5z^2+0.25)} = \dfrac{0 (-1-1.5+2)}{1 (1-0.5+0.25)} = 0$

Como es lógico se obtiene el mismo resultado que además coincide con el de la simulación.

Ejercicio 2

a) Resolver la siguiente ecuación en diferencias, siendo u(k) una entrada escalon (u(k)={1,1,1...}):

$y(k)=0.5 y(k-1)-0.12 y(k-2) +0.008 y(k-3) +u(k-2) +2 u(k-3)$

b) Obtener $y(k)$ mediante la simulación de la ecuación en diferencia (comando filter), mediante la función de transferencia (comando step) y mediante la resolución de la ecuación en diferencias (programando la solución de dicha ecuación).

c) Calcular $y(\infty)$ mediante el teorema del valor final y comprobar con la solución obtenida en el apartado anterior, haciendo $\lim_{ k \rightarrow \infty} \; y(k)$, que es resultado es correcto.

Resolución del apartado a):

Haciendo la transformada $\mathbf{Z}$ a la ecuación en diferencias anterior, obtenemos:

$Y(z)=0.5 z^{-1} Y(z) - 0.12 z^{-2} Y(z) + 0.008 z^{-3} Y(z) + U(z)z^{-2} + 2 U(z)z^{-3}$

$Y(z) (1 - 0.5 z^{-1} +0.12z^{-2} -0.008z^{-3}) = U(z) (z^{-2} + 2 z^{-3})$

$Y(z)=\dfrac{(z^{-2}+ 2 z^{-3})}{(1 - 0.5 z^{-1} + 0.12 z^{-2} -0.008z^{-3})} U(z)$

Como $u(k) =\{1,1,1,..\} $ tenemos que $U(z) = \dfrac{(z)}{(z-1)}$. Por lo tanto:

$ Y(z) = [\dfrac{(z^{-2}+ 2 z^{-3})}{(1 - 0.5 z^{-1} + 0.12 z^{-2} -0.008z^{-3})}. \dfrac{z^3}{z^3}] \dfrac{z}{(z-1)} = \dfrac{-z+2}{z^3-0.5z^2+0.12z-0.008} . \dfrac{z}{(z-1)}$

- Notas: Solo se ha multiplicado el primer termino por $\dfrac{z^3}{z^3}$ para pasar los exponentes a positivos, y no se ha efectuado la operación con $\dfrac{z}{(z-1)}$ con la idea de utilizar la z del numerador para el $\dfrac{Y(z)}{z}$ que veremos a continuación y el denominador como polo ya resuelto del sistema (asi ya tenemos calculado uno).

Para obtener $y(k)$ debemos calcular $\mathbf{Z^{-1}}\left \{ Y(z) \right \}$, para ello empezaremos obteniendo la descomposición en fracciones simples de $\dfrac{Y(z)}{z}$.

Las raices de la expresión $z^3 -0.5z^2 +0.12z -0.008 = 0$ son: $\left \{ \begin{array}{l}z = 0.2 +- 0.2j \\ z = 0.2\end{array} \right.$

$\dfrac{Y(z)}{z} = \dfrac{z+2}{(z-1)(z^3 -0.5z^2 +0.12Z -0.008)} = \dfrac{A}{(z-1)} + \dfrac {Bz+C}{(z-0.2-0.2j)(z-0.2+0.2j)} + \dfrac {D}{z-0.1} = \dfrac{A}{(z-1)} + \dfrac {Bz+C}{(z-0.2)^2 + {0.2}^2} + \dfrac{D}{z-0.1}$

Como A es el residuo de una raiz real simple, podemos calcularlo como:

$\left. A = \dfrac{(z+2)}{(z-1)((z-0.2)^2 + {0.2}^2)(z-0.1)}(z-1) \right | _ {z=1} = \dfrac {3}{((1-0.2)^2+{0.2}^2)(0.9)}\simeq 4.9$

Con D pasa lo mismo, asi que lo calculamos de la siguiente manera también:

$\left. D = \dfrac{(z+2)}{(z-1)((z-0.2)^2 + {0.2}^2)(z-0.1)}(z-0.1) \right | _ {z=0.1} = \dfrac {2.1}{(-0.9)((0.1-0.2)^2+{0.2}^2)}\simeq 46.6$

Para calcular B y C podemos sumar la expresión $\dfrac{Y(z)}{z}$ y compararla con la original:

$\dfrac{Y(z)}{z} = \dfrac{A((z-0-2)^2 + 0.2^2)(z-0.1) + (Bz+C)(z-1)(z-0.1) + D((z-0.2)^2+0.2^2)(z-1)}{(z-1)((z-0.2)^2+0.2^2)(z-0.1)}$

Comparando término a término, debe cumplirse:

$\begin{array}{rcl}A+B+D &=&0\\ -0.5A-1.1B+C-0.6D &=& 0 \\ 0.12A + 0.1B - 1.1C + 0.48D&=&1 \\-0.08A + 0.1C -0.08D &=&2 \end{array}$

De la ultima sacamos C

$ 1.1C=2-0.04*46.6-0.008*4.9$
$C= \dfrac{2 -3.73 -0.0392}{0.1} =-17.69$

Con C deberiamos obtener de las otras ecuaciones que:

$D=41.93 $

Por lo tanto,

$\dfrac {Y(z)}{z} \simeq \dfrac{4.9}{(z-1)} + \dfrac {42z-17}{(z-0.2)^2 + {0.2}^2} + \dfrac{46.6}{z-0.1}\Rightarrow Y(z) \simeq \dfrac{4.9z}{(z-1)} + \dfrac {42z^2-17z}{(z-0.2)^2 + {0.2}^2} + \dfrac{46.6z}{z-0.1}$

 

 

*La descomposición en fracciones simples también puede realizarse mediante el comando residue de MATLAB. Para ello tecleamos:

B=[1,2]; A=conv([1,-0.5,0.12,-0.008],[1,-1]); % Polinomios numerador y denominador de Y(z)/z
[R,P,K]=residue(B,A)

Que nos retorna:

R =

4.9020

20.8824 + 21.4706i

20.8824 - 21.4706i

46.6667

P =

1

0.2 + 0.2i

0.2 - 0.2i

0.1

K =

[]

Por lo tanto la descomposición en fracciones simples es:

$\dfrac {Y(z)}{z} = \dfrac {(4.9020)}{(z-1)} + \dfrac{(20.8824+21.4706j)}{(z-(0.2+0.2j))} + \dfrac{(20.8824-21.4706j)}{(z-(0.2-0.2j))} + \dfrac{46.6667}{z-0.1}$

Las dos primeras fracciones tienen residuos y polos complejos, con lo que no nos servirán para aplicar las tablas de transformadas. Para corregir esto debemos realizar la suma de dichas fracciones. Podemos hacerlo con MATLAB:

num = R(2)*[1,-P(3)]+R(3)*[1,-P(2)]

Cuyo resultado es [41.7647,-16.9411], esto es, $41.7647z-16.9411$.

El denominador podemos hacerlo como "suma por diferencia, diferencia de cuadrados":

$(z-0.2-0.2j)(z-0.2+0.2j) = (z-0.2)^2 + {0.2}^2$

den = conv([1,-P(2),[1,-P(3)]) =[1,-0.4,0.08]

Es decir, obtenemos exactamente la misma expresión que antes:

$\dfrac {Y(z)}{z} = \dfrac{4.9020}{(z-1)} + \dfrac {41.7647z-16.9411}{(z-0.2)^2 + {0.2}^2} + \dfrac{-46.6667}{z-0.1} \Rightarrow Y(z) = \dfrac{4.9020z}{(z-1)} + \dfrac {41.7647z^2-16.9411z}{(z-0.2)^2 + {0.2}^2} + \dfrac{-46.6667z}{z-0.1}$

Una vez descompuesta Y(z) en fracciones simples, podemos buscar cada una de estas en las tablas de transformadas para realizar la transformada $\mathbf{Z^{-1}}$:

$\mathbf{Z^{-1}}\left \{ \dfrac{4.902z}{(z-1)} \right \} = 4.902(1)^k$

$\mathbf{Z^{-1}}\left \{ \dfrac{-46.6667z}{(z-0.1)} \right \} = -46.6667(0.1)^k$

Para obtener $\mathbf{Z^{-1}}\left \{ \dfrac{41.7647z^2 - 16.9411z}{(z-0.2)^2+0.2^2} \right \}$ debemos realizar algunas operaciones previamente:

Si la parte real del polo es $\sigma = 0.2$, y la parate imaginaria $\omega = 0.2$,

el módulo es $c = \sqrt {\sigma ^2 + \omega ^2} = \sqrt {(0.2)^2 + 0.2^2} = sqrt{0.08}$.

$sen(b) = \omega / c = 0.2 / \sqrt{0.5} = 2.5\sqrt{0.08}$,

$cos(b) = \sigma / c = 0.2 / \sqrt{0.2} = 2.5\sqrt{0.08}$

$b = arccos(\sqrt{0.08})$

Necesitamos obtener un numeradr igual a $z^2 -c \cdot z \cdot cos(b) = z^2 -\sqrt{0.08} \cdot z \cdot 2.5\sqrt{0.08} = z^2 -0.2 z$ para obtener una expresión de la forma $c^k\; cos(bk)$, y un numerador igual a $c \cdot z \cdot sen(b) = \sqrt{0.08} \cdot z \cdot2.5 \sqrt{0.08} = 0.2 z$ para obtener una expresión de la forma $c^k\; sen(bk)$.

$\mathbf{Z^{-1}}\left \{ \dfrac{41.7647z^2 - 16.9411z}{(z-0.2)^2+0.2^2} \right \}\simeq \mathbf{Z^{-1}}\left \{\dfrac{42z^2-17z}{(z-0.2)^2+0.2^2} \right \} =(42) \mathbf{Z^{-1}}\left \{\dfrac{z^2-0.4z}{(z-0.2)^2+0.2^2} \right \} =$

$= (42) \mathbf{Z^{-1}}\left \{\dfrac{z^2 -0.2z -0.2z }{(z-0.2)^2+0.2^2} \right \}= (42) \mathbf{Z^{-1}}\left \{\dfrac{z^2 -0.2z }{(z-0.2)^2+0.2^2} \right \}-(42) \mathbf{Z^{-1}}\left \{\dfrac{0.2z }{(z-0.2)^2+0.2^2} \right \}$

Ya tenemos las 2 expresiones buscadas, con lo que podemos calcular la transformada $\mathbf{Z^{-1}}$de cada una de ellas:

$(42) \mathbf{Z^{-1}}\left \{\dfrac{z^2 -0.2z }{(z-0.2)^2+0.2^2} \right \}= (42)\sqrt{0.08}^k\; cos(bk)$

$(-42) \mathbf{Z^{-1}}\left \{\dfrac{0.2z }{(z-0.2)^2+0.2^2} \right \}= (-42)\sqrt{0.08}^k\; sen (bk)$

Con este paso ya hemos concluido y podemos poner la expresión definitiva de y(k):

$y(k) = 4.902 - 46.6667 (0.1)^k + 0.08^{k/2} 42 \left ( cos(bk)-sen(bk) \right )$, siendo $b = arccos(\sqrt{0.08})$.

Resolución del apartado b):

En primer lugar vamos a realizar la simulación creando la funcíón de transferencia mediante el comando de Matlab "tf".

El comando tf crea una función de transferencia con los exponentes positivos a partir de los coeficientes que acopañan a Z en el numerador y el denominador.
La función de transferencia ya la tenemos calculada anteriormente:

$ G(z) =\dfrac{z+2}{z^3-0.5z^2+0.12z-0.008}$

Por lo que los coeficientes del numerador y denominador quedarían así:

Numerador --> [1,2]

Denominador-->[1, -0.5,0.12, -0.008]

La función tf necesita un tercer parámetro que se corresponde con el periodo de muestreo. En nuestro caso no tendremos periodo de muestreo y lo indicaremos con un vector vacio [] como tercer parámetro.

La función quedaría de la siguiente forma:

G= tf([1,2], [1, -0.5,0.12, -0.008], []);

Para simular esta función con una entrada escalon usamos el comando de Matlab "step", al que pasamos la función G como parámetro.

[y1,k]= step(G);

y1 contendrá la salida del sistema tras aplicarle la función impulso como entrada.

k tiene un vector de coordenadas en el eje X con una serie de valores que da Matlab para ajustar la gráfica de una forma correcta.

A continuación realizaremos la misma simulación con el comando "filter"

El comando Filter de Matlab se utiliza para crear secuencias de ponderación. Sus tres parámetros son el vector A de constantes que acompañan a las Y(k), el vector B de constantes que acompañan a las U(k) y un tercer vector como entrada al sistema.

En nuestro caso el vector de entrada será una secuencia escalón. Para simularla crearemos un vector con todas las componentes a 1,simulando el comportamiento de la delta.

[1 1 1 1 .....]

Para ajustar el tamaño del vector en todas las representaciones utilizaremos el vector k obtenido con tf.

escalon=ones(size(k));

A continuación creamos los vectores con los coeficientes, tomándolos directamente de la ecuación en diferencias después de agrupar las Y(k) y U(k) a un lado y a otro de la igualdad:

$y(k)-0.5 y(k-1) +0.12 y(k-2)-0.008y(k-3) =u(k-2) + 2 u(k-3)$

B=[0,1,2];

A=[1,-0.5,0.12,-0.008]

Para simular capturamos en y2 los valores de la salida del sistema.

y2=filter(B,A,escalon);

La tercera simulación la realizamos con la ecuación obtenida en el apartado A de forma manual.

b=arcos(sqrt(0.08));

y3=4.902+42*(0.08).^(k/2).*cos(b*k)-42*(0.08).^(k/2).*1.03.*sin(b*k)-46.6667*0.1.^k;

Instrucciones en Matlab

clc,clear all,close all %%pagina CC-11 ejercicio b)
G=tf([1,2],[1,-0.5,0.12,-0.008],[]); %de la G(z) funcion de transferencia, ke es Y(Z)/U(Z)
k=0:20;
[y1,k]=step(G,k);%le damos la entrada.
entradaescalon=ones(size(k));
A=[1,-0.5,0.12,-0.008];%de la ecuacion de diferencias lo ke acompaña a la Y
B=[0,1,2];%lo que acompaña a la U
y2=filter(B,A,entradaescalon);

b=pi/4;%tenemos como raiz cuadrada de 0.08 de forma manual pero la ekivalencia es pi/4 y asi no perdemos tanta precision

y3=4.902+42*(0.08).^(k/2)*( cos(b*k)-sin(b*k) )-46.6667*0.1^k;

plot(k,y1,'bo',k,y2,'r+',k,y3,'.c')
xlabel('k'),ylabel('Salida y(k)')
legend('Step','Filter','Ecuación')

Grafica del ejercicio2:

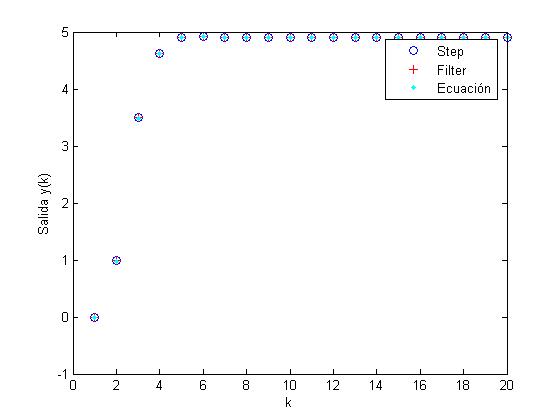
Resolución del apartado c):

Haciendo el límite a y(k) obtenida en el apartado a) tenemos:

$\lim_ {k \rightarrow \infty}\, y(k) = \lim_ {k \rightarrow \infty} \, 4.902-46.6667*0.1^{k/2} \left ( -sen(bk)+cos(bk) \right ) = 4902.$
Es 4902 porque $0.1^k$ tiende a 0 al aumentar k, y la expresión formada por el seno y el coseno está acotada.

Aplicando el Teorema del Valor Final:

$y(\infty) = \lim_ {z \rightarrow 1} {\dfrac {(z-1)}{z}\, Y(z)} ={\dfrac{(z-1)}{z}.\dfrac{z}{z-1}.\dfrac{z+2}{z^3-0.5z^2+0.12z-0.008} \simeq 4.902}$