Práctica 4: Determinación del coeficiente adiabático del aire.

Introducción

Las transformaciones adiabáticas son de gran importancia en la atmósfera debido a que, por una parte, ciertas evoluciones del aire atmosférico son adiabáticas (cuando el aire asciende o desciende “rápidamente” y con una cantidad de vapor de agua alejada de la saturación, es decir, poseyendo una humedad relativa baja) mientras que, por otra parte, a partir de los resultados obtenidos para evoluciones adiabáticas pueden obtenerse resultados para evoluciones politrópicas conocido el exponente politrópico o el calor específico de la transformación¹.

Fundamento teórico

Supongamos que se tiene un recipiente que contiene cierto gas y que dicho recipiente termina en su parte superior en un tubo vertical de forma cilíndrica. Si por el tubo se deja caer una pieza cilíndrica que se ajuste con precisión al tubo de forma que no haya fuga de gases entre la pieza y el tubo, ésta empezará a oscilar alrededor de una posición de equilibrio. Estas oscilaciones pueden entenderse desde el punto de vista cualitativo teniendo en cuenta que a medida que la pieza cae por el interior del tubo, disminuye el volumen del gas que se encuentra en el interior del recipiente, aumentando por lo tanto su presión. Cuando el aumento de presión es lo suficientemente grande, la pieza se detiene y empieza a ascender. Al sobrepasar la pieza durante su ascenso su posición inicial, la presión del gas disminuye. Cuando la presión es lo suficientemente pequeña, la pieza detiene su ascenso y empieza a caer, completando el ciclo. Puede demostrarse que la aceleración a la que está sometida la pieza, sin más que aplicar la segunda ley de Newton, viene dada por la siguiente ecuación:

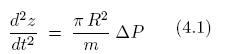
donde m es la masa de la pieza cilíndrica, R es su radio, 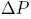es la variación de presión producida en el gas debido a las oscilaciones de la pieza y z es la coordenada correspondiente a un eje vertical, orientado hacia arriba y cuyo origen coincide con el punto en el cual se ha abandonado la pieza.

Por otra parte, para una evolución adiabática de coeficiente , se cumple que:

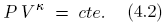
Derivando esta expresión, puede obtenerse que:

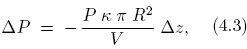
donde se ha tenido en cuenta,

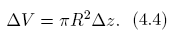
Si suponemos que el proceso de oscilación es lo suficientemente rápido para que no tenga lugar intercambio de calor podemos sustituir en la expresión (4.1) obteniéndose que:

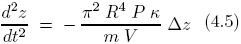
Esta ecuación describe un movimiento armónico simple (F = -K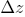) de frecuencia angular:

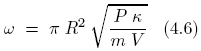
A partir de esta expresión y teniendo en cuenta 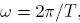, siendo T el periodo de la oscilación, puede despejarse el coeficiente adiabático K :

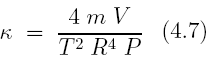
donde P es la presión de equilibrio en el interior del recipiente. Esa presión viene dada por:

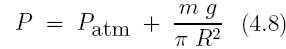
El valor de k obtenido en la práctica puede compararse con el que predice la teoría cinética de los gases:

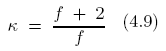
donde f es el número de grados de libertad de las moléculas del gas:

• gases monoatómicos: f=3 --> k=1.67
• gases diatómicos: f=5 --> k=1.40
• gases poliatómicos: f=6 --> k=1.33

Para el aire se obtiene que k=1.38 ± 0.08.

Objetivos

El objetivo de esta práctica es la medición del coeficiente adiabático del aire, K, y al mismo tiempo la famialiarización del alumno con un típico proceso adiabático en la atmósfera.