

Apuntes de la asignaturas Automática I y Automática II de Ingeniería Técnica Industrial, especialidad electrónica industrial.
Autores:
Escuela Técnica Superior de Ingeniería [2], Universidad de Huelva [3]
La automática la define el diccionario de la Real Academia Española (RAE) como la ciencia que trata de sustituir en un proceso el operador humano por dispositivos mecánicos o electrónicos.
El término control tiene muchos significados dependiendo de la comunidad donde se aplique. Desde la perspectiva de la automática y siguiendo también la definición del RAE, hace referencia a la regulación, manual o automática, sobre un sistema. Esta regulación tiene por objeto conseguir unas condiciones determinadas de funcionamiento del sistema bajo control. Por tanto, y desde el punto de vista de esta asignatura, el término control incluye lazos de realimentación en amplificadores electrónicos, controladores de puntos de consigna en procesos químicos, ordenadores de vuelo de aviones, controladores de tráfico en Internet (routers), etc. El concepto de control va acaparando cada vez aplicaciones más sofisticadas y novedosas en los campos de vehículos y robots autónomos, sistemas biológicos, cirugía, tele-asistencia, economía, etc.
En la Figura 1.1 se muestra el esquema de un sistema controlado por computador. El cuadro superior en línea discontinua representa la dinámica del proceso (quiere decir el conjunto de ecuaciones que reflejan su comportamiento temporal) que se quiere controlar. Los actuadores (también denominados accionadores) son los elementos (usualmente de potencia: motores, electroválvulas, etc.) que actúan sobre el sistema condicionando su funcionamiento. El sistema bajo control o planta (en control, al sistema a controlar se le suele denominar planta) está representado por su modelo dinámico (modelo matemático escrito de forma adecuada para poder aplicar las técnicas de Ingeniería de Control). A la salida de la planta los sensores miden el estado de las variables que han de ser controladas (presión, temperatura, velocidad, etc.). Tanto el ruido en la actuación y la medida (el ruido es en general una mala concreción en la señal, bien porque está contaminada con ruido interno o externo, o porque no se tiene certeza de su valor y sólo se conoce hasta una precisión) como las posibles perturbaciones sobre la planta (una racha de viento en el control del rumbo de un avión por ejemplo) han de ser consideradas en el proceso de control. En este apartado de ruidos y perturbaciones habría que tener también en cuenta las posibles incertidumbres en la dinámica de la planta (errores en sus parámetros, efectos no modelados, etc.). Es deseable que el sistema de control sea robusto frente a todos estos efectos perniciosos. Esto es, esté preparado para soportarlos.
El cuadro inferior en línea discontinua de la Figura 1.1 representa el controlador. Éste sensa (mide) a la salida de la planta la/s variable/s que se desean tener bajo control. La medida, después de pasar por un filtro para acondicionarla, entra en un convertidor A/D, ya que el algoritmo que realiza el control (ley de control) está implementado en un computador. La señal de control que produce el algoritmo después de analizar la entrada que le ha llegado, se dirige a un convertidor D/A, ya que normalmente los actuadores funcionan con señales analógicas. Nótese que una señal de reloj sincroniza la operación de los convertidores y el procesado en el computador. También hay que tener en cuenta la entrada externa al computador, la cual permite cambiar parámetros y/o consignas en el algoritmo de control.
La palabra clave más importante del control es la realimentación. Nótese en la Figura 1.1 como los cuadros de línea discontinua que representan el proceso y el controlador están interconectados, de modo que la salida del primero se usa como entrada del segundo, creando de este modo un sistema en lazo cerrado.
 |
| Figura 1.1 |
El concepto central en control es el lazo de realimentación medida – computación – actuación. El primer objetivo a conseguir mediante el control es que la dinámica del sistema en lazo cerrado sea estable. Esto es, las perturbaciones acotadas han de producir como mucho errores acotados. Garantizada la estabilidad del sistema en lazo cerrado, el controlador ha de proveer otras características deseables como por ejemplo: respuesta rápida ante cambios en los puntos de consigna, rechazo o buena atenuación a las perturbaciones, etc. Las propiedades del controlador se establecen a partir de una amplia variedad de técnicas de modelado, análisis y síntesis, las cuales veremos durante el curso. Estas técnicas permiten capturar lo esencial de la dinámica del sistema así como explorar comportamientos del mismo en presencia de incertidumbres, ruido o fallos en los componentes.
La Ingeniería de Control es una disciplina de la ciencia que está muy conectada con otras que usa como herramientas: física (dinámica y modelado), matemáticas (algoritmia, análisis matemático, álgebra), computación (información y software), investigación operativa (optimización, probabilidad, teoría de juegos). No obstante lo anterior, debe quedar claro que tanto los objetivos como la aproximación al problema y su resolución son muy diferentes en la Ingeniería de Control respecto de las disciplinas anteriores.
Hoy en día, debido fundamentalmente a que las leyes de control se implementan en un computador (implementación software), el control y la ciencia de la computación están muy relacionados, sin embargo, debe quedar claro que tanto los algoritmos como el propio software son muy diferentes, debido a los requerimientos de la dinámica del sistema y a la naturaleza de implementaciones en tiempo real.
 |
| Figura 1.2 |
La realimentación tiene una serie de propiedades muy interesantes y útiles. Así por ejemplo permite diseñar sistemas precisos a partir de elementos imprecisos, estabilizar un sistema inestable o minimizar las perturbaciones externas sobre un sistema. A continuación se va a realizar un breve recorrido sobre ejemplos ilustrativos de a influencia de la realimentación en la consecución de hitos de control.
Primeros ejemplos tecnológicos
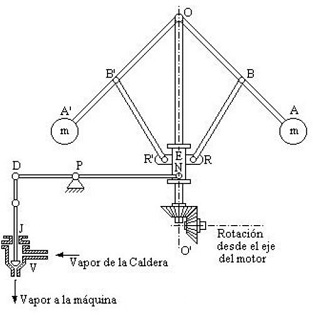
La proliferación de sistemas de control en la vida cotidiana ocurrió sobretodo a partir de la mitad de los años 50 del siglo pasado. No obstante, existen ejemplos aislados acontecidos mucho antes, como por ejemplo el regulador centrífugo o de bolas (inventado por el ingeniero inglés J. Watt en 1788, por lo que es también conocido como regulador de Watt), el cual (ver Figura 1.2) emplea la fuerza centrífuga originada por la velocidad de giro de las bolas del contrapeso para deslizar por un eje el mecanismo que acciona la válvula de admisión de vapor. Nótese como al estar obturado el vapor a la máquina ésta disminuirá la velocidad de rotación del eje del motor, lo cual hará que las bolas giren más despacio y tiendan a caer. Entonces, el casquillo que se desplaza por el eje será empujado hacia abajo dejando de obturar el paso de vapor a la máquina, con lo cual esta aumentará de nuevo su velocidad de giro. El regulador centrífugo es pues un controlador de la velocidad de giro de la máquina de vapor.
 |
 |
| (a) | (b) |
| Figura 1.3 | |
Otro ejemplo que, aunque más moderno que el anterior, es de finales del siglo XX, es el termostato utilizado para regular la temperatura de una vivienda, el cual fue inventado por Albert Butz en 1885 y cuya explotación comercial dio lugar a la compañía Honeywell. En la Figura 1.3 (a) puede verse un termostato de Honeywell del año 1953. En la Figura 1.3 (b) se muestra un termostato analógico de los más usuales que aún hoy pueden verse en edificios. Su funcionamiento está basado en la propiedad que presentan los metales de dilatarse al aumentar la temperatura. Se coloca un fleje con dos láminas unidas de dos metales con diferente coeficiente de dilatación (cobre e hierro por ejemplo). Cuando la temperatura aumenta, la lámina que se dilata más (en este caso la de cobre) se curva, ya que necesita más espacio, con lo cual se separan los contactos del fleje y se abre el circuito eléctrico. Esto detiene el sistema de calefacción hasta que la temperatura baje, el metal se contraiga, el fleje se estire y, como consecuencia, se cierre el circuito eléctrico que activa de nuevo la calefacción. Respecto del concepto de controlador, la lámina bimetálica actúa como tal y como sensor, ya que a partir de una temperatura de consigna fijada por el usuario mediante el mando (curvatura del fleje), el sistema la compara con la de la habitación a controlar (variable de salida); cuando hay diferencia se genera una señal de error que es realimentada para generar una señal de mando (control) que enciende o apaga la calefacción. Aunque el funcionamiento del termostato captura la esencia del control mediante realimentación, su mecanismo es demasiado simple e imperfecto (aunque útil), ya que existen retardos entre el sensor y la planta a controlar (habitación). Los termostatos de calidad actuales se anticipan apagando o encendiendo la calefacción antes que la señal de error cambie de signo, lo cual evita saltos de temperatura grandes así como ciclos de funcionamiento elevados de la máquina. Esta interacción entre la dinámica del proceso (la velocidad de calentamiento o enfriamiento de la habitación) y la operación del controlador es un elemento clave en el diseño de los sistemas de control actuales.
Con el transcurso del siglo XX se fueron desarrollando sistemas de control cada vez más sofisticados, como por ejemplo el control de crucero o controlador de velocidad para vehículos. Éste fue inventado en 1945 por el inventor ciego e ingeniero mecánico Ralph Teetor (ver Figura 1.4). Su idea nació de la frustración de ir en el vehículo con su abogado, quien frenaba y aceleraba continuamente según hablaba. El primer vehículo con el sistema de Teetor fue el Chrysler Imperial en 1958. Este sistema calculaba la velocidad sobre la carretera basándose en las rotaciones de un palier y usaba una bobina para variar la posición del acelerador según fuera necesario. Hoy en día los automóviles son quizás los sistemas que, siendo más cercanos al gran público, están dotados de más sistemas de control (control de crucero adaptativo1 [5] , control de tracción2 [6] , control de estabilidad3 [7] , control de emisión de gases, etc.).
| Figura 1.4 |
Generación y transporte de energía eléctrica
El control es una misión crítica en los sistemas de producción y transporte de energía eléctrica, de modo que las centrales eléctricas están dotadas de multitud de lazos de control para garantizar su correcto funcionamiento. El control es fundamental también en el transporte de la electricidad, ya que ésta ha de ser llevada hasta el último rincón donde es necesaria y con la potencia adecuada, pero la energía eléctrica tiene muy difícil almacenaje, con lo cual hay que adecuar lo más posible la generación al consumo. La gestión de la energía en la red eléctrica es un problema de control sencillo de resolver cuando hay un solo generador y un consumidor (caso de una vivienda aislada que se genera su propia electricidad por paneles fotovoltaicos por ejemplo), pero es muy complejo es un sistema altamente distribuido, donde hay muchos generadores, muchos más consumidores y largas distancias entre ellos. Para añadir aún más complejidad al problema del control de la red eléctrica, hay que tener en cuenta que la demanda en un punto o varios a la vez puede cambiar de forma rápida e impredecible. En la Figura 1.5 se muestra a modo de ejemplo el sistema eléctrico (enero de 2009) en alta tensión que circunda la ciudad de Huelva. En color rojo se dibujan las líneas de 400 KV, en verde las de 220 KV, en azul las de 132/110 KV y, en negro, las de menos de 110 KV. Las líneas discontinuas, sean del color que sean, representan líneas programadas o en construcción de la tensión correspondiente al color. Los puntos gruesos de color negro representan subestaciones eléctricas (al lado de las centrales sirven para elevar la tensión antes de transportarla, y al lado de las poblaciones para reducir la tensión con objeto de poder usarla), y los cuadros representan las centrales con su capacidad de producción en MW. Los rellenos de negro las térmicas clásicas, los que tienen la mitad rellena de negro eólicas y los de la mitad diagonal rellena de negro de ciclo combinado. El control del sistema eléctrico exige adecuar la producción de las centrales a las necesidades de los clientes (cargas) pasando por las subestaciones.
Caídas de árboles sobre líneas, vientos, rayos, fallos en equipos, etc., pueden ocasionar perturbaciones graves en el sistema eléctrico, por ello, deben haber sofisticados sistemas de control que eliminen o minimicen sus consecuencias para el usuario final. Dependiendo de la gravedad de la perturbación los diferentes niveles del control del sistema eléctrico actuarán reduciendo la tensión, dividiendo una red en subredes, desconectando líneas y usuarios, etc. El sistema eléctrico es pues un buen ejemplo de lo complicado que puede llegar a ser un sistema de control.
 |
| Figura 1.5 |
 |
| Figura 1.6 Fotografía original del primer vuelo con motor de la historia. A los mandos Orville Wright; a la derecha, su hermano Wilbur. 17 de diciembre de 1903. El vuelo fue sobre las playas de Kitty Hawk, Carolina del Norte. El aparato, en su primer despegue, recorrió 36 metros en 12 segundos. |
Aerospacial
La consecución de un control adecuado fue probablemente la llave que permitió a los hermanos Wright hacer volar un aparato a principios del siglo XX (ver Figura 1.6). De hecho, los hermanos Wright no se hicieron famosos por demostrar simplemente el vuelo con motor, sino por demostrar el vuelo con motor controlado. Su primer aeroplano incorporaba ya superficies de control (aletas verticales y alas de pato4 [8] ) así como alas adaptables que permitían al piloto controlar el vuelo. Realmente, un avión en vuelo es un sistema que tiende a hacerse inestable, con lo cual se necesita un sistema de control (el piloto cuando el vuelo es manual) que actúe de forma constante para que no caiga. A este primer vuelo controlado de 1903 le han seguido 100 años de éxitos continuos en la mejora de los sistemas de control de los aviones, los cuales han dado lugar a los aparatos comerciales y militares de hoy en día (ver Figura 1.7). En la Figura 1.7 (a) se muestra el Eurofighter, nacido de un consorcio anglo/alemán/italo/español. Es un avión de una maniobrabilidad extraordinaria (obsérvense sus alas de pato y de delta truncadas), para lo cual se diseñó inherentemente inestable; un cuádruple sistema de control digital da una estabilidad artificial al estar ajustando constantemente las superficies de control (Fly-by-wire5 [9] ). En la Figura 1.7 (b) se muestra el X-45 UCAV (Unmanned Combat Air Vehicle), un avión militar no tripulado estadounidense apto para volar a match 0,85 y capaz de transportar misiles. Tanto su longitud total como envergadura de alas están en torno a los 11 metros.
 |
 |
| (a) | (b) |
| Figura 1.7. Aviones militares modernos. (a) Eurofighter Typhoon. (b) Avión no tripulado X-45 J-UCAV. | |
El sector espacial es una de las puntas de lanza del desarrollo investigador en el ámbito del control, de hecho la carrera espacial tanto rusa como norteamericana han marcado hitos tecnológicos que luego han sido de aplicación a otros campos. Uno de los grandes retos científicos que afrontó la NASA desde mediados de los años 60 fue disponer de un transbordador espacial. Esto lo consiguió el 12 de abril de 1981 con el lanzamiento del primer sistema de transbordador espacial (en inglés: Space Transport System, STS o Space Shuttle), el Columbia (ver Figura 1.8 (a). Actualmente el uso del transbordador espacial está concentrado totalmente en el ensamblaje de la Estación Espacial Internacional (en inglés: International Space Station, ISS). El tiempo de vida de transbordadores espaciales de esta clase se espera que acabe a finales de 2010. Para entonces deberán ser substituidos por el vehículo Orion norteamericano y/o la nave rusa Kliper, de mucho menor coste que los transbordadores espaciales norteamericanos.
En este apartado merece un lugar especial la sonda espacial Voyager I, la cual fue lanzada el 5 de septiembre de 1977 y gracias a que ha superado con creces sus perspectivas iniciales de vida útil (fue diseñada inicialmente para visitar Júpiter y Saturno) es hoy en día el objeto hecho por el hombre más alejado de la Tierra. De hecho está atravesando la Heliopausa6 [10] a más de 16.000 millones de kilómetros del Sol. Cuando la Voyager I sobrepase la Heliopausa será el primer objeto de fabricación humana que abandone nuestro sistema estelar. Entonces los científicos obtendrán las primeras mediciones directas de las condiciones del espacio interestelar, las cuales podrían proveer pistas relevantes del origen y la naturaleza del universo. A esta distancia, las señales del Voyager I tardarán más de quince horas en alcanzar el centro de control en la Tierra. Voyager 1 tiene una trayectoria parabolica, y ha alcanzado velocidad de escape, lo que significa que su orbita no regresará nunca al Sistema solar interior. Esto es, vagará eternamente por el espacio enviando señales a la Tierra hasta que su sistema de energía se agote (sobre el año 2.025).
 |
 |
| (a) | (b) |
| Figura 1.8. Ingenios espaciales. (a) Lanzamiento del Columbia en 1981. (b) Sonda espacial Voyager I lanzada el 5 de septiembre de 1977. | |
Materiales y transformación
La industria química es responsable del auge considerable en el desarrollo de nuevos materiales, lo cual es clave en el desarrollo de nuestra sociedad. Además, tal como el nivel de exigencia de ésta aumenta, se hace necesario mejorar cada vez más la calidad de los productos fabricados minimizando todo tipo de riesgos, como los medioambientales por ejemplo, lo cual obliga a controles cada vez más precisos en esta industria7 [11]. Por otro lado, los procesos productivos se requieren que sean cada vez más eficientes energéticamente, lo cual ha dado lugar a los procesos de cogeneración8 [12]. Cada nuevo requerimiento añade complejidad al sistema de control de la planta industrial, creando en su proceso de diseño un nuevo desafío. En la Figura 1.9. se observa el proceso conocido como Epitaxia por haces moleculares que permite fabricar estructuras con precisión de unos pocos Angstroms (en un centímetro caben 10 millones de angstroms). Esta técnica es usada en el crecimiento de heteroestructuras de semiconductores por la gran perfección cristalina que alcanza. Los haces moleculares inciden sobre un sustrato y diversas reacciones químicas ocasionan la deposición de monocapas sucesivas. Mediante el adecuado control de las especies químicas de los haces se puede variar la composición de las capas epitaxiales. Los requerimientos técnicos son elevados pues se exige un perfecto control de la temperatura y vacío en la cámara de crecimiento.
| (a) | (b) |
| Figura 1.9. Epitaxia por haces moleculares. (a) Deposición de capas con absoluta precisión. (b) Cámara para crecimiento epitaxial. | |
Puesto que el sensor es un elemento fundamental en los sistemas de control, las nuevas tecnologías de desarrollo de sensores están proporcionando nuevas oportunidades en el desarrollo de controladores. Sensores con conexión directa al computador (controlador) de aplicación en láser backscattering9, vídeo microscopía, espectroscopía infrarroja y de Raman10, etc., están propiciando que procesos hasta ahora de laboratorio se estén incorporando al mundo industrial.
Robótica y máquinas inteligentes
El objetivo de la ingeniería cibernética, ya establecido en los años 40 e incluso antes, ha sido implementar sistemas capaces de exhibir respuestas muy flexibles o inteligentes ante cambios en la situación. De hecho, según la RAE, la cibernética estudia las analogías entre los sistemas de control y comunicación de los seres vivos y los de las máquinas; y en particular, el de las aplicaciones de los mecanismos de regulación biológica a la tecnología. Esto es, la cibernética está completamente ligada al control, y ambas disciplinas han sentado las bases de la robótica moderna.
Dos logros importantes en este ámbito son los Mars Exploratory Rovers y los robots de entretenimiento como el AIBO de Sony, los cuales se muestran en la Figura 1.10. Los Mars Exploratory Rovers han sido desarrollados por el Jet Propulsion Laboratory (JPL) y han estado maniobrando en la superficie de Marte durante más de 4 años, a partir de enero de 2004, enviando medidas y fotos de su entorno de trabajo. El robot AIB de Sony, lanzado al mercado en 1.999, fue el primer robot de entretenimiento lanzado en masa al mercado. Es digno de mencionar el uso que hacía de técnicas de inteligencia artificial que le permitían reaccionar ante estímulos según su propio juicio. Este altísimo nivel de realimentación es un elemento clave en robótica, donde cuestiones como el evitar obstáculos, seguir trayectorias, aprendizaje o autonomía son muy relevantes.
A pesar de los enormes progresos acontecidos en los últimos años en el campo de la robótica, en muchos aspectos está todavía en la infancia. Los robots de hoy en día exhiben comportamientos muy simples comparados con los humanos, y sus habilidades para moverse, interpretar señales externas complejas, realizar razonamientos de alto nivel y cooperar juntos en equipo son muy limitadas. Sin duda la combinación de técnicas de inteligencia artificial (planificación, adaptación y aprendizaje) con técnicas de control contribuirá a realizar mejoras continuas en los campos citados.
 |
 |
| (a) | (b) |
| Figura 1.10. Sistemas robóticos. (a) Spirit, uno de los dos robots exploradores de Marte que aterrizó en él en enero de 2004. (b) Robot AIBO de Sony, uno de los primeros robots de entretenimiento comercializados en masa. Aunque los dos sistemas robóticos tiene cometidos muy diferentes, ambos hacen uso de realimentación entre sensores, actuadores y de computación para funcionar en entornos desconocidos. | |
Redes y sistemas informáticos
El control de redes es una gran área de investigación que abarca muchos tópicos incluyendo el control de congestión de tráfico, enrutado, copiado de datos y gestión de energía. Varias características de estos problemas de control los hacen muy interesantes. La característica dominante en todos ellos es la enorme escala de los sistemas que han de ser controlados; Internet es probablemente el mayor sistema de control realimentado que la humanidad ha construido nunca. Otra característica es la naturaleza descentralizada del problema de control: las decisiones deben ser tomadas muy rápidamente y basándose sólo en información local. La estabilidad en Internet es muy complicada debido a los retardos de tiempo variable que se producen, con lo cual la información sobre la red puede ser observada o enviada a los controladores sólo después de un retardo, con lo cual la acción de control sobre la red se produce con un retraso considerable. Incertidumbres y variaciones en la red, cambios en su topología, características del canal de transmisión, demanda de tráfico y recursos disponibles están cambiando continuamente y en forma impredecible.
El control de las redes está también íntimamente relacionado con el control de los servidores que están conectados a ellas. Los computadores son los elementos claves de los routers, servidores web y servidores de bases de datos usados para comunicaciones, comercio electrónico, publicidad y almacenamiento de la información. Mientras que los costes de hardware (la electrónica) han disminuido de forma considerable, los de operación de estos sistemas han aumentado, debido a la dificultad en su gestión y mantenimiento, como consecuencia del grado de complejidad cada vez más acusado.
En la Figura 1.11 (a) se muestra un ejemplo de un sistema multicapas para e-comercio. El sistema tiene varias capas de servidores. La capa de cabecera acepta solicitudes entrantes y las enruta hacia la de servidores http, los cuales las distribuyen hacia los servidores de aplicaciones. El tratamiento de las solicitudes entrantes puede variar en un amplio rango, y los servidores de aplicaciones pueden acceder también a otros servidores externos gestionados por otras organizaciones.
El control de un servidor individual en una capa se muestra en la Figura 1.11 (b). Una cantidad que representa la calidad del servicio o el coste de la operación –tal como tiempo de respuesta, tasa de transferencia, servicio de atención al cliente o uso de memoria– se mide en el computador. Las variables de control pueden representar mensajes entrantes aceptados, prioridades en el sistema operativo o asignación de memoria. El lazo de realimentación ha de encargarse entonces de mantener las variables que representan la calidad del servicio dentro del rango de valores fijado.
| (a) | (b) |
| Figura 1.11. Ejemplo de sistema multicapas para servicios de Internet. (a) Los usuarios solicitan información desde un conjunto de computadores (capa 1), la cual a su vez recoge información de otros computadores (capas 2 y 3). (b) Cada servidor individual tiene un conjunto de parámetros de referencia fijados por el operador (humano) del sistema. La realimentación permite además operar al sistema en presencia de incertidumbres. | |
Economía
La economía es un sistema dinámico muy grande con muchos actores: gobiernos, organizaciones, compañías y particulares. Los gobiernos controlan la economía mediante leyes y tasas, los bancos centrales fijando el tipo de interés y las compañías estableciendo precios y realizando inversiones. Las personas particulares controlan la economía mediante compras, ahorros e inversiones. Se han realizado esfuerzos enormes para modelar el sistema tanto a nivel macro11 [13] como microeconómico12 [14] , pero el modelado es muy complicado, ya que el sistema está muy interrelacionado y, por tanto, muy influenciado por el comportamiento dentro de él de los diferentes actores.
J. M. Keynes desarrolló en 1936 un modelo simple para comprender relaciones entre producto nacional bruto, inversión, consumo y gasto público. Una de las observaciones de Keynes fue que bajo ciertas condiciones, por ejemplo durante la gran depresión de los años 30, un incremento en el gasto público podría llevar a un gran aumento en el producto nacional bruto. Esta idea fue usada por varios gobiernos con objeto de aliviar los efectos de la gran depresión. Las ideas de Keynes serán modeladas en el capítulo siguiente.
Una de las razones de porqué es muy difícil modelar sistemas económicos es que éstos no están sometidos a leyes de conservación. Un ejemplo típico es el valor en bolsa de una empresa, el cual puede cambiar rápida y erráticamente. No obstante lo anterior, sí hay áreas concretas con leyes de conservación que sí permiten elaborar modelos precisos. Un ejemplo es el flujo de productos desde un fabricante a un minorista tal como se ilustra en la Figura 1.12. Los productos son cantidades físicas que obedecen una ley de conservación, y el sistema puede ser modelado considerando las unidades de producto en los diferentes inventarios. El control de las cadenas de producción y consumo origina importantes beneficios económicos, ya que minimiza la cantidad de producto almacenado.
Los problemas reales son más complejos de lo que indica la Figura 1.11, ya que puede haber muchos productos diferentes, muchas fábricas distribuidas geográficamente y además éstas pueden requerir materias primas o productos semielaborados.
El control de las cadenas de producción y suministro fue propuesto por J. W. Forrester en 1961 y es hoy en día de gran importancia, ya que los beneficios económicos que se obtienen minimizando inventarios son considerables. Los modelos para reducir inventarios han sufrido un auge enorme gracias al uso de las tecnologías de la información y las comunicaciones, las cuales han permitido predecir ventas, seguir la pista de productos y ajustar en consecuencia la producción justo a tiempo13 [15]. Este control de las cadenas de producción y suministro ha proporcionado éxitos notables de distribuidores a nivel mundial (piénsese por ejemplo en las grandes cadenas de hipermercado, comida rápida, tiendas de moda franquiciadas, etc.) La publicidad en Internet es una aplicación emergente de control. Advertising on the Internet is an emerging application of control. La publicidad basada en redes permite medir los efectos de las diferentes estrategias de comercialización. Las respuestas de los consumidores pueden ser modeladas, lo cual permite elaborar estrategias de realimentación.
| Figura 1.12. Dinámica de la cadena de suministro. Los productos van desde el fabricante al cliente a través de distribuidores y detallistas tal como indican las líneas sólidas. Nótese los múltiples lazos de realimentación creados por las líneas discontinuas, los cales son originados porque cada agente trata de mantener su propio nivel de inventario. |
Industria farmacéutica
La industria farmacéutica ha tenido un desarrollo espectacular a partir de la mitad del siglo XX, cuando los medicamentos han comenzado ha llegar en masa a la población en general, y el acceso a ellos se ha convertido en algo rutinario para el ciudadano de los países desarrollados. Hoy en día la industria farmacéutica tiene ante sí grandes retos para resolver problemas de salud que azotan la humanidad: cáncer, sida, cardiopatías, etc. Por ello, las inversiones en desarrollo de medicamentos son enormes y, en consonancia, lo son también la complejidad de los laboratorios y las técnicas utilizadas. Un ejemplo de esto puede ser la industria biofarmacéutica, y dentro de ella la producción industrial de anticuerpos monoclonales14 [16] (MAB), debido a sus aplicaciones tanto diagnósticas como clínicas. Este es un campo que se encuentra actualmente en pleno desafío investigador y tecnológico.
Concretando aún más en el ejemplo, hay un gran número de complicaciones que dificultan la producción industrial de la célula hybridoma15, por ello el control industrial actual del cultivo de esta célula se realiza de forma manual. Las complicaciones que surgen para realizar un control automático radican en los requerimientos tan estrictos que exigen el crecimiento de los cultivos, la ausencia de medidas en línea de substratos esenciales en el proceso, la escasez de datos experimentales precisos, así como la dinámica extremadamente compleja del proceso. Con objeto de considerar todas las variables del proceso y la interacción entre ellas, a escala industrial se tiende a integrar el modelado, el diseño del experimento y la validación, el control y la optimización en un mismo sistema (ver Figura 1.13) que permita incrementar la productividad, regular la calidad del producto y reducir costes.
| Figura 1.13. |
Realimentación en la naturaleza
El desarrollo de metodologías rigurosas que permitan modelar el comportamiento de sistemas naturales complejos (debido a la interacción de multitud de sistemas, la mayoría de las veces muy simples, pero con intrincados patrones de flujo de información) es un aspecto de la dinámica de sistemas16 [17]. Los avances que se están produciendo en ciencia y tecnología están permitiendo concebir una comprensión más amplia en el comportamiento (dinámica) de sistemas complejos que se dan en la naturaleza. Por poner sólo algunos ejemplos:
Sistemas biológicos. Hay un interés enorme en conocer de forma fehaciente los mecanismos que se dan a nivel celular (ver en la Figura 1.14 el caso particular de las metaloproteínas17 [18]), no sólo por el hecho de utilizar este conocimiento a nivel médico para curar enfermedades, sino, como vimos en el apartado anterior, para producir medicamentos, sustancias, células, etc., a nivel industrial. Hay una gran variedad de fenómenos biológicos que proporcionan una fuente amplia de ejemplos de control, incluyendo regulación genética, mecanismos de realimentación hormonal, inmunológica y cardiovascular, control muscular y locomotor; percepción activa, visión y recepción de información sobre la localización del cuerpo, sus movimientos y el sistema sensitivo; atención y conciencia; dinámica de poblaciones y epidemias. Cada una de ellas (y muchas otras más) proporcionan oportunidades para explicar lo que funciona, cómo funciona y qué podemos hacer para afectar su funcionamiento.
| Figura 1.14. Caminos del tráfico de cobre en la célula de un mamífero. Este conocimiento es fundamental para fabricar metaloproteínas. |
Ecosistemas. Un ecosistema es un sistema natural que está formado por un conjunto de organismos vivos (biocenosis) y el medio físico en donde se relacionan (biotopo). Un ecosistema es una unidad compuesta de organismos interdependientes que comparten el mismo hábitat (ver Figura 1.15). Los ecosistemas suelen formar una serie de cadenas que muestran la interdependencia de los organismos dentro del sistema. Los ecosistemas son sistemas dinámicos complejos de múltiples escalas, que proporcionan una nueva y amplia gama de desafíos para el modelado y análisis de sistemas realimentados. La experiencia reciente en la aplicación de técnicas de control y modelado de sistemas dinámicos a las redes de bacterias, sugiere que gran parte de la complejidad de estas redes se debe a la presencia de múltiples capas de lazos de realimentación que proporcionan una funcionalidad robusta a la celda individual. Sin embargo, en otros casos, los acontecimientos a nivel celular benefician a la colonia a expensas del individuo. Análisis a nivel de sistemas se pueden aplicar a los ecosistemas con el objetivo de comprender la solidez de esos sistemas, y la medida en que las decisiones y acontecimientos que afectan a las especies individuales contribuyen a la solidez y/o fragilidad del ecosistema en su conjunto.
| (a) | (b) |
| Figura 1.15. Ejemplo de ecosistemas. (a) Sabana (Tanzania). (b) Arrecife de coral en la Gran Barrera de Coral, el mayor arrecife de coral del mundo, situado en el Mar del Coral, frente a la costa de Queensland al noreste de Australia. | |
Ciencias ambientales. Las Ciencias Ambientales son un área de la ciencia cuyo objetivo principal es buscar y conocer las relaciones que mantiene el ser humano consigo mismo y con la naturaleza. Ya se sabe que las actividades humanas han alterado el medio ambiente a escala mundial. Los investigadores en este ámbito se enfrentan a problemas de enorme complejidad; quizás el primero de ellos es comprender los sistemas de retroalimentación que operan a escala mundial..
Las ciencias ambientales Implican un área de estudio multidisciplinar que abarca distintos elementos. Incluye el estudio de problemas ambientales y la propuesta de modelos para el desarrollo sostenible. Así por ejemplo, las ciencias ambientales estudian la depuración y el tratamiento de aguas (ver Figura 1.16 (a)); esto es, el conjunto de operaciones unitarias de tipo físico, químico o biológico cuya finalidad es la eliminación o reducción de la contaminación o las características no deseables de las aguas, bien sean naturales, de abastecimiento, de proceso o residuales —llamadas, en el caso de las urbanas, aguas negras—. La finalidad de estas operaciones es obtener unas aguas con las características adecuadas al uso que se les vaya a dar, por lo que la combinación y naturaleza exacta de los procesos varía en función tanto de las propiedades de las aguas de partida como de su destino final. Otro ejemplo del campo de las ciencias ambientales es la gestión de residuos. Los residuos no aprovechables constituyen un problema para muchas sociedades, sobre todo para las grandes urbes, así como para el conjunto de la población del planeta, debido a que la sobrepoblación, las actividades humanas modernas y el consumismo, han acrecentado mucho la cantidad de basura que se genera (ver Figura 1.16 (b)); lo anterior junto con el ineficiente manejo que se hace con dichos residuos (quemas a cielo abierto, disposición en tiraderos o vertederos ineficientes), provoca problemas tales como la contaminación, que origina problemas de salud y daño al ambiente, además deprovocar conflictos sociales y políticos.
| (a) | (b) |
| Figura 1.16. Ejemplo de campos de trabajo de las ciencias ambientales. (a) Planta de depuración y tratamiento de aguas. (b) Desechos sólidos caseros clasificados. 1) envases de vidrio, 2) plástico fino, 3) plástico grueso, 4) cartón, 5) varios, 6) latas compactadas, 7) papel, 8) poliestireno, 9) pedacería de vidrio, 10) pilas, 11) metales diversos, 12) orgánicos, 13) tetrapak, 14) telas, 15) sanitarios. | |
La realimentación es una idea o concepto que, tal como se ha visto, es de uso muy extendido en la naturaleza. ¿Por qué es tan importante la realimentación? Pues porque como veremos a continuación de forma intuitiva (la formalización de estas intuiciones se realizará en capítulos sucesivos), dota a los sistemas de unas propiedades que mejoran su funcionamiento de forma notable. El principio de la realimentación es simple: la corrección de las acciones sobre la base de la diferencia entre el rendimiento real y el deseado. En ingeniería, la realimentación ha sido redescubierta y patentada muchas veces en muchos contextos diferentes.
Robustez frente a la incertidumbre
Uno de los usos fundamentales de la realimentación es hacer al sistema robusto frente a la incertidumbre. Calculando la diferencia entre el valor medido de una señal regulada y su valor deseado, se obtiene una señal de error que puede ser usada para suministrar una acción correctiva al sistema con objeto de llevar el error a cero. Este es precisamente el concepto que explotó Watt cuando diseñó el regulador de bolas (ver sección 1.2) para regular la velocidad en las máquinas de vapor. Como un ejemplo más moderno considérese el sistema de la Figura 1.17. En él, la velocidad del vehículo se controla mediante el acelerador o el freno. Para ello el sistema de control mide la velocidad del vehículo, la cual compara el controlador (computador) con la velocidad prefijada por el conductor. Si ésta es mayor que la deseada, el sistema de control acciona el freno, y si es menor el acelerador. El gráfico de la derecha muestra que ante un cambio en la velocidad prefijada, el sistema es muy robusto frente a la incertidumbre en la masa de la planta (un número diferente de pasajeros por ejemplo), ya que a pesar de un aumento de ésta, el sistema sigue estabilizando la velocidad prefijada en aproximadamente 5 s.
| Figura 1.17. Sistema para el control de la velocidad de un vehículo. En la Figura de la izquierda se muestra el diagrama de bloques del sistema. En la Figura de la derecha se muestra la respuesta del control de velocidad ante un cambio de 25 a 30 m/s en la velocidad de consigna o deseada por el conductor. |
Otro ejemplo temprano del uso de la realimentación para proporcionar robustez en un sistema es el amplificador con realimentación negativa. El concepto de realimentación, como ya se sabe a estas alturas del texto, consiste en combinar una fracción de la salida de un sistema con su entrada. Si la fracción de señal realimentada se opone a la señal de entrada, la realimentación se denomina negativa, y si se suma a la señal de entrada se denomina positiva. Un amplificador con realimentación negativa, o más comúnmente denominado amplificador realimentado, es un amplificador que emplea realimentación negativa para mejorar sus prestaciones (estabilidad en su ganancia, linealidad, respuesta en frecuencia, respuesta a cambios en su entrada) y su robustez a las incertidumbres (variaciones en sus parámetros internos —debido a tolerancias en la fabricación o deterioros de los componentes— o externos —condiciones ambientales por ejemplo). En la Figura 1.18 se muestra el diagrama de bloques más simple de un amplificador realimentado, donde AOL es la ganancia del amplificador en lazo abierto, y la fracción (β.Salida) se realimenta a la entrada con signo menos.
El amplificador realimentado fue inventado por Harold Stephen Black (Patente americana 2.102.671 (publicada en 1937)). Black solicitó la patente en 1928, y le costó más de 9 años que fuera publicada. Black escribió más tarde: Una de las razones de la demora fue que el concepto era tan contrario a las creencias establecidas que inicialmente la Oficina de Patentes no creyó que funcionaría.
| Figura 1.18. Esquema básico de un amplificador realimentado |
Cambios en la dinámica de un sistema
Otro efecto de la realimentación es que permite cambiar la dinámica de un sistema. Esto es, su comportamiento puede ser cambiado en función de los requerimientos de una aplicación determinada: sistemas inestables pueden ser estabilizados, sistemas poco sensibles ante excitaciones pueden ser sensibilizados y sistemas con puntos de operación erráticos pueden ser mantenidos constantes. La teoría de control proporciona una colección muy rica de técnicas para analizar la estabilidad y respuesta dinámica de sistemas muy complejos, y para determinar el comportamiento de tales sistemas tanto para el caso de que puedan ser considerados lineales como no lineales.
Un ejemplo claro de cómo el control puede transformar la dinámica de un sistema se encuentra en el control del vuelo de aeronaves. Las palabras siguientes, extraídas de una conferencia impartida por Wilbur Wright en 1901, en la Western Society of Engineers, ilustra la importancia del control en el desarrollo del aeroplano.
Los hombres ya saben cómo construir alas o aviones, que cuando se impulsan por el aire a una velocidad suficiente, no sólo mantienen el peso de las alas mismas, sino también el del motor y el ingeniero. Los hombres saben también cómo construir motores y tornillos de la ligereza y potencia suficientes para llevar esos aviones a la velocidad de sustentación... La incapacidad para estabilizar y dirigir aún enfrenta a los estudiosos del problema de volar... Cuando este aspecto haya sido resuelto, la era de volar habrá llegado, dado que el resto de problemas son de menor importancia.
Los hermanos Wright se dieron cuenta enseguida que resolver el problema del control del aeroplano era un asunto clave para conseguir volar. Ellos resolvieron el compromiso entre la estabilidad y la maniobrabilidad construyendo un aeroplano, el Wright Flyer, que era inestable pero manejable. El Flyer tenía un timón en la parte delantera del avión, lo cual lo hacía muy manejable. Una desventaja era que el piloto debía estar continuamente manteniendo el timón, ya que si lo dejaba suelto el avión se estrellaba. Otros pioneros de la aviación trataron de construir aviones estables. Estos podrían haber tenido más fácil volar, sin embargo su escasa maniobrabilidad no les permitía ser conducidos por el aire. Como ya se ha indicado en este texto (ver sección 1.2), el compromiso estabilidad – maniobrabilidad que permitió hacer volar un avión por primera vez lo resolvieron los hermanos Wright en 1903.
El enorme esfuerzo que suponía para el piloto mantener estable aquellos primeros aeroplanos, generó bastante empeño en encontrar un sistema que los estabilizara de forma más o menos automática. Así, en 1912 la compañía norteamericana Sperry, basándose en el concepto de realimentación, desarrolló el primer piloto automático (Sperry autopilot). Lawrence Sperry (hijo del famoso inventor Elmer Sperry18 [19]) lo mostró dos años más tarde, en 1914, y demostró la credibilidad de su invento haciendo volar el avión mientras mantenía sus manos en alto [20]19. El piloto automático conectaba un indicador de altitud giroscópico [21]20 y una brújula magnética a un timón, elevador y alerones operados hidráulicamente. Esto permitía que el avión volase recto y nivelado respecto a una dirección de la brújula sin la atención del piloto, cubriendo así más del 80% del trabajo total de un piloto en un vuelo típico. Este piloto automático que permite seguir recto y nivelado sigue siendo el tipo más común, menos caro y más confiable. También tiene el menor error de pilotaje, al tener los controles más simples. El piloto automático es un ejemplo excelente de cómo la realimentación puede ser usada para estabilizar un sistema inestable y, consecuentemente, modificar la dinámica del avión.
Niveles más elevados de automatización
Hoy en día, el concepto de control, gracias al concurso de otras técnicas pertenecientes a otras ramas de la ciencia, fundamentalmente la inteligencia artificial, ha dado un salto cualitativo y cuantitativo que le ha permitido adentrarse en la optimización (control óptimo), adaptación (control adaptativo), aprendizaje y razonamiento (control inteligente).
Una de las áreas de investigación del control en los niveles más altos de decisión es el control autónomo de vehículos. En este campo se están realizando innumerables aportaciones, muchas de las cuales están ya en el mercado, como por ejemplo el Control de Velocidad de Crucero Adaptativo (ACC) que adapta automáticamente la velocidad del vehículo a las condiciones del tráfico.
Prueba del interés en el control autónomo de vehículos es el Darpa Grand Challenge, una carrera de vehículos autónomos21 [22] que deben llegar desde un punto de los Estados Unidos hasta otro sin intervención humana, sólo disponiendo de un listado de puntos intermedios entre el principio del circuito y el final. La primera edición se celebró en 2004 en el desierto del Mojave y ningún vehículo consiguió terminar. En 2005 varios vehículos lograron terminar el circuito, siendo el equipo de la Universidad de Stanford el ganador. La siguiente edición, conocida como 2007 Urban Challenge, introdujo una dificultad adicional, ya que se celebró en un circuito urbano donde los participantes debían obedecer las normas de tráfico y comportarse responsablemente. El ganador fue el equipo Tartan Racing de la Universidad de Pittsburgh, Pensilvania (2.000.000 $ de premio), seguido del equipo Stanford Racing de la Universidad de Stanford, California (1.000.000 $ de premio). En la Figura 1.19 se observan detalles de la carrera.
| Figura 1.19. Fotografías de la 2007 Urban Challenge. Superior izquierda: El equipo ganador de la Universidad de Pittsburgh. Superior derecha: el equipo que quedó en segundo lugar de la Universidad de Stanford. Inferior izquierda: El equipo Victor Tango de la Universidad de Blacksburg, Virginia, que quedó en tercer lugar, circulando entre 4 vehículos conducidos por personas. Inferior derecha: Los equipos de Pittsburgh y Standford juntos, en una intersección. |
Desventajas de la realimentación
Aunque la realimentación tiene muchas ventajas, también tiene algunas, aunque pocas, desventajas. La principal quizás sea que si el sistema no está bien diseñado se puede originar inestabilidad. Un ejemplo muy familiar de esto es cuando el exceso de amplificación de un micrófono, como consecuencia de la realimentación positiva, produce sonidos estridentes en una habitación. Lo anterior indica que un sistema ha de ser diseñado para que sea estable no sólo bajo condiciones nominales, sino también bajo todas las posibles perturbaciones que sufra su dinámica.
Otro problema común debido a la realimentación es el posible ruido de medida que se introduce en el sistema, de ahí que la señal medida deba ser filtrada adecuadamente, con objeto de que su posible ruido no se incorpore a la dinámica del proceso (ver Figura 1.1).
Control por anticipación (Feedforward)
El control por realimentación del error es reactivo: para que se tome una acción correctiva ha de entrar antes un error al sistema. Piénsese en un sistema de control como el de la Figura 1.17 por ejemplo. En él, se ha de seguir una señal de referencia (velocidad) fijada por el conductor. Cada vez que la referencia cambia, el sistema de control no comienza a actuar hasta que no se detecta un error entre la señal de referencia fijada y la velocidad real del vehículo. Cuanto más rápido cambie la señal de referencia menos efectiva se mostrará la acción de control, ya que parecerá que va por detrás. Lo anterior sugiere que cuando la señal de referencia cambia rápidamente, el seguimiento a tiempo puede lograrse si se tiene disponible y se utiliza una información anticipada de la referencia, tal como la velocidad de cambio (derivada) y la velocidad de cambio de segundo orden (derivada segunda o curvatura). Esta información está con frecuencia disponible en aplicaciones donde la trayectoria de referencia se planifica y almacena en la memoria del controlador (computador). A partir de aquí, el sistema de control se puede adelantar y tomar alguna acción correctiva antes de que el cambio en la referencia a seguir genere un error en la salida. Evidentemente, en el momento del cambio siempre se generará un error, por pequeño que sea, lo que ocurre es que el sistema de control lo anulará mucho más rápidamente. Esta forma de control se denomina por anticipación, en inglés feedforward.
Las ideas de control por realimentación y control por anticipación son muy generales y aparecen en campos muy diversos. En economía, un control por realimentación puede ser asociado a una economía basada en la respuesta del mercado, y un control por anticipación a una economía basada en planificación. En biología, una estrategia de control por anticipación es un principio fundamental en el control del movimiento de las personas y animales, el cual, durante la infancia, es ajustado mediante entrenamiento. En general, la mayor efectividad de control se logra cuando realimentación y anticipación (no siempre es posible) se aplican de forma conjunta.
1.1 Prepare, si no lo domina, el capítulo 1 del manual docente: Andújar J. M., et al. Guía práctica de simuladores de circuitos y sistemas electrónicos II. Servicio de Publicaciones de la Universidad de Huelva, ISBN 84-95699-16-8, 2001. Realice todos los ejercicios resueltos, ya que MATLAB será una herramienta de uso constante en la signatura.
1.2 Prepare, si no lo domina, el capítulo 2 del manual docente: Andújar J. M., et al. Guía práctica de simuladores de circuitos y sistemas electrónicos II. Servicio de Publicaciones de la Universidad de Huelva, ISBN 84-95699-16-8, 2001. Es importante que se familiarice con las posibilidades de SIMULINK (la versión más moderna que seguro utilizará respecto de la explicada en el texto ofrecerá muchas más prestaciones), ya que será una herramienta de uso continuo en la asignatura.
1.3 Busca en Internet una animación de la suspensión cardan y explica sus funcionamiento. A partir de aquí intenta razonar el funcionamiento del giróscopo.
1.4 Identifique 5 sistemas de control presentes en su entorno diario. Para cada uno de los sistemas identifique los mecanismos que hacen el sensado y la actuación, así como la ley de control. Identifique también respecto de qué incertidumbres proporciona robustez el sistema de control y/o la modificación de la dinámica del sistema que se consigue con la realimentación.
1.5 Manténgase en equilibrio sobre un pie con los ojos cerrados durante 15 segundos. Usando la Figura 1.1 como guía, describa el sistema de control responsable de que no se caiga. Por supuesto, la arquitectura del controlador tendrá otra concepción en este caso respecto de la presentada en la Figura 1.1.
1.6 Realice una búsqueda en la red y localice un artículo de prensa divulgativa sobre algún sistema de control. Describa, a partir de la terminología usada en el artículo, el sistema. De forma específica identifique el sistema de control y describa: (a) la planta controlada, junto con el (b) sensor, (c) actuador y (d) elementos de computación. Si alguna información no estuviera disponible en el artículo, coméntelo y proponga, según su opinión, qué podría usarse.
Al igual que hace el Control de Velocidad de Crucero, el Control de Velocidad de Crucero Adaptativo (ACC) también regula la velocidad a la que deseamos circular de forma automática. La novedad reside en que además, con la ayuda de un sistema de radar controla, también de forma automática, la distancia de circulación con respecto al vehículo precedente, frenando nuestro vehículo si es necesario para mantener dicha distancia de seguridad. Una vez que el carril por el que circulamos queda libre, el ACC acelera el vehículo hasta la velocidad que hayamos programado.
El control de tracción (EDS del inglés Electronic Differential System) busca la mejor motricidad del vehículo para evitar el patinado de los neumáticos sobre firme deslizante o bajo una fuerte aceleración. Su función es conseguir que las ruedas motrices se muevan a la misma velocidad. Para ello utiliza la instalación de freno y aprovecha el sistema ABS para su funcionamiento.
El control de estabilidad (ESP del alemán Elektronisches Stabilitätsprogramm) mejora el EDS en el sentido que éste sólo evita que se produzcan pérdidas de motricidad por exceso de aceleración, y no es capaz de recuperar la trayectoria del vehículo en caso de excesivo subviraje o sobreviraje, lo cual sí consigue el ESP. Este sistema fue desarrollado originalmente por Mercedes-Benz y Bosch, y hoy en día lo desarrollan y comercializan otros fabricantes con nombres como Vehicle Dynamic Control (VDC), Dynamic Stability Control (DSC), Electronic Stability Control (ESC) y Vehicle Stability Control (VSC).
Alas pequeñas (fijas o movibles) que son colocadas antes de las alas principales del avión. En inglés se denominan canards
Fly-by-wire, traducido literalmente del inglés como vuelo por cable, es un sistema de control de las superficies de sustentación o de dirección de un avión, que se basa en el uso de servomotores que, mediante impulsos eléctricos activados por computadora, desplazan fluido hidráulico hasta aquellas. Es este último el que finalmente termina realizando los efectivos movimientos y ajustes necesarios en tiempo real. De esa manera indirecta se mueven las diferentes superficies de vuelo, como son el timón de dirección, el de profundidad (elevator), los alerones, los flaps (situados en el borde de fuga de las alas permiten mediante su giro aumentar la superficie de sustentación), los slats (situados en el ángulo de ataque de las alas permiten modificar éste) o el freno aerodinámico. Los controles fly-by-wire fueron incorporados en aviones militares estadounidenses ya en la década de 1970, como sucedió en los casos del F-16 Fighting Falcon, el F/A-18 Hornet y el F-15 Eagle. Por su parte, el francés Mirage 2000, lanzado en 1978, también los incluye.
La Heliopausa es el punto en el que el viento solar se une al medio interestelar o al viento estelar procedente de otras estrellas. Es un límite teórico aproximadamente circular o en forma de lágrima, que señala el límite de influencia del Sol. Se localiza en el punto en el que la pérdida de presión del viento solar causada por la dispersión inherente a su difusión radial iguala a la presión exterior del medio interestelar. La Heliopausa señala la frontera entre el Sistema Solar y el espacio interestelar.
El control en la industria química suele denominarse con el nombre genérico de control de procesos.
Se trata en pocas palabras de aprovechar el calor generado en un proceso químico para producir también electricidad. Al generar electricidad mediante un alternador, movido por un motor térmico o una turbina, el aprovechamiento de la energía química del combustible es del 25% al 40% solamente, y el resto debe disiparse en forma de calor. Con la cogeneración se aprovecha una parte importante de la energía térmica que normalmente se disiparía a la atmósfera o a una masa de agua y evita volver a generarla con una caldera.
Backscatter o backscattering es la reflexión de ondas, partículas, o señales en sentido opuesto al de avance.
La espectroscopia Raman (llamada así por C.V. Raman) es una técnica espectroscópica usada en química y física de la materia condensada para estudiar modos de baja frecuencia como los vibratorios, rotatorios, y otros. El efecto de Raman se produce cuando la luz choca sobre una molécula e interacciona con la nube de electrones de los enlaces de esa molécula.
La macroeconomía es la parte de la economía encargada del estudio global de la economía en términos del monto total de bienes y servicios producidos, el total de los ingresos, el nivel de empleo, de recursos productivos, y el comportamiento general de los precios. La macroeconomía puede ser utilizada para analizar cuál es la mejor manera de influir en objetivos políticos como por ejemplo hacer crecer la economía, estabilidad de precios, trabajo y la obtención de una sustentable balanza de pagos.
La microeconomía es una parte de la economía que estudia el comportamiento económico de agentes individuales, como son los consumidores, las empresas, los trabajadores e inversores; así como de los mercados. Considera las decisiones que toma cada uno para cumplir ciertos objetivos propios. La microeconomía tiene varias ramas de desarrollo, las más importantes son: la teoría del consumidor, la de la demanda, la del productor, la del equilibrio general, y la de los mercados de activos financieros. No pueden considerarse enteramente separadas porque los resultados de unos aspectos influyen sobre los otros. Por ejemplo, las empresas no sólo ofertan bienes y servicios, sino que también demandan bienes y servicios para poder producir los suyos.
El término justo a tiempo es una traducción de la expresión inglesa just-in-time, la cual da nombre a un sistema de organización de la producción para las fábricas denominado método Toyota o JiT. Las compañías japonesas que durante los últimos años han adoptado este método han aumentado su productividad en los últimos 20 años.
Un anticuerpo monoclonal es un anticuerpo homogéneo producido por una célula híbrida producto de la fusión de un clon de linfocitos B, descendiente de una sola y única célula madre y una célula plasmática tumoral. Los anticuerpos monoclonales (MAB, del inglés monoclonal antibody), son anticuerpos idénticos porque son producidos por un solo tipo de célula del sistema inmune, es decir, todos los clones proceden de una sola célula madre. Es posible producir anticuerpos monoclonales que se unan específicamente con cualquier molécula con carácter antigénico (un antígeno es una sustancia que, introducida en un organismo animal, da lugar a reacciones de defensa, tales como la formación de anticuerpos). Este fenómeno es de gran utilidad en bioquímica, biología molecular y medicina.
Las células hybridoma son células que han sido diseñadas para producir un anticuerpo concreto en grandes cantidades. Éstas células, al ser cancerígenas, se multiplican rápida e indefinidamente, produciendo enormes cantidades del anticuerpo deseado.
La dinámica de sistemas es una metodología considerada por muchos autores como parte de la automática. Está dedicada a la construcción de modelos de simulación para sistemas complejos como los estudiados por las ciencias sociales, la economía o la ecología. Quizás, la principal característica de estos modelos es que sus elementos están relacionados formando lazos de realimentación.
En bioquímica, una metaloproteina es un término genérico que alude a una proteína que contiene un metal como componente químico.
Prolífico inventor y hombre de negocios norteamericano, autor de más de 400 patentes. Nació en 1860 en Cortland, Nueva York, y murió en 1930 en Brooklyn, Nueva York. Sperry diseñó un girocompás (patentado en 1908), instalado por primera vez en el acorazado norteamericano Delaware en 1911, que permite pilotar de forma automática y fiable aviones, barcos y hasta naves espaciales.
Esto lo hizo en el Concours de la Securité en Aéroplane (concurso de la seguridad en aeroplano) que se celebró en las orillas del río Sena el 18 de junio de 1914.
El giroscopio fue inventado en 1852 por Léon Foucault, quien también le dio el nombre, montando una masa rotatoria en un soporte de Cardano (el soporte denominado Cardán, del francés cardan, por alusión a su inventor, el italiano Girolamo Cardano, 1501-1576, es un mecanismo de suspensión, consistente en dos círculos concéntricos cuyos ejes forman ángulo recto, que permite mantener la orientación de un eje de rotación en el espacio aunque su soporte se mueva) para un experimento de demostración de la rotación de la tierra. La rotación ya había sido demostrada con el péndulo de Foucault. Sin embargo, Foucault no comprendía el por qué la velocidad de rotación del péndulo era más lenta que la velocidad de rotación de la tierra por un factor sen λ, donde λ representa la latitud en que se localiza el péndulo. Se necesitaba otro aparato para demostrar la rotación de la tierra de forma más simple. Foucault presentó así un aparato capaz de conservar una rotación suficientemente rápida (150 a 200 vueltas por minuto) durante un tiempo suficiente (una decena de minutos) para que se pudiesen hacer medidas. Esta proeza mecánica (para la época) ilustra el talento de Foucault y su colaborador Froment en mecánica. Foucault también se dio cuenta de que su aparato podía servir para indicar el Norte. En efecto, si se impiden ciertos movimientos del soporte del giroscopio, este se alinea con el meridiano. Esto permitió la invención del girocompás.
Un vehículo autónomo terrestre es un vehículo que navega y se conduce por sí mismo sin intervención humana, ni siquiera por control remoto. Mediante el uso de sensores y sistemas de posicionamiento, el vehículo determina todas las características requeridas de su entorno así como las acciones a realizar para poder cumplir la tarea que se le ha asignado.
Modelado
Desde el punto de vista de la Automática, el modelo es la representación matemática de la planta a controlar, el cual permite analizar, describir, explicar y simular su comportamiento dinámico. Tanto por la descripción matemática utilizada como por la precisión considerada, una misma planta puede tener muchos modelos diferentes, todos igualmente válidos en su rango de consideración. En este capítulo se realizará una introducción al modelado de sistemas dinámicos (modelo dinámico) haciendo hincapié en las dos representaciones matemáticas de mayor interés en automática: modelado en ecuaciones diferenciales, de aplicación a los sistemas de tiempo continuo, y modelado en ecuaciones en diferencias, de aplicación a los sistemas discretos. A partir de estas dos representaciones se obtendrán los modelos de estado continuo y discreto, respectivamente, así como sus representaciones en forma de función de transferencia. Éstas últimas sólo aplicables a sistemas lineales y de una entrada – una salida.
En este capítulo, igual que en el resto del libro, se supondrá que el lector está familiarizado con MATLAB, no obstante, cuando se crea oportuno, se hará referencia a funciones específicas de MATLAB (en este tipo de letra) que resuelven operaciones concretas. Tecleando desde MATLAB el comando help seguido del nombre de la función, se obtiene en línea la informa-ción necesaria sobre la sintaxis y posibilidades de la función invocada.
La respuesta de un sistema dinámico a una acción sobre él no ocurre de forma inmediata. El dolor en el cuerpo no desaparece de forma inmediata al tomar un analgésico, sino que la respuesta lleva un tiempo. Tampoco sube de forma inmediata la temperatura en una habitación al encender la calefacción. En general la respuesta de un sistema dinámico a un estímulo lleva un tiempo, el cual depende de la naturaleza del estímulo y de la del sistema. El comportamiento temporal de un sistema ha de quedar reflejado en su modelo dinámico, el cual suele nacer a partir de la aplicación sobre él del conocimiento apropiado al sistema en cuestión: físico, económico, médico, etc.
Ejemplo 2.1. Sistema mecánico. Sea por ejemplo el sistema de la Figura 2.1 que representa un sistema muelle – masa – resorte, sujeto a sendos puntos fijos por ambos extremos. La variable 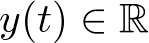 representa la posición de la masa m respecto de su posición de equilibrio
representa la posición de la masa m respecto de su posición de equilibrio 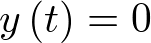 . Aplicando la segunda ley de Newton al sistema:
. Aplicando la segunda ley de Newton al sistema:
 |
(2.1) |
Esto es,
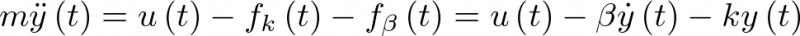 |
(2.2) |
Donde ![\[\ddot y\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.1-3_0.png) representa, según la notación usual en mecánica, la derivada segunda de
representa, según la notación usual en mecánica, la derivada segunda de 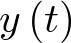 respecto del tiempo (aceleración de la masa;
respecto del tiempo (aceleración de la masa; 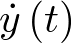 sería la derivada primera, esto es, su velocidad);
sería la derivada primera, esto es, su velocidad); 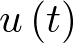 es la fuerza externa aplicada (entrada al sistema);
es la fuerza externa aplicada (entrada al sistema); ![\[{f_k}\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.1-7.png) es la fuerza de reacción del muelle, la cual, si se asume por simplificar que el muelle cumple la ley de Hooke, está dada por
es la fuerza de reacción del muelle, la cual, si se asume por simplificar que el muelle cumple la ley de Hooke, está dada por 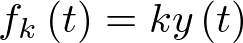 . Por último, asumiendo también que el elemento de fricción (amortiguador) se comporta linealmente, su oposición al desplazamiento es proporcional a la velocidad del movimiento,
. Por último, asumiendo también que el elemento de fricción (amortiguador) se comporta linealmente, su oposición al desplazamiento es proporcional a la velocidad del movimiento, ![\[{f_\beta }\left( t \right) = \beta \dot y\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.1-9.png) .
.
|
|
| Figura 2.1. Sistema muelle – masa – amortiguador. |
El sistema de la Figura 2.1 se dice que es de segundo orden porque su dinámica depende de las dos primeras derivadas de 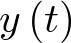 . La ecuación diferencial (2.2) se denomina forzada o controlada porque el sistema está forzado o controlado por la entrada
. La ecuación diferencial (2.2) se denomina forzada o controlada porque el sistema está forzado o controlado por la entrada 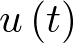 . Si no hubiera influencia externa en el sistema (la ecuación estaría igualada a cero,
. Si no hubiera influencia externa en el sistema (la ecuación estaría igualada a cero,  ), éste (su ecuación) se denominaría no forzado o autónomo. Desde la perspectiva acción – reacción, la entrada del sistema es la fuerza aplicada
), éste (su ecuación) se denominaría no forzado o autónomo. Desde la perspectiva acción – reacción, la entrada del sistema es la fuerza aplicada 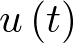 y la salida el desplazamiento o respuesta
y la salida el desplazamiento o respuesta 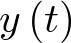 . El sistema de la Figura 2.1 es lineal1 [23] debido a las simplificaciones realizadas (ni el muelle ni el amortiguador lo son realmente) y, además invariante con el tiempo (la respuesta ante una misma excitación es la misma para todo tiempo t), aunque realmente no es así. Por ejemplo, el comportamiento del muelle dependerá de la temperatura de su entorno. Lo mismo sucederá con el comportamiento del fluido que contenga el amortiguador. No obstante lo anterior, la mayoría de los sistemas, dentro de ciertas condiciones de funcionamiento, pueden ser considerados lineales e invariantes con el tiempo o, de manera abreviada LTI (del inglés Linear Time-Invariant).
. El sistema de la Figura 2.1 es lineal1 [23] debido a las simplificaciones realizadas (ni el muelle ni el amortiguador lo son realmente) y, además invariante con el tiempo (la respuesta ante una misma excitación es la misma para todo tiempo t), aunque realmente no es así. Por ejemplo, el comportamiento del muelle dependerá de la temperatura de su entorno. Lo mismo sucederá con el comportamiento del fluido que contenga el amortiguador. No obstante lo anterior, la mayoría de los sistemas, dentro de ciertas condiciones de funcionamiento, pueden ser considerados lineales e invariantes con el tiempo o, de manera abreviada LTI (del inglés Linear Time-Invariant).
Cuando en 1683 Isaac Newton, para muchos el científico más grande que ha dado la historia2 [24], publicó los Philosophiae [25] Naturalis Principia Mathematica3 [25], el Cielo y la Tierra quedaron finalmente unificados en la Física, ya que demostró que las leyes naturales que gobiernan el movimiento en la Tierra y las que gobiernan el movimiento de los cuerpos celestes son las mismas4 [26]. Newton observó que el movimiento de los planetas podía ser predicho únicamente a partir de sus posiciones actuales y de sus velocidades. Esto es, no era necesario saber nada del movimiento pasado hasta el instante actual. Consecuentemente había definido el concepto de estado de un sistema dinámico (en este caso el sistema planetario) como el conjunto mínimo de variables (que denominaremos variables de estado) que permite determinar completamente su movimiento futuro. Este concepto será formalizado y generalizado en la sección siguiente.
El concepto de modelo de estado implica la representación del comportamiento dinámico de un sistema en base a un conjunto de ecuaciones diferenciales ordinarias (EDO) de primer orden, caracterizadas por la expresión siguiente:
![\[\frac{{d{\bf{x}}\left( t \right)}}{{dt}} = {\bf{f}}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right)} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\]](/antonio.barragan/files/archivos_usuarios/78/form2.1-13%282.3%29.png) |
(2.3) |
Esta ecuación vectorial se denomina ecuación de estado. En ella 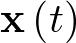 es el vector estado y sus coordenadas son las variables de estado (en el sistema mecánico de la Figura 2.1 sería un vector de 2 coordenadas: posición y velocidad). La variación del vector de estado respecto al tiempo se representa como una función vectorial, generalmente no lineal, cuyo argumento son los vectores de estado y de entrada5 [27]. El conjunto de todos los estados que puede alcanzar un sistema se denomina su espacio de estado. Puesto que cada estado estará caracterizado por un valor concreto de las variables de estado, el espacio de estado tiene por ejes coordenados las variables de estado. Así por ejemplo, dado el sistema mecánico anterior, cuyo estado está determinado por su posición y velocidad, el espacio de estado para el sistema de la Figura 2.1 será de 2 dimensiones, con una coordenada que repre-senta la posición del sistema
es el vector estado y sus coordenadas son las variables de estado (en el sistema mecánico de la Figura 2.1 sería un vector de 2 coordenadas: posición y velocidad). La variación del vector de estado respecto al tiempo se representa como una función vectorial, generalmente no lineal, cuyo argumento son los vectores de estado y de entrada5 [27]. El conjunto de todos los estados que puede alcanzar un sistema se denomina su espacio de estado. Puesto que cada estado estará caracterizado por un valor concreto de las variables de estado, el espacio de estado tiene por ejes coordenados las variables de estado. Así por ejemplo, dado el sistema mecánico anterior, cuyo estado está determinado por su posición y velocidad, el espacio de estado para el sistema de la Figura 2.1 será de 2 dimensiones, con una coordenada que repre-senta la posición del sistema 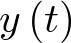 y otra la velocidad
y otra la velocidad 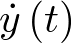 .
.
El modelo de estado se completa con la ecuación de salida (2.4), la cual representa generalmente el conjunto de variables que pueden ser medidas y que constituyen la respuesta del sistema. La ecuación de salida es una función vectorial del vector de estado y del vector de entrada.
 |
(2.4) |
A modo de ejemplo, y por fijar ideas, vamos a escribir el modelo de estado del sistema de la Figura 2.1. En él, como se ha dicho más arriba, una coordenada del vector de estado 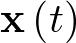 será la posición (sea pues
será la posición (sea pues 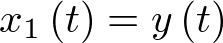 ) y la otra la velocidad (sea pues
) y la otra la velocidad (sea pues 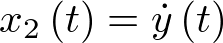 ). Por supuesto el sistema es de orden 2, con lo cual la ecuación de estado en la forma (2.2) constará de dos ecuaciones diferenciales de primer orden, las cuales se obtienen a partir de sustituir las coordenadas del vector de estado en la ecuación (2.2). Esto es:
). Por supuesto el sistema es de orden 2, con lo cual la ecuación de estado en la forma (2.2) constará de dos ecuaciones diferenciales de primer orden, las cuales se obtienen a partir de sustituir las coordenadas del vector de estado en la ecuación (2.2). Esto es:
![\[m{\dot x_2}\left( t \right) + \beta {x_2}\left( t \right) + k{x_1}\left( t \right) = u\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.1-18%282.5%29.png) |
(2.5) |
Cabría preguntarse si se podría haberse sustituido 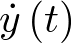 por
por 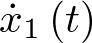 , en vez de por
, en vez de por 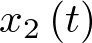 como se ha hecho, sin embargo esta sustitución no cumpliría la ecuación (2.3) que exige una sola coordenada derivada por ecuación.
como se ha hecho, sin embargo esta sustitución no cumpliría la ecuación (2.3) que exige una sola coordenada derivada por ecuación.
A partir de (2.5) basta con despejar la coordenada derivada del vector de estado (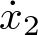 ) y tener en cuenta que
) y tener en cuenta que 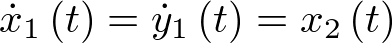 , de modo que la ecuación de estado del sistema de la Figura 2.1 en la forma
, de modo que la ecuación de estado del sistema de la Figura 2.1 en la forma 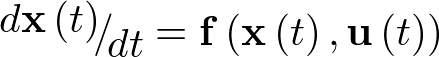 será:
será:
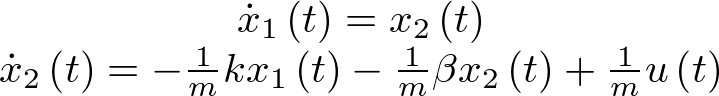 |
(2.6) |
Nótese que la entrada u(t) al sistema es un escalar en este caso. El modelo de estado se completa con la ecuación de salida en la forma (2.4), que en este caso estará dada por 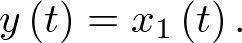
Al ser el modelo de estado lineal6 [28], éste, a partir de la ecuación (2.5) y la de salida, admite una representación matricial de la forma:
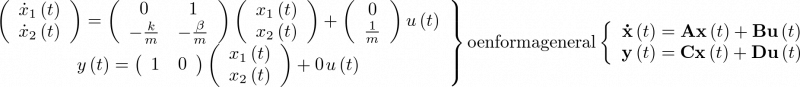 |
(2.7) |
Donde A es una matriz de orden ![\[n \times n\]](/antonio.barragan/files/archivos_usuarios/78/form2.1-28.png) , siendo n la dimensión del espacio de estado u orden del sistema (2 en el ejemplo). B es una matriz de orden
, siendo n la dimensión del espacio de estado u orden del sistema (2 en el ejemplo). B es una matriz de orden ![\[n \times p\]](/antonio.barragan/files/archivos_usuarios/78/form2.1-29.png) , siendo p el número de entradas del sistema, 1 en este caso. Respecto de la ecuación de salida, C es una matriz de orden
, siendo p el número de entradas del sistema, 1 en este caso. Respecto de la ecuación de salida, C es una matriz de orden ![\[q \times n\]](/antonio.barragan/files/archivos_usuarios/78/form2.1-30.png) , siendo m las salidas del sistema (1 en el ejemplo). Por último, la matriz D (0 en este caso) es de orden
, siendo m las salidas del sistema (1 en el ejemplo). Por último, la matriz D (0 en este caso) es de orden ![\[q \times p\]](/antonio.barragan/files/archivos_usuarios/78/form2.1-31.png) . Normalmente los modelos de estado no tienen matriz D, lo cual indica que, como suele ser habitual, la entrada no influencia de modo directo a la salida.
. Normalmente los modelos de estado no tienen matriz D, lo cual indica que, como suele ser habitual, la entrada no influencia de modo directo a la salida.
A continuación se van a formalizar los conceptos introducidos en la sección anterior. Esto se hará para el dominio de tiempo continuo (ecuaciones diferenciales); para el dominio de tiempo discreto (ecuaciones en diferencias) se realizará en la sección 2.5.
Tiempo continuo
El estado de un sistema es una colección de variables, denominadas variables de estado, que reúnen la información suficiente sobre el pasado del mismo, de tal manera que su conocimiento en el instante actual 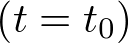 junto con el de la entrada para el momento presente y futuro
junto con el de la entrada para el momento presente y futuro 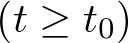 , permite determinar el comportamiento del sistema para cualquier
, permite determinar el comportamiento del sistema para cualquier  .
.
Las variables de estado componen un vector ![\[{\mathbf{x}}\left( t \right) \in {\mathbb{R}^n}\]](/antonio.barragan/files/archivos_usuarios/78/form2.1.2-35.png) denominado vector de estado. Las variables de control (o de entrada) forman el vector de entrada
denominado vector de estado. Las variables de control (o de entrada) forman el vector de entrada ![\[{\mathbf{u}}\left( t \right) \in {\mathbb{R}^p}\]](/antonio.barragan/files/archivos_usuarios/78/form2.1.2-36.png) , y las señales medidas (respuestas) constituyen el vector de salida
, y las señales medidas (respuestas) constituyen el vector de salida 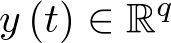 . A partir de aquí, un sistema dinámico invariante con el tiempo7 [29] puede ser representado por las ecuaciones:
. A partir de aquí, un sistema dinámico invariante con el tiempo7 [29] puede ser representado por las ecuaciones:
 |
(2.8) |
Donde ![\[{\raise0.7ex\hbox{${d{\mathbf{x}}}$} \!\mathord{\left/ {\vphantom {{d{\mathbf{x}}} {dt}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${dt}$}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.1.2-40.png) representa un conjunto de n ecuaciones diferenciales ordinarias.
representa un conjunto de n ecuaciones diferenciales ordinarias. 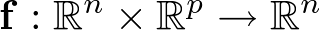 y
y 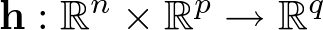 son funciones vectoriales generalmente no lineales. Un modelo de la forma (2.8) se denomina modelo de estado. A esta forma de representar un sistema dinámico se le denomina representación interna, ya que las coordenadas de vector de estado son variables que en todo o en parte no estarán presentes en los terminales de salida del sistema.
son funciones vectoriales generalmente no lineales. Un modelo de la forma (2.8) se denomina modelo de estado. A esta forma de representar un sistema dinámico se le denomina representación interna, ya que las coordenadas de vector de estado son variables que en todo o en parte no estarán presentes en los terminales de salida del sistema.
La dimensión del vector de estado viene dada por el orden del sistema. El sistema (2.8) se denomina invariante con el tiempo porque las funciones f y h no dependen explícitamente del tiempo. Por supuesto, hay modelos más generales donde esta dependencia explícita sí se da. Como se puede apreciar en la ecuación (2.8), el modelo de estado consta de dos funciones: la función f da la variación temporal del vector de estado como una función del estado 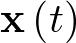 y la ley de control
y la ley de control 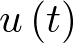 , y la función h da los valores medidos como una función del estado
, y la función h da los valores medidos como una función del estado 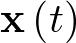 y la ley de control
y la ley de control 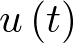 .
.
Un modelo de estado se denomina lineal si las funciones f y h son lineales en 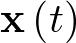 y
y 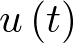 Esto permite escribir el modelo (2.8) en la forma:
Esto permite escribir el modelo (2.8) en la forma:
 |
(2.9) |
Donde A, B, C y D son matrices constantes. La matriz A se denomina matriz de estado o matriz dinámica (de dimensión 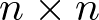 ), la matriz B se denomina matriz de entrada o matriz de control (de dimensión
), la matriz B se denomina matriz de entrada o matriz de control (de dimensión 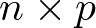 ), la matriz C se denomina matriz de salida o matriz sensora (de dimensión
), la matriz C se denomina matriz de salida o matriz sensora (de dimensión 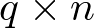 ), y la matriz D se denomina matriz de transferencia directa o simplemente término directo (de dimensión
), y la matriz D se denomina matriz de transferencia directa o simplemente término directo (de dimensión 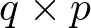 ).
).
Como se ha visto, el modelo de estado se obtiene a partir de la ecuación diferencial que captura la dinámica del sistema. En consecuencia, dependiendo de la forma que tenga la ecuación dife-rencial se pueden obtener modelos de estado diferentes, los cuales, una vez conocida la metodo-logía, pueden ser obtenidos de forma directa a partir de la ecuación diferencial de partida.
Sea por ejemplo un sistema de orden n en el que la señal de control no contiene términos deri-vados:
|
o en notación abreviada: |
(2.10) |
Si se define
![${\bf{x}}\left( t \right)\,\, = {\left[ {{x_1}\left( t \right)\,\,{x_2}\left( t \right) \ldots \,{x_n}\left( t \right)} \right]^{\rm{T}}} = \left[ {y\left( t \right)\,\,\dot y\left( t \right) \ldots {y^{\left( {n - 1} \right)}}\left( t \right)} \right]{\,^{\rm{T}}}\,\,\,\,\,\,\,$](/antonio.barragan/files/archivos_usuarios/78/form2.1.2-48%282.11%29.png) |
(2.11) |
Entonces, la ecuación (2.10) puede ser escrita como
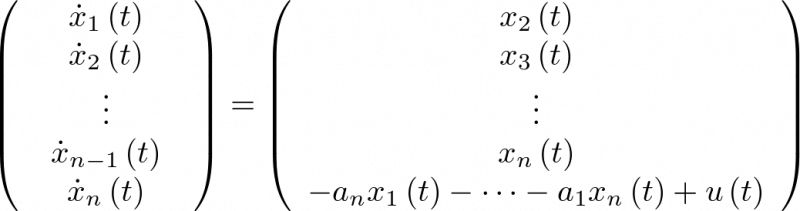 |
(2.12) |
O bien en la forma 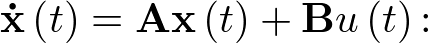
 |
(2.13) |
Por último, la ecuación de salida se escribirá:
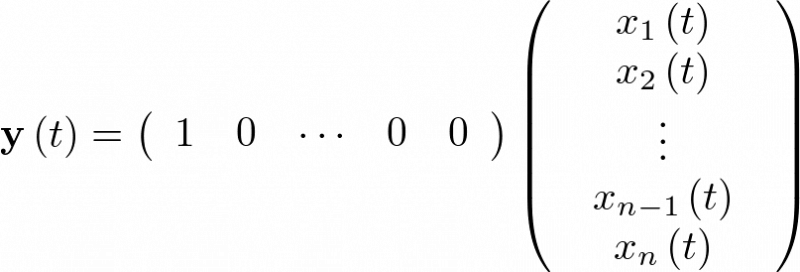 |
(2.14) |
La forma de elección de variables de estado que da lugar al modelo representado en (2.13) y (2.14) se denomina forma canónica de cadena de integradores, o forma canónica de control. Existen muchas más formas de obtener representaciones en el espacio de estado de los sistemas. Algu-nas de ellas se irán viendo conforme sea apropiado a lo largo del texto.
Con objeto de fijar ideas vamos a realizar ahora varios ejercicios de modelado de sistemas di-námicos de diferente índole.
Ejemplo 2.2. Propagación de una enfermedad epidémica. La propagación de una enfermedad epidémica puede ser descrita mediante un conjunto de ecuaciones diferenciales de primer orden. Asúmase que el vector población de estudio  tiene 3 coordenadas: población en riesgo de ser infectada
tiene 3 coordenadas: población en riesgo de ser infectada 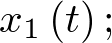 población infectada
población infectada 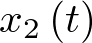 y población que no va a ser infectada
y población que no va a ser infectada 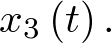 Este último grupo reúne a las personas que son inmunes a la enfermedad, las que ya han fallecido y las que han conseguido ser aisladas para evitar contagios.
Este último grupo reúne a las personas que son inmunes a la enfermedad, las que ya han fallecido y las que han conseguido ser aisladas para evitar contagios.
Si se asume en primera instancia que la población está aislada y el número de individuos es N, está claro que para todo t se cumplirá que 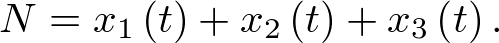 Con objeto de elaborar el modelo dinámico razonaremos del modo siguiente: a partir de un instante de tiempo t en el que el número de infectados es
Con objeto de elaborar el modelo dinámico razonaremos del modo siguiente: a partir de un instante de tiempo t en el que el número de infectados es 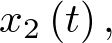 el número de casos nuevos ocurridos en el intervalo
el número de casos nuevos ocurridos en el intervalo ![$\left[ {t,\,\,t + \Delta t} \right]$](/antonio.barragan/files/archivos_usuarios/78/form2.1.2-57.png) será
será 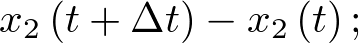 por tanto, la evolución de cada una de las tres poblaciones será:
por tanto, la evolución de cada una de las tres poblaciones será:
![\[\begin{array}{l} {x_1}\left( {t + \Delta t} \right) = {x_1}\left( t \right) - \left\{ {{\rm{Excluidos hacia}}\,\,{x_3}} \right\} - \left\{ {{\rm{Excluidos hacia}}\,\,{x_2}} \right\} \\ {x_2}\left( {t + \Delta t} \right) = {x_2}\left( t \right) + \left\{ {{\rm{Contagiados desde}}\,\,{x_1}} \right\} - \left\{ {{\rm{Excluidos hacia}}\,\,{x_3}} \right\} \\ {x_3}\left( {t + \Delta t} \right) = {x_3}\left( t \right) + \left\{ {{\rm{Excluidos desde}}\,\,{x_1}} \right\} + \left\{ {{\rm{Excluidos desde}}\,\,{x_2}} \right\} \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.1.2-59%282.15%29.png) |
(2.15) |
Esto es,
![\[\begin{array}{l} {x_1}\left( {t + \Delta t} \right) = {x_1}\left( t \right) - \alpha {x_1}\left( t \right)\Delta t - \beta {x_2}\left( t \right)\Delta t \\ {x_2}\left( {t + \Delta t} \right) = {x_2}\left( t \right) + \lambda {x_1}\left( t \right)\Delta t - \gamma {x_2}\left( t \right)\Delta t \\ {x_3}\left( {t + \Delta t} \right) = {x_3}\left( t \right) + \alpha {x_1}\left( t \right)\Delta t + \gamma {x_2}\left( t \right)\Delta t \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.1.2-60%282.16%29.png) |
(2.16) |
Donde los parámetros ![\[\alpha ,\,\beta ,\,\lambda \,\,{\rm{y}}\,\,\gamma \]](/antonio.barragan/files/archivos_usuarios/78/form2.1.2-61.png) son tasas, y obviamente,
son tasas, y obviamente, ![\[\lambda {x_1}\left( t \right)\Delta t = \beta {x_2}\left( t \right)\Delta t.\]](/antonio.barragan/files/archivos_usuarios/78/form2.1.2-62.png) A partir de aquí, teniendo en cuenta que:
A partir de aquí, teniendo en cuenta que:
![\[{\dot x_i}\left( t \right) = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{{x_i}\left( {t + \Delta t} \right) - {x_i}\left( t \right)}}{{\Delta t}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.1.2-63%282.17%29.png) |
(2.17) |
Podemos escribir el modelo de estado del sistema que representa la propagación de la epidemia como
![\[\left. \begin{array}{l} {{\dot x}_1}\left( t \right) = - \alpha {x_1}\left( t \right) - \beta {x_2}\left( t \right) \\ {{\dot x}_2}\left( t \right) = \lambda {x_1}\left( t \right) - \gamma {x_2}\left( t \right) \\ {{\dot x}_3}\left( t \right) = \alpha {x_1}\left( t \right) + \gamma {x_2}\left( t \right) \\ \end{array} \right\} \Rightarrow \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ {{{\dot x}_3}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} \hfill { - \alpha } & \hfill { - \beta } & \hfill 0 \\ \hfill \lambda & \hfill { - \gamma } & \hfill 0 \\ \hfill \alpha & \hfill \gamma & \hfill 0 \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ {{x_3}\left( t \right)} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.1.2-64%282.18%29.png) |
(2.18) |
Si consideramos ahora que el sistema no está aislado, de modo que 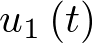 es la velocidad con la que se incorporan nuevos individuos a la población con riesgo, y
es la velocidad con la que se incorporan nuevos individuos a la población con riesgo, y 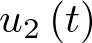 la velocidad con la que se añaden nuevos individuos a la población infectada, la ecuación (2.18) se escribirá en la forma:
la velocidad con la que se añaden nuevos individuos a la población infectada, la ecuación (2.18) se escribirá en la forma:
![\[\left. \begin{array}{l} {{\dot x}_1}\left( t \right) = - \alpha {x_1}\left( t \right) - \beta {x_2}\left( t \right) + {u_1}\left( t \right) \\ {{\dot x}_2}\left( t \right) = \lambda {x_1}\left( t \right) - \gamma {x_2}\left( t \right) + {u_2}\left( t \right) \\ {{\dot x}_3}\left( t \right) = \alpha {x_1}\left( t \right) + \gamma {x_2}\left( t \right) \\ \end{array} \right\} \Rightarrow \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ {{{\dot x}_3}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} \hfill { - \alpha } & \hfill { - \beta } & \hfill 0 \\ \hfill \lambda & \hfill { - \gamma } & \hfill 0 \\ \hfill \alpha & \hfill \gamma & \hfill 0 \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ {{x_3}\left( t \right)} \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} \hfill 1 & \hfill 0 \\ \hfill 0 & \hfill 1 \\ \hfill 0 & \hfill 0 \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{u_1}\left( t \right)} \\ {{u_2}\left( t \right)} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.1.2-67%282.19%29.png) |
(2.19) |
Nótese que los modelos (2.18) y (2.19) son simples en el sentido que son lineales, ya que no in-cluyen la interacción entre los grupos 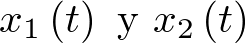 . Volveremos con esto más adelante, en el ejemplo 2.13.
. Volveremos con esto más adelante, en el ejemplo 2.13.
 |
| Figura 2.2. Sistema péndulo. |
Ejemplo 2.3. Sistema péndulo. Considere el péndulo simple de la Figura 2.2, el cual está sujeto por una cuerda inextensible de longitud l y masa despreciable. El péndulo está sometido a la fuerza gravitacional mg debida a su peso, y a la fuerza de fricción 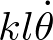 , la cual se asume que es proporcional a la velocidad con un coeficiente de fricción k. La aplicación de la segunda ley de Newton (expresión (2.1)) permite escribir la ecuación del movimiento en la dirección tangencial:
, la cual se asume que es proporcional a la velocidad con un coeficiente de fricción k. La aplicación de la segunda ley de Newton (expresión (2.1)) permite escribir la ecuación del movimiento en la dirección tangencial:
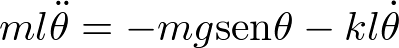 |
(2.20) |
Como se sabe, siempre que sea posible hay que intentar elegir un eje coordenado que sea paralelo a la aceleración. En este caso, la escritura del movimiento en la dirección tangencial tiene la ventaja que la tensión en la cuerda, la cual es normal, no aparece en la ecuación. Para obtener el modelo de estado del péndulo tomaremos como siempre las coordenadas posición y velocidad para el vector de estado, esto es, 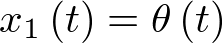 y
y 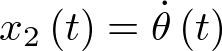 . Entonces, el modelo de estado es:
. Entonces, el modelo de estado es:
![\[\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right) = {x_2}\left( t \right)} \\ {{{\dot x}_2}\left( t \right) = - \frac{g}{l}{\rm{sen}}{x_1}\left( t \right) - \frac{k}{m}{x_2}\left( t \right)} \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.1.2-74%282.21%29.png) |
(2.21) |
Nótese el carácter no lineal del modelo de estado que, consecuentemente, no admite escritura en forma matricial.
 |
| Figura 2.3. Circuito RLC con fuente de corriente. |
Ejemplo 2.4. Circuito RLC. Veamos ahora un sistema eléctrico. Sea pues el circuito RLC de la Figura 2.3. Si en los modelos de estado de los sistemas mecánicos las variables de estado a con-siderar son la posición y velocidad, en los circuitos eléctricos interesa considerar la corriente y/o tensión en los elementos almacenadores de energía. Entonces, asumiendo que el condensador e inductor son elementos ideales, sus modelos de circuito están dados, respectivamente, por 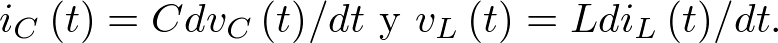 Sea pues
Sea pues 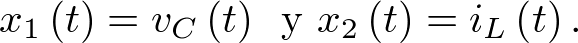 La entrada del sistema es la fuente de corriente
La entrada del sistema es la fuente de corriente 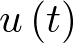 y la salida la tensión en la carga
y la salida la tensión en la carga 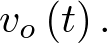 Según lo anterior, el modelo de estado puede ser planteado del modo siguiente:
Según lo anterior, el modelo de estado puede ser planteado del modo siguiente:
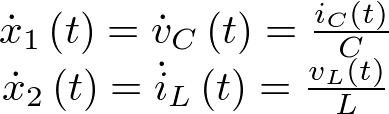 |
(2.22) |
Ahora, aplicando las leyes de Kirchhoff de corriente y tensión se establecen las relaciones que permiten escribir (2.22) en la forma  Así, aplicando la ley de Kirchhoff de co-rriente en el nudo superior de la Figura 2.3 se tiene que:
Así, aplicando la ley de Kirchhoff de co-rriente en el nudo superior de la Figura 2.3 se tiene que:
 |
(2.23) |
Esto es,
 |
(2.24) |
La expresión anterior permite completar la primera ecuación de estado de (2.22). Respecto de la segunda, ésta se completa aplicando la ley de Kirchhoff de tensiones al lazo RLC. En él se cumple que
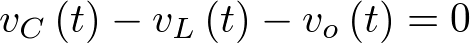 |
(2.25) |
Esto es,
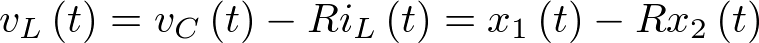 |
(2.26) |
Sustituyendo (2.24) y (2.26) en la ecuación de estado (2.22) se tiene que
![\[\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right) = - \frac{1}{C}{x_2}\left( t \right) + \frac{1}{C}u\left( t \right)} \\ {{{\dot x}_2}\left( t \right) = \frac{1}{L}{x_1}\left( t \right) - \frac{R}{L}{x_2}\left( t \right)} \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.1.2-85%282.27%29.png) |
(2.27) |
Respecto de la ecuación de salida está dada por
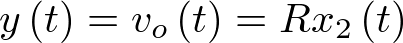 |
(2.28) |
El conjunto de ecuaciones (2.27) y (2.28) permite escribir el modelo de estado del circuito del modo siguiente:
![\[\left. {\begin{array}{*{20}{c}} {{\bf{\dot x}}\left( t \right) = {\bf{Ax}}\left( t \right) + {\bf{B}}u\left( t \right)} \\ {y\left( t \right) = {\bf{Cx}}\left( t \right)} \\ \end{array}} \right\} \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 & { - \frac{1}{C}} \\ {\frac{1}{L}} & { - \frac{R}{L}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {\frac{1}{C}} \\ 0 \\ \end{array}} \right)u\left( t \right)} \\ {y\left( t \right) = \left( {\begin{array}{*{20}{c}} 0 & R \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right)} \\ \end{array}} \right.\]](/antonio.barragan/files/archivos_usuarios/78/form2.1.2-87%282.29%29.png) |
(2.29) |
Es importante tener muy presente los conceptos lineal y no lineal. La consideración de lineal para un modelo y las expresiones matemáticas que lo definen facilita mucho su manejo y comprensión. Sin embargo, teniendo en cuenta que, en general, los sistemas reales son no lineales, el grado de aproximación que se requiere para convertir un sistema no lineal en lineal siempre ha de ser tenido en cuenta. Como muestra, cuando en el ejemplo 2.1 se asume que el comportamiento del muelle es lineal, debemos tener en cuenta que esto exige, para que el modelo tenga suficiente precisión, que los esfuerzos aplicados sobre el muelle sean pequeños, lo cual ya nos está indicando que el modelo lineal deducido en el ejemplo no es válido para cualquier condición de funcionamiento.
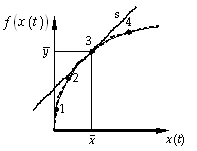 |
| Figura 2.4. Linealización a tramos |
Linealizar un sistema no lineal es una técnica habitual que ayuda mucho en el análisis de los sistemas no lineales, sin embargo, nunca hay que perder de vista el ámbito de validez del modelo lineal y el error que se comete. Véase por ejemplo la Figura 2.4, donde la función no lineal 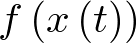 ha sido linealizada a tramos en el entorno de diferentes puntos de operación (1 a 4). Esto se ha hecho así porque el error que se comete es mucho menor que si se linealiza la función en un solo tramo para todo el dominio de interés (segmento s). Dicho esto, hay que tener en cuenta ahora que la función no lineal
ha sido linealizada a tramos en el entorno de diferentes puntos de operación (1 a 4). Esto se ha hecho así porque el error que se comete es mucho menor que si se linealiza la función en un solo tramo para todo el dominio de interés (segmento s). Dicho esto, hay que tener en cuenta ahora que la función no lineal 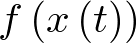 podrá ser aproximada mediante 4 expresiones linealizadas, cada una de las cuales sólo será válida en su dominio correspondiente (entorno de los puntos 1 a 4); por tanto, dependiendo del tramo de operación, el modelo lineal a aplicar deberá ser el apropiado, ya que en caso contrario los errores cometidos podrían hacer inoperativo el modelo. Así por ejemplo, si el sistema no lineal va a trabajar en torno a un punto de operación (supongamos
podrá ser aproximada mediante 4 expresiones linealizadas, cada una de las cuales sólo será válida en su dominio correspondiente (entorno de los puntos 1 a 4); por tanto, dependiendo del tramo de operación, el modelo lineal a aplicar deberá ser el apropiado, ya que en caso contrario los errores cometidos podrían hacer inoperativo el modelo. Así por ejemplo, si el sistema no lineal va a trabajar en torno a un punto de operación (supongamos  punto 3 de la Figura 2.4) con pequeños desplazamientos alrededor de él, el modelo lineal a utilizar será el que describe dicho entorno, no siendo necesarios el resto de modelos por ser puntos de operación en los que no se va a encontrar el sistema.
punto 3 de la Figura 2.4) con pequeños desplazamientos alrededor de él, el modelo lineal a utilizar será el que describe dicho entorno, no siendo necesarios el resto de modelos por ser puntos de operación en los que no se va a encontrar el sistema.
Una técnica habitual de linealización de funciones no lineales consiste en realizar un desarrollo en serie de Taylor de la expresión no lineal alrededor de un punto de operación concreto. Así por ejemplo, si como en la Figura 2.4 se considera que el punto de operación normal es  la ecuación no lineal
la ecuación no lineal 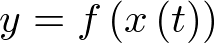 puede ser desarrollada alrededor de ese punto del modo siguiente:
puede ser desarrollada alrededor de ese punto del modo siguiente:
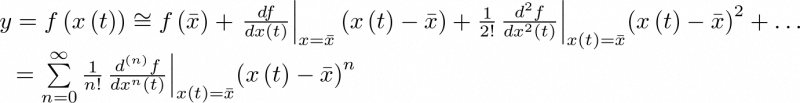 |
(2.30) |
Si la variación 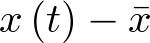 es pequeña (validez de la aproximación de la curva mediante el segmento), los términos de orden superior en
es pequeña (validez de la aproximación de la curva mediante el segmento), los términos de orden superior en 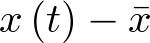 pueden ser obviados, con lo cual la ecuación (2.30) puede ser escrita abreviadamente como
pueden ser obviados, con lo cual la ecuación (2.30) puede ser escrita abreviadamente como
![\[y\left( t \right) \simeq f\left( {\bar x} \right) + K\left( {x\left( t \right) - \bar x} \right);{\rm{ donde }}K = {\left. {\frac{{df}}{{dx\left( t \right)}}} \right|_{x\left( t \right) = \bar x}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.2-5%282.31%29.png) |
(2.31) |
Esto es, puesto que 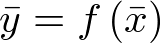 , la ecuación (2.31) puede ser escrita como
, la ecuación (2.31) puede ser escrita como
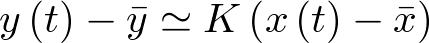 |
(2.32) |
Lo cual indica que 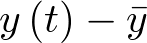 es sensiblemente proporcional a
es sensiblemente proporcional a 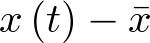 ; esto es, (2.32) es un modelo lineal aproximado de
; esto es, (2.32) es un modelo lineal aproximado de 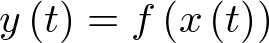 válido en el entorno
válido en el entorno 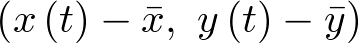 del punto de operación.
del punto de operación.
Si f es una función de varias variables, supongamos dos por ejemplo8 [30], el desarrollo en serie de Taylor de 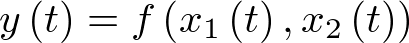 se escribiría, en el entorno de un punto de interés
se escribiría, en el entorno de un punto de interés 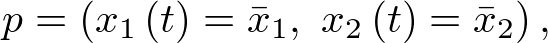 como
como
![\[\begin{array}{*{20}{c}} {y\left( t \right) \cong f\left( {{x_1}\left( t \right),{x_2}\left( t \right)} \right) = f\left( {{{\bar x}_1},{{\bar x}_2}} \right) + \left[ {{{\left. {\frac{{\partial f}}{{\partial {x_1}\left( t \right)}}} \right|}_p}\left( {{x_1}\left( t \right) - {{\bar x}_1}} \right) + {{\left. {\frac{{\partial f}}{{\partial {x_2}\left( t \right)}}} \right|}_p}\left( {{x_2}\left( t \right) - {{\bar x}_2}} \right)} \right]} \hfill \\ { + \frac{1}{{2{\rm{!}}}}\left[ {{{\left. {\frac{{{\partial ^2}f}}{{\partial {x_1}^2\left( t \right)}}} \right|}_p}{{\left( {{x_1}\left( t \right) - {{\bar x}_1}} \right)}^2} + 2{{\left. {\frac{{{\partial ^2}f}}{{\partial {x_1}\left( t \right)\partial {x_2}\left( t \right)}}} \right|}_p}\left( {{x_1}\left( t \right) - {{\bar x}_1}} \right)\left( {{x_2}\left( t \right) - {{\bar x}_2}} \right) + {{\left. {\frac{{{\partial ^2}f}}{{\partial {x_2}^2\left( t \right)}}} \right|}_p}{{\left( {{x_2}\left( t \right) - {{\bar x}_2}} \right)}^2}} \right] + \cdots } \hfill \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.2-14%282.33%29.png) |
(2.33) |
Nuevamente, puesto que 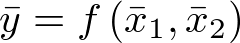 , la ecuación (2.33) puede ser escrita, despreciando los términos de orden superior, como un modelo matemático lineal válido alrededor del punto de operación p:
, la ecuación (2.33) puede ser escrita, despreciando los términos de orden superior, como un modelo matemático lineal válido alrededor del punto de operación p:
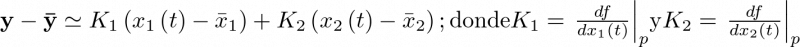 |
(2.34) |
Ejemplo 2.5. Linealización de un modelo no lineal. Sea la ecuación no lineal ![\[y = f\left( {{x_1},{x_2}} \right) = {x_1}{x_2}\]](/antonio.barragan/files/archivos_usuarios/78/form2.2-17.png) . Se trata de linealizarla en la región
. Se trata de linealizarla en la región ![\[4 \le {x_1} \le 8{\rm{ y }}9 \le {x_2} \le 13.\]](/antonio.barragan/files/archivos_usuarios/78/form2.2-18.png) El punto lógico de operación para realizar la linealización es el medio en ambas regiones, esto es:
El punto lógico de operación para realizar la linealización es el medio en ambas regiones, esto es: ![\[{\bar x_1} = 6{\rm{ y }}{\bar x_2} = 11.\]](/antonio.barragan/files/archivos_usuarios/78/form2.2-19.png) Aplicando (2.34) se tiene que
Aplicando (2.34) se tiene que
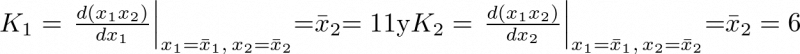 |
(2.35) |
La ecuación linealizada es pues
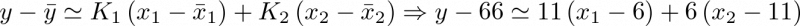 |
(2.36) |
Donde 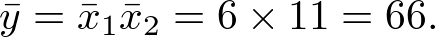 La ecuación (2.36) puede ser escrita también como
La ecuación (2.36) puede ser escrita también como
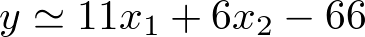 |
(2.37) |
Para 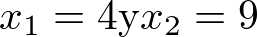 por ejemplo, el valor verdadero de y es
por ejemplo, el valor verdadero de y es  . El valor linealizado se obtiene de (2.37) y vale
. El valor linealizado se obtiene de (2.37) y vale 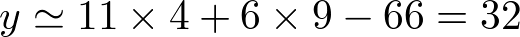 . Por tanto, en este punto el error cometido es de
. Por tanto, en este punto el error cometido es de 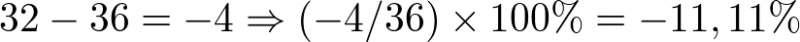 . En el otro extremo,
. En el otro extremo, 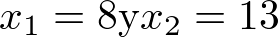 ,con lo cual el valor real de y es
,con lo cual el valor real de y es 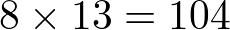 , y el aproximado
, y el aproximado  . Aquí el error es menor que en el otro extremo:
. Aquí el error es menor que en el otro extremo: 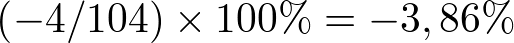 .
.
En ingeniería de control es de gran interés la linealización de la ecuación de estado, ya que ello permite linealizar en torno a un punto el modelo de un sistema no lineal. La ecuación de estado, como se sabe, es una función vectorial de varias variables, lo cual hace que su procedimiento de linealización sea un poco más complejo que el visto en esta sección. Trataremos esta cuestión con detalle en la sección 3.8 del capítulo siguiente.
 |
| Figura 2.5. Sistema de una entrada – una salida (SISO). |
La función de transferencia de un sistema lineal e invariante en el tiempo se define como la relación entre la transformada de Laplace9 [31] de la variable de salida y la transformada de Laplace de la variable de entrada, suponiendo que todas las condiciones iniciales se hacen iguales a cero. Esta forma de representar sistemas se denomina representación externa, ya que atiende a las señales presentes en sus terminales de entrada y salida. Así, dado el sistema de la Figura 2.5, su función de transferencia será:
![$G\left( s \right) = {\left. {\frac{{L\left[ {y\left( t \right)} \right]}}{{L\left[ {u\left( t \right)} \right]}}} \right|_{\scriptstyle {\rm{Cond}}{\rm{.}}\,{\rm{iniciales}} \hfill \atop \scriptstyle {\rm{nulas}} \hfill}} = \frac{{Y\left( s \right)}}{{U\left( s \right)}}$](/antonio.barragan/files/archivos_usuarios/78/form2.3-4%282.38%29.png) |
(2.38) |
 |
| Figura 2.6. Esquema conceptual del proceso de resolución de una ecuación diferencial mediante la transformada de Laplace. |
Tradicionalmente la transformada de Laplace ha sido muy usada en sistemas de control y aún hoy día todavía lo es, sin embargo, restringe mucho el campo de aplicación, ya que sólo es apropiada para estudiar sistemas lineales y, dentro de éstos, los de una entrada-una salida o SISO (del inglés Single Imput-Single Output). Para el caso de sistemas lineales MIMO (del inglés Multiple Imputs-Multiple Outputs), habrá tantas funciones de transferencia como relaciones salida/entrada puedan ser obtenidas. Así por ejemplo, un sistema lineal con dos entradas y dos salidas generará 4 funciones de transferencia: Y1(s)/U1(s), Y1(s)/U2(s), Y2(s)/U1(s), e Y2(s)/U2(s). Evidentemente, la clave para poder hacer esta separación entrada/salida es la imposición de linealidad del sistema, la cual permite obtener la respuesta total como la suma de las respuestas individuales entre cada entrada y salida.
A continuación, con objeto de fijar ideas y familiarizar al lector no avezado en el uso operacional de la transformada de Laplace, vamos a realizar un par de ejemplos donde se pone de manifiesto su utilidad. Las ocasiones en las que se use la transformada de Laplace en el texto se hará siempre como herramienta, por tanto, se recomienda el manejo de otros libros para profundizar en este instrumento matemático.
Ejemplo 2.6. Resolución de una ecuación diferencial lineal ordinaria. La transformada de Laplace facilita de forma notable la resolución de ecuaciones diferenciales lineales, ya que convierte la ecuación diferencial temporal en un polinomio en s, y el proceso de integración para resolverla, en una manipulación algebraica de un polinomio cuya conversión al dominio temporal es inmediata mediante tablas. El proceso descrito se ilustra en la Figura 2.6. Para realizar la transformación desde el dominio de la variable compleja s al dominio temporal se emplea una integral de inversión denominada transformada inversa10 [32] de Laplace, 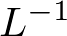 .
.
En la práctica, rara vez se emplea la integral de inversión para encontrar f(t). Hay un método más sencillo que vamos a ilustrar en este ejemplo, que consiste en descomponer la expresión en s resultante de la transformación en fracciones simples, para después, mediante tablas, realizar una traslación directa al dominio temporal. Sea pues la ecuación diferencial a resolver siguiente:
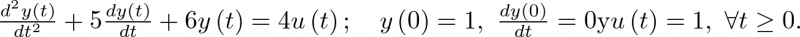 |
(2.39) |
Aplicando la transformada de Laplace11 [33] a cada término de la ecuación:
![\[L\left[ {\frac{{{d^2}y\left( t \right)}}{{d{t^2}}}} \right] + 5L\left[ {\frac{{dy\left( t \right)}}{{dt}}} \right] + 6L\left[ {y\left( t \right)} \right] = 4L\left[ {u\left( t \right)} \right]\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-10%282.40%29.png) |
(2.40) |
Utilizando una tabla de transformadas se escribe la correspondiente a cada sumando:
![\[{s^2}Y\left( s \right) - sy\left( 0 \right) - \frac{{dy\left( 0 \right)}}{{dt}} + 5\left[ {sY\left( s \right) - y\left( 0 \right)} \right] + 6Y\left( s \right) = 4U\left( s \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-11%282.41%29.png) |
(2.41) |
Ahora, teniendo en cuenta las condiciones iniciales y que la transformada de la señal escalón unitario U(s) es 1/s,
![\[{s^2}Y\left( s \right) - s + 5\left[ {sY\left( s \right) - 1} \right] + 6Y\left( s \right) = \frac{4}{s}\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-12%282.42%29.png) |
(2.42) |
Agrupando términos y despejando Y(s),
![\[Y\left( s \right) = \left[ {\frac{{s + 5}}{{{s^2} + 5s + 6}}} \right] + \left[ {\frac{4}{{s\left( {{s^2} + 5s + 6} \right)}}} \right]\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-13%282.43%29.png) |
(2.43) |
Donde  . Entonces, el desarrollo en fracciones parciales12 [34] de la expresión anterior es:
. Entonces, el desarrollo en fracciones parciales12 [34] de la expresión anterior es:
![$Y\left( s \right) = \left[ {\frac{A}{{s + 2}} + \frac{B}{{s + 3}}} \right] + \left[ {\frac{C}{{s + 2}} + \frac{D}{{s + 3}} + \frac{E}{s}} \right]$](/antonio.barragan/files/archivos_usuarios/78/form2.3-16%282.44%29.png) |
(2.44) |
Cada uno de los coeficientes de la expresión anterior puede ser obtenido actuando sobre cada fracción de (2.43) y su desarrollo de (2.44) del modo siguiente:
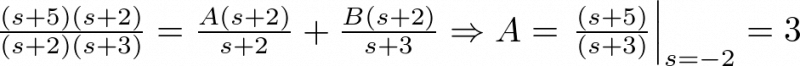 |
(2.45) |
Del mismo modo:
|
|
(2.46) |
Por tanto,
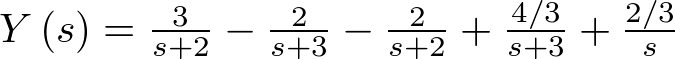 |
(2.47) |
Utilizando una tabla de transformadas se aplica ahora la transformada inversa13 [35] a cada sumando para obtener la solución de la ecuación diferencial (2.39) en el dominio del tiempo:
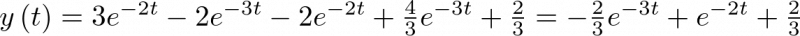 |
(2.48) |
Nótese que conforme el tiempo transcurra los términos exponenciales tenderán a cero, de modo que la respuesta a la que tenderá el sistema (respuesta estacionaria) es 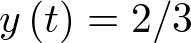 .
.
Ejemplo 2.7. Sistema de amplificador operacional. Sea el sistema de amplificadores operacionales ideales de la Figura 2.7, donde se considera que las resistencias y el condensador son también ideales. Se trata de obtener la función de transferencia 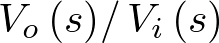 .
.
 |
| Figura 2.7. Integrador. |
 |
| Figura 2.8. Integrador. Circuito trans-formado en s. |
Al ser las resistencias y el condensador ideales, su relación tensión/corriente está dada por 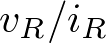 e
e 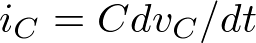 respectivamente. Considerando la salida de estos elementos la tensión y la entrada la corriente podemos, aplicando el concepto de función de transferencia, obtener sus impedancias en el dominio de la transformada de Laplace. Esto es,
respectivamente. Considerando la salida de estos elementos la tensión y la entrada la corriente podemos, aplicando el concepto de función de transferencia, obtener sus impedancias en el dominio de la transformada de Laplace. Esto es, ![\[{{{V_R}\left( s \right)} \mathord{\left/ {\vphantom {{{V_R}\left( s \right)} {{I_R}\left( s \right)}}} \right. \kern-\nulldelimiterspace} {{I_R}\left( s \right)}} = R{\rm{ y }}{{{V_C}\left( s \right)} \mathord{\left/ {\vphantom {{{V_C}\left( s \right)} {{I_C}\left( s \right)}}} \right. \kern-\nulldelimiterspace} {{I_C}\left( s \right)}} = {1 \mathord{\left/ {\vphantom {1 {Cs}}} \right. \kern-\nulldelimiterspace} {Cs}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-26.png) .
.
A partir de aquí, el circuito de la Figura 2.7 puede ser escrito en el dominio de la variable compleja s tal como en la Figura 2.8. Al ser los amplificadores operacionales ideales: 1) se considera el cortocircuito virtual a su entrada, con lo cual la entrada inversora está al potencial de referencia, y 2) la impedancia de entrada es infinita, de modo que sólo circula corriente por el lazo de realimentación. Bajo estas premisas se tiene que
![\[\frac{{{V_i}\left( s \right)}}{{{R_1}}} = - \frac{{{V_a}\left( s \right)}}{{{1 \mathord{\left/ {\vphantom {1 {Cs}}} \right. \kern-\nulldelimiterspace} {Cs}}}}{\rm{ y }}\frac{{{V_a}\left( s \right)}}{{{R_2}}} = - \frac{{{V_o}\left( s \right)}}{{{R_3}}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-27%282.49%29.png) |
(2.49) |
Sustituyendo en la primera ecuación anterior el valor de Va(s) de la segunda, se tiene la función de transferencia buscada:
![\[\frac{{{V_o}\left( s \right)}}{{{V_i}\left( s \right)}} = \frac{{{R_3}}}{{{R_2}}}\frac{1}{{{R_1}Cs}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-28%282.50%29.png) |
(2.50) |
El circuito de la figura 2.7 se denomina integrador porque la señal de salida es la integral de la de la entrada multiplicada por una constante. Esto es:
![${V_o}\left( s \right) = \frac{{{R_3}}}{{{R_2}}}\frac{1}{{{R_1}Cs}}{V_i}\left( s \right);\,\,{\rm{pero }}L\left[ {\int_0^t {f\left( t \right)} dt} \right] = \frac{{F\left( s \right)}}{s}.{\rm{ Por tanto}}{\rm{, }}{L^{ - 1}}\left[ {{V_o}\left( s \right)} \right] = \frac{{{R_3}}}{{{R_1}{R_2}C}}\int_0^t {{v_i}\left( t \right)} \,dt$](/antonio.barragan/files/archivos_usuarios/78/form2.3-29%282.51%29.png) |
(2.51) |
Obtención de la función de transferencia a partir del modelo de estado
Realizados los ejemplos volvamos pues con el objeto de esta sección: obtener la función de transferencia de un sistema de una única entrada y una única salida (SISO) definido por su modelo de estado. Sea éste:
![\[\begin{array}{l} {\bf{\dot x}} = {\bf{Ax}} + {\bf{B}}u \\ y = {\bf{Cx}} + {\bf{D}}u \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-30%282.52%29.png) |
(2.52) |
Aplicando la transformada de Laplace a la ecuación de estado y a la ecuación de salida anteriores, se tiene que
![\[\begin{array}{l} s{\bf{X}}\left( s \right) = {\bf{AX}}\left( s \right) + {\bf{B}}U\left( s \right) \\ Y\left( s \right) = {\bf{CX}}\left( s \right) + {\bf{D}}U\left( s \right) \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-31%282.53%29.png) |
(2.53) |
Donde B es una matriz de orden nx1 debido a que el sistema tiene una única entrada u. Obsérvese que no se tienen en cuenta las condiciones iniciales, ya que lo que se busca es una función de transferencia. Reordenando la ecuación de estado anterior se obtiene que
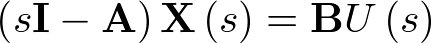 |
(2.54) |
Asumiendo la invertibilidad de la matriz  de orden
de orden 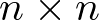 , y denominando su inversa
, y denominando su inversa 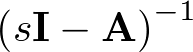 como
como 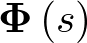 , se tiene
, se tiene
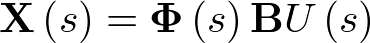 |
(2.55) |
Sustituyendo ahora el valor de X(s) obtenido en la ecuación de salida (2.53), se obtiene
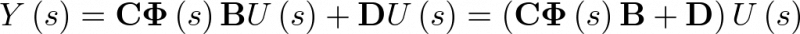 |
(2.56) |
Por consiguiente, la función de transferencia del sistema  es
es
![\[G\left( s \right) = {\bf{C\Phi }}\left( s \right){\bf{B}} + {\bf{D}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-40%282.57%29.png) |
(2.57) |
Puesto que
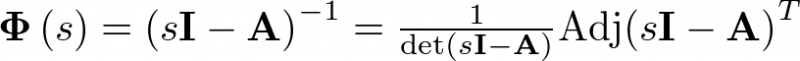 |
(2.58) |
Queda claro que el polinomio denominador de la función de transferencia es 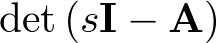 . Esto es, los polos14 [36] del sistema coinciden con los valores propios o autovalores de la matriz A, ya que se obtienen a partir de su ecuación característica o polinomio característico. En conclusión, los polos del sistema dependen sólo de la matriz A, mientras que los ceros15 [37] dependen de las matrices A, B, C y D.
. Esto es, los polos14 [36] del sistema coinciden con los valores propios o autovalores de la matriz A, ya que se obtienen a partir de su ecuación característica o polinomio característico. En conclusión, los polos del sistema dependen sólo de la matriz A, mientras que los ceros15 [37] dependen de las matrices A, B, C y D.
Llegados a este punto cabría preguntarse por la utilidad de la expresión (2.57); la respuesta es inmediata: permite obtener de forma directa la función de transferencia de un modelo de estado lineal de una entrada y una salida (SISO).
Comentario: Desde el punto de vista de los autores, si bien el concepto de la transformada de Laplace es de mucha utilidad en ingeniería de control (y en general en automática), y más aún el de función de transferencia que se deriva del primero, se ha preferido introducir los conceptos en el texto desde lo general a lo particular. Así, mientras el modelo de estado descrito por la expresión (2.8) es absolutamente genera (no lineal y MIMO); el modelo de estado que posibilita la aplicación de la expresión (2.57) es bastante más restrictivo (lineal y SISO).
Una vez sentadas las bases de los ámbitos de uso de las expresiones deducidas, se realizará un ejemplo de aplicación de la expresión (2.57).
Ejemplo 2.8. Función de transferencia de un modelo de estado. Sea el modelo de estado que se dedujo en el Ejemplo 2.1, el cual está dado por la ecuación (2.7). Por comodidad, se escribe de nuevo a continuación.
![\[\left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 & 1 \\ { - \frac{k}{m}} & { - \frac{\beta }{m}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ {\frac{1}{m}} \\ \end{array}} \right)u\left( t \right){\rm{ e }}y\left( t \right) = \left( {\begin{array}{*{20}{c}} 1 & 0 \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) + 0{\kern 1pt} u\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-43%282.59%29.png) |
(2.59) |
Para este caso se tiene pues que
![\[\left( {s{\rm{I}} - {\rm{A}}} \right) = \left( {\left( {\begin{array}{*{20}{c}} s & 0 \\ 0 & s \\ \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 0 & 1 \\ { - \frac{k}{m}} & { - \frac{\beta }{m}} \\ \end{array}} \right)} \right) = \left( {\begin{array}{*{20}{c}} s & { - 1} \\ {\frac{k}{m}} & {s + \frac{\beta }{m}} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-44%282.60%29.png) |
(2.60) |
Por consiguiente,
![\[{\bf{\Phi }}\left( s \right) = {\left( {s{\rm{I}} - {\rm{A}}} \right)^{ - 1}} = \frac{1}{{\Delta \left( s \right)}}\left( {\begin{array}{*{20}{c}} {s + \frac{\beta }{m}} & 1 \\ { - \frac{k}{m}} & s \\ \end{array}} \right);{\rm{ donde }}\Delta \left( s \right) = \left| {\begin{array}{*{20}{c}} s & { - 1} \\ {\frac{k}{m}} & {s + \frac{\beta }{m}} \\ \end{array}} \right| = {s^2} + \frac{\beta }{m}s + \frac{k}{m}\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-45%282.61%29.png) |
(2.61) |
A partir de aquí, aplicando (2.57), se obtiene de forma inmediata la función de transferencia del modelo de estado:
![\[G\left( s \right) = \frac{{Y\left( s \right)}}{{U\left( s \right)}} = {\bf{C\Phi }}\left( s \right){\bf{B}} + {\bf{D}} = \left( {\begin{array}{*{20}{c}} 1 & 0 \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\frac{{s + \frac{\beta }{m}}}{{\Delta \left( s \right)}}} & {\frac{1}{{\Delta \left( s \right)}}} \\ { - \frac{k}{{m\Delta \left( s \right)}}} & {\frac{s}{{\Delta \left( s \right)}}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} 0 \\ {\frac{1}{m}} \\ \end{array}} \right) + 0 = \frac{{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-\nulldelimiterspace} m}}}{{\Delta \left( s \right)}} = \frac{{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-\nulldelimiterspace} m}}}{{{s^2} + \frac{\beta }{m}s + \frac{k}{m}}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-46%282.62%29.png) |
(2.62) |
Nótese que a este mismo resultado se podría haber llegado de forma directa, esto es, aplicando la transformada de Laplace y el concepto de función de transferencia sobre la ecuación diferencial (2.2) que caracteriza el comportamiento dinámico del sistema:
![\[m\ddot y\left( t \right) = u\left( t \right) - \beta \dot y\left( t \right) - ky\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-47%282.63%29.png) |
(2. 63) |
Aplicando la transformada de Laplace a la ecuación anterior con condiciones iniciales nulas:
![\[m{s^2}Y\left( s \right) = U\left( s \right) - \beta sY\left( s \right) - kY\left( s \right) \Rightarrow Y\left( s \right)\left( {{s^2} + \frac{\beta }{m}s + \frac{k}{m}} \right) = \frac{{U\left( s \right)}}{m} \Rightarrow G\left( s \right) = \frac{{Y\left( s \right)}}{{U\left( s \right)}} = \frac{{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-\nulldelimiterspace} m}}}{{{s^2} + \frac{\beta }{m}s + \frac{k}{m}}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-48%282.64%29.png) |
(2.64) |
Desde el punto de vista del modelo de estado, una vez que se ha obtenido éste interesa conocer la información que proporciona, esto es, la posibilidad de analizar el comportamiento dinámico del sistema a lo largo del tiempo. Para ello se debe tener una expresión explícita de la solución o trayectoria del sistema en su espacio de estado, esto es, del vector de estado. Esta solución exige el cálculo de la ecuación de estado. Cuando ésta es no lineal, su solución puede ser muy compleja, de modo que la mayoría de las veces habrá que descartar la obtención de una expresión analítica, quedando pues la solución en el ámbito del análisis numérico realizado mediante computador. Sin embargo, cuando la ecuación de estado es lineal, bien porque el sistema lo es, o bien porque es el resultado de la linealización de un sistema no lineal, la ecuación de estado admite una solución analítica que es fácil de obtener y proporciona una información muy rica de la evolución temporal de las trayectorias (coordenadas del vector de estado) del sistema.
Sea pues la ecuación de estado en su forma lineal siguiente:
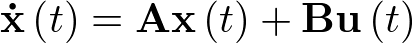 |
(2.65) |
Aplicando la transformada de Laplace con la condición inicial 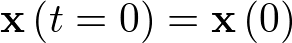 se tiene que
se tiene que
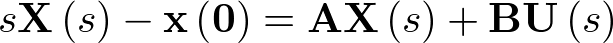 |
(2.66) |
O también
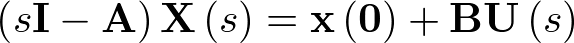 |
(2.67) |
Esto es,
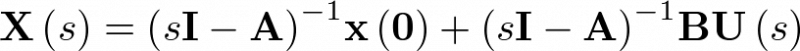 |
(2.68) |
Como se sabe, 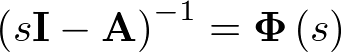 por tanto,
por tanto,
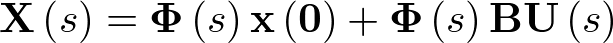 |
(2.69) |
Aplicando la transformada inversa de Laplace para obtener la solución temporal se tiene que
![${\bf{x}}\left( t \right) = {L^{\,\, - 1}}\left[ {{\bf{\Phi }}\left( s \right)} \right]\,{\bf{x}}\left( {\bf{0}} \right) + {L^{\,\, - 1}}\left[ {{\bf{\Phi }}\left( s \right){\bf{BU}}\left( s \right)} \right]$](/antonio.barragan/files/archivos_usuarios/78/form2.4-8%282.70%29.png) |
(2.70) |
La matriz
![${\bf{\Phi }}\left( t \right) = {L^{\,\, - 1}}\left[ {{\bf{\Phi }}\left( s \right)} \right]\,$](/antonio.barragan/files/archivos_usuarios/78/form2.4-9%282.71%29.png) |
(2.71) |
se denomina matriz de transición de estado. Nótese en la ecuación (2.70) como la matriz de transición de estado representa el paso del sistema desde el estado inicial 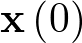 al considerado
al considerado 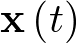 cuando la entrada es cero; esto es, describe la respuesta no forzada o natural del sistema.
cuando la entrada es cero; esto es, describe la respuesta no forzada o natural del sistema.
Teniendo en cuenta la operación de convolución16 en el dominio de la transformada de Laplace:
![$L\left[ {\int\limits_0^t {{f_1}\left( {t - \tau } \right){f_2}\left( \tau \right)d\tau } } \right] = {F_1}\left( s \right){F_2}\left( s \right);{\rm{ donde }}{F_1}\left( s \right) = L\left[ {{f_1}\left( t \right)} \right]{\rm{ y }}{F_2}\left( s \right) = L\left[ {{f_2}\left( t \right)} \right]$](/antonio.barragan/files/archivos_usuarios/78/form2.4-13%282.72%29.png) |
(2.72) |
Se tiene que la ecuación (2.70) puede ser escrita como
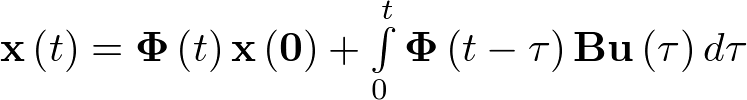 |
(2.73) |
Donde  representa un adelanto en el tiempo de valor
representa un adelanto en el tiempo de valor  de la función
de la función 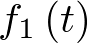 . La ecuación (2.73) es la solución de la ecuación diferencial de estado dada por (2.65). Evidentemente, si se conocen las condiciones iniciales
. La ecuación (2.73) es la solución de la ecuación diferencial de estado dada por (2.65). Evidentemente, si se conocen las condiciones iniciales 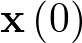 , la entrada
, la entrada 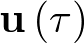 y la matriz de transición
y la matriz de transición 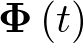 , puede calcularse numéricamente la solución de la ecuación de estado o respuesta temporal del vector de estado. Cuando el sistema no está forzado
, puede calcularse numéricamente la solución de la ecuación de estado o respuesta temporal del vector de estado. Cuando el sistema no está forzado 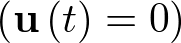 ésta es simplemente
ésta es simplemente
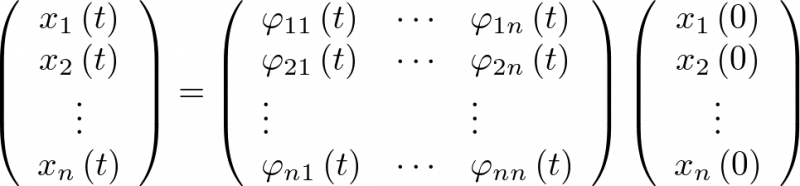 |
(2.74) |
Se puede comprobar fácilmente que la matriz de transición de estado  está dada por
está dada por
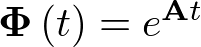 |
(2.75) |
Donde 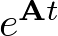 se denomina matriz exponencial. En efecto, supóngase que la entrada del sistema modelado por (2.65) es nula, con lo cual
se denomina matriz exponencial. En efecto, supóngase que la entrada del sistema modelado por (2.65) es nula, con lo cual
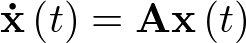 |
(2.76) |
Entonces, la solución de esta ecuación diferencial es, según (2.74),
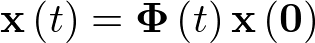 |
(2.77) |
Sustituyendo esta expresión en (2.76) se tiene que
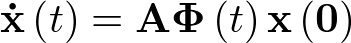 |
(2.78) |
Nótese que al derivar (2.77), el paso de esta ecuación a la (2.78) es inmediato si 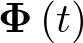 está dada por (2.75). Por tanto, la solución de la ecuación diferencial de estado puede ser escrita también como
está dada por (2.75). Por tanto, la solución de la ecuación diferencial de estado puede ser escrita también como
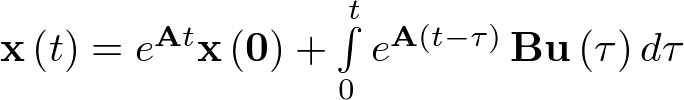 |
(2.79) |
Ejemplo 2.9. Respuesta temporal del sistema muelle – masa – amortiguador. Considérese que los valores de m, k y β del sistema de la figura 2.1 son tales que su ecuación de estado (2.7) está dada por
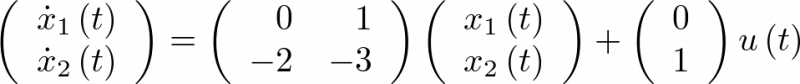 |
(2.80) |
Con objeto de evaluar la respuesta temporal del sistema se ha de calcular primero la matriz 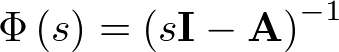 la cual se obtiene de la forma
la cual se obtiene de la forma
![\[\left( {s{\rm{I}} - {\rm{A}}} \right) = \left( {\left( {\begin{array}{*{20}{c}} s & 0 \\ 0 & s \\ \end{array}} \right) - \left( {\begin{array}{*{20}{c}} \hfill 0 & \hfill 1 \\ \hfill { - 2} & \hfill { - 3} \\ \end{array}} \right)} \right) = \left( {\begin{array}{*{20}{c}} s & { - 1} \\ 2 & {s + 3} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-34%282.81%29.png) |
(2.81) |
Por consiguiente,
![\[{\bf{\Phi }}\left( s \right) = {\left( {s{\rm{I}} - {\rm{A}}} \right)^{ - 1}} = \frac{1}{{\Delta \left( s \right)}}\left( {\begin{array}{*{20}{c}} {s + 3} & 1 \\ { - 2} & s \\ \end{array}} \right);{\rm{ donde }}\Delta \left( s \right) = \left| {\begin{array}{*{20}{c}} s & { - 1} \\ 2 & {s + 3} \\ \end{array}} \right| = {s^2} + 3s + 2 = \left( {s + 1} \right)\left( {s + 2} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-35%282.82%29.png) |
(2.82) |
Ahora, con objeto de obtener la descomposición en fracciones parciales se escribe
![\[{\bf{\Phi }}\left( s \right) = \left( {\begin{array}{*{20}{c}} {\frac{{s + 3}}{{\left( {s + 1} \right)\left( {s + 2} \right)}}} & {\frac{1}{{\left( {s + 1} \right)\left( {s + 2} \right)}}} \\ {\frac{{ - 2}}{{\left( {s + 1} \right)\left( {s + 2} \right)}}} & {\frac{s}{{\left( {s + 1} \right)\left( {s + 2} \right)}}} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\frac{A}{{s + 1}} + \frac{B}{{s + 2}}} & {\frac{C}{{s + 1}} + \frac{D}{{s + 2}}} \\ {\frac{E}{{s + 1}} + \frac{F}{{s + 2}}} & {\frac{G}{{s + 1}} + \frac{H}{{s + 2}}} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-36%282.83%29.png) |
(2.83) |
Operando como en el ejemplo 2.6 se tiene que
![\[{\bf{\Phi }}\left( s \right) = \left( {\begin{array}{*{20}{c}} {\frac{2}{{s + 1}} - \frac{1}{{s + 2}}} & {\frac{1}{{s + 1}} - \frac{1}{{s + 2}}} \\ { - \frac{2}{{s + 1}} + \frac{2}{{s + 2}}} & { - \frac{1}{{s + 1}} + \frac{2}{{s + 2}}} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-37%282.84%29.png) |
(2.84) |
Aplicando ahora la transformada inversa de Laplace,
![\[{\bf{\Phi }}\left( t \right) = {e^{{\bf{A}}t}} = {L^{\,\, - 1}}\left[ {{\bf{\Phi }}\left( s \right)} \right]\, = \left( {\begin{array}{*{20}{c}} {2{e^{ - t}} - {e^{ - 2t}}} & {{e^{ - t}} - {e^{ - 2t}}} \\ { - 2{e^{ - t}} + 2{e^{ - 2t}}} & { - {e^{ - t}} + 2{e^{ - 2t}}} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-38%282.85%29.png) |
(2.85) |
Una vez calculada la matriz de transición de estado, la respuesta temporal del sistema para diferentes condiciones iniciales y señales de entrada puede calcularse mediante la ecuación (2.73). Por ejemplo, cuando ![\[{x_1}\left( 0 \right) = {x_2}\left( 0 \right) = 1{\rm{ y }}u\left( t \right) = 0\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-39.png) se tiene que
se tiene que
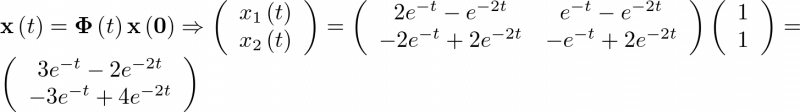 |
(2.86) |
El la figura 2.9 se muestra la evolución temporal del vector de estado para las condiciones iniciales dadas. Nótese que aunque la velocidad 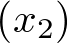 empieza a decrecer enseguida, hasta que no se hace cero, la masa (ver Figura 2.1) no para de moverse hacia abajo, con lo cual
empieza a decrecer enseguida, hasta que no se hace cero, la masa (ver Figura 2.1) no para de moverse hacia abajo, con lo cual 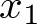 crece en este intervalo. En la Figura 2.10 se muestra la trayectoria del vector de estado en el espacio de estado del sistema (plano
crece en este intervalo. En la Figura 2.10 se muestra la trayectoria del vector de estado en el espacio de estado del sistema (plano 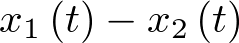 ). Esta representación se denomina retrato de fase. Nótese como el vector de estado, conforme el sistema va perdiendo la energía del estado inicial, tiende al punto (0,0) que es el punto de equilibrio o estado de mínima energía. El retrato de fase y el concepto de punto de equilibrio serán tratados en profundidad en el capítulo siguiente.
). Esta representación se denomina retrato de fase. Nótese como el vector de estado, conforme el sistema va perdiendo la energía del estado inicial, tiende al punto (0,0) que es el punto de equilibrio o estado de mínima energía. El retrato de fase y el concepto de punto de equilibrio serán tratados en profundidad en el capítulo siguiente.
 |
 |
Figura 2.9. Respuesta temporal de las variables de estado para ![\[{x_1}\left( 0 \right) = {x_2}\left( 0 \right) = 1{\rm{ y }}u\left( t \right) = 0.\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-44.png) |
|
 |
|
| Figura 2.10. Trayectoria del vector de estado en el espacio de estado | |
Considérese ahora que el sistema está forzado, esto es, 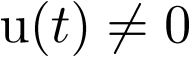 . Sea por ejemplo
. Sea por ejemplo 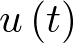 la función escalón unitario,
la función escalón unitario, 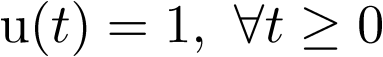 . En este caso, la ecuación (2.73) ha de ser usada en toda su extensión, utilizando el valor ya calculado de la matriz de transición
. En este caso, la ecuación (2.73) ha de ser usada en toda su extensión, utilizando el valor ya calculado de la matriz de transición 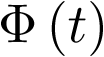 .
.
![\[{\bf{x}}\left( t \right) = \left( {\begin{array}{*{20}{c}} {2{e^{ - t}} - {e^{ - 2t}}} & {{e^{ - t}} - {e^{ - 2t}}} \\ { - 2{e^{ - t}} + 2{e^{ - 2t}}} & { - {e^{ - t}} + 2{e^{ - 2t}}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( 0 \right)} \\ {{x_2}\left( 0 \right)} \\ \end{array}} \right) + \int\limits_0^t {\,\left( {\begin{array}{*{20}{c}} {2{e^{ - \left( {t - \tau } \right)}} - {e^{ - 2\left( {t - \tau } \right)}}} & {{e^{ - \left( {t - \tau } \right)}} - {e^{ - 2\left( {t - \tau } \right)}}} \\ { - 2{e^{ - \left( {t - \tau } \right)}} + 2{e^{ - 2\left( {t - \tau } \right)}}} & { - {e^{ - \left( {t - \tau } \right)}} + 2{e^{ - 2\left( {t - \tau } \right)}}} \\ \end{array}} \right)} \left( {\begin{array}{*{20}{c}} 0 \\ 1 \\ \end{array}} \right)\left( 1 \right)d\tau \]](/antonio.barragan/files/archivos_usuarios/78/form2.4-51.png) |
(2.87) |
Después de operar con las matrices, el sumando que contiene la integral queda como
|
\[\begin{array}{l} \int\limits_0^t {\,\left( {\begin{array}{*{20}{c}} {{e^{ - \left( {t - \tau } \right)}} - {e^{ - 2\left( {t - \tau } \right)}}} \\ { - {e^{ - \left( {t - \tau } \right)}} + 2{e^{ - 2\left( {t - \tau } \right)}}} \\ \end{array}} \right)} d\tau = \left( {\begin{array}{*{20}{c}} {\int\limits_0^t {\left( {{e^{ - \left( {t - \tau } \right)}} - {e^{ - 2\left( {t - \tau } \right)}}} \right)} \,d\tau } \\ {\int\limits_0^t {\left( { - {e^{ - \left( {t - \tau } \right)}} + 2{e^{ - 2\left( {t - \tau } \right)}}} \right)} \,d\tau } \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{e^{ - t}}\int\limits_0^t {{e^\tau }d\tau - {e^{ - 2\tau }}\int\limits_0^t {{e^{2\tau }}d\tau } } } \\ { - {e^{ - t}}\int\limits_0^t {{e^\tau }d\tau + 2{e^{ - 2t}}\int\limits_0^t {{e^{2\tau }}d\tau } } } \\ \end{array}} \right) = \\ \left( {\begin{array}{*{20}{c}} {{e^{ - t}}\left[ {{e^\tau }} \right]_0^t - {\textstyle{1 \over 2}}{e^{ - 2\tau }}\left[ {{e^{2\tau }}} \right]_0^t} \\ { - {e^{ - t}}\left[ {{e^\tau }} \right]_0^t + {\textstyle{2 \over 2}}{e^{ - 2\tau }}\left[ {{e^{2\tau }}} \right]_0^t} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - {e^{ - t}} + {\textstyle{1 \over 2}}{e^{ - 2t}} + {\textstyle{1 \over 2}}} \\ {{e^{ - t}} - {e^{ - 2t}}} \\ \end{array}} \right) \\ \end{array}\] |
(2.88) |
 |
 |
Figura 2.11. Respuesta temporal de las variables de estado para ![\[{x_1}\left( 0 \right) = {x_2}\left( 0 \right) = 0{\rm{ y }}u\left( t \right) = 1\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-52-c.png) . . |
|
Con lo cual la ecuación (2.87) se escribirá de la forma
![\[\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {2{e^{ - t}} - {e^{ - 2t}}} & {{e^{ - t}} - {e^{ - 2t}}} \\ { - 2{e^{ - t}} + 2{e^{ - 2t}}} & { - {e^{ - t}} + 2{e^{ - 2t}}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( 0 \right)} \\ {{x_2}\left( 0 \right)} \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} { - {e^{ - t}} + {\textstyle{1 \over 2}}{e^{ - 2t}} + {\textstyle{1 \over 2}}} \\ {{e^{ - t}} - {e^{ - 2t}}} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-53%282.89%29.png) |
(2.89) |
La expresión anterior es la solución completa al comportamiento dinámico del sistema cuando la entrada es una señal escalón unitario. Por tanto, para conocer el estado del sistema en un instante de tiempo t, sólo hay que sustituir en la ecuación el valor de ese tiempo junto a las condiciones iniciales. Así por ejemplo, si el estado inicial es cero, la respuesta del sistema (trayectoria del vector de estado) es
![\[\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - {e^{ - t}} + {\textstyle{1 \over 2}}{e^{ - 2t}} + {\textstyle{1 \over 2}}} \\ {{e^{ - t}} - {e^{ - 2t}}} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-54%282.90%29.png) |
(2.90) |
El la figura 2.11 se muestra la evolución temporal del vector de estado según la ecuación (2.90). A modo de conclusión, en este ejemplo se ha mostrado como mediante la ecuación general (2.73), que implica el cálculo previo de la matriz de transición de estado17 [38], se puede calcular la respuesta temporal completa de un sistema (respuesta natural o no forzada más respuesta forzada) y, por ende, conocer su estado en cualquier instante t. Aunque su aplicación se limita a los sistemas lineales, esta metodología constituye una herramienta poderosa y fácil de escribir en forma de algoritmo para ser ejecutada en un computador.
En los sistemas de control de hoy en día el controlador suele ser un computador (ver Figura 1.1), con lo cual sus datos de entrada (y también de salida) son palabras digitales codificadas en binario. El circuito electrónico que presenta al computador una cadena de ceros y unos correspondientes al valor analógico de entrada convertido a digital es el convertidor analógico/digital (A/D); sin embargo, previo a él hay un circuito, integrado o no en el mismo convertidor, que se denomina muestreador y retenedor (sample & hold en inglés, S&H). La función del S&H es doble: 1) obtener muestras de la señal analógica cada cierto tiempo, normalmente constante, denominado periodo de muestreo T, y 2) mantener la señal muestreada constante el tiempo suficiente para que al convertidor A/D le dé tiempo a convertirla en una palabra digital.
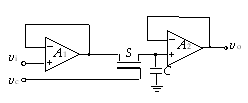 |
| Figura 2.12. Muestreador & retenedor. |
En la Figura 2.12 se muestra un esquema sencillo, casi conceptual, de S&H. Cuando una señal de control activa el interruptor S (un transistor MOSFET por ejemplo) el condensador C (un condensador de calidad para evitar fugas) se carga a la señal de entrada vi a través de la pequeña resistencia de entrada de A1 en configuración seguidor de tensión. Cuando la señal de control deja de estar activa, el interruptor se abre y la tensión almacenada en el condensador (señal muestreada) permanece estática, ya que la elevada resistencia de entrada de A2, también en configuración seguidor de tensión, evita su descarga. La tensión en el condensador es la de salida de A2, v0, y alimenta al convertidor A/D que iría a continuación. La señal de control del S&H debe ir ligada a la actuación del convertidor, con objeto de asegurar que éste tenga el tiempo suficiente para efectuar la conversión antes de capturar una nueva muestra. Nótese que el S&H funciona como una memoria analógica. En muestreo está memorizando la señal de entrada, mientras que en retención la recuerda y la mantiene en el tiempo.
En la Figura 2.13 se muestra de forma esquemática el efecto del muestreo sobre una señal continua 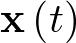 18 [39]. A partir de ésta, el circuito muestreador va obteniendo muestras
18 [39]. A partir de ésta, el circuito muestreador va obteniendo muestras ![\[x\left( 0 \right),x\left( 1 \right), \ldots ,x\left( n \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-57.png) cada incrementos de tiempo
cada incrementos de tiempo ![\[t\left( 0 \right),t\left( 1 \right), \ldots ,t\left( n \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.5-3.png) . El incremento de tiempo
. El incremento de tiempo 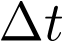 entre cada muestra es el tiempo o periodo de muestreo T, que normalmente es constante, con lo cual los intervalos temporales pueden ser escritos como
entre cada muestra es el tiempo o periodo de muestreo T, que normalmente es constante, con lo cual los intervalos temporales pueden ser escritos como 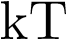 donde k es un índice entero de valor
donde k es un índice entero de valor ![\[k = 0,1,2, \ldots \]](/antonio.barragan/files/archivos_usuarios/78/form2.5-6.png)
 |
| Figura 2.13. Muestreo de una señal. |
El control por computador implica que las leyes de control se implementen mediante software19, con lo cual las acciones a realizar sobre un sistema bajo control se desarrollan en el computador mediante un algoritmo20 [40], el cual trabaja en tiempo discreto. Esto implica que el trabajo con el computador involucra el manejo de señales cuyo valor es aproximado, ya que no se tienen completas. Sin embargo, esto no quiere decir que a efectos prácticos se obtengan menos prestaciones, ya que el error, la mayoría de las veces, se puede acotar, con lo cual bastará con utilizar un periodo de muestreo más pequeño para obtener mayor precisión21 [41].
 |
| Figura 2.14. Definición de derivada. |
Ejemplo 2.10. Solución aproximada de una ecuación diferencial ordinaria. Considérese el cálculo numérico de una ecuación diferencial ordinaria de primer orden y sea ésta, como ejemplo, la siguiente:
| (2.91) |
La rama de las matemáticas que soluciona este tipo de problemas es el análisis o cálculo numérico. Esta disciplina crea algoritmos que permiten resolver problemas, en los que estén involucradas cantidades numéricas, con una precisión determinada.
El análisis numérico es de aplicación cuando: 1) Los problemas no tienen solución analítica o 2) el coste de cálculo de la solución analítica es mayor que la numérica. Para la resolución de ecuaciones diferenciales ordinarias los métodos más utilizados son el método de Euler y los métodos de Runge-Kutta22 [42].
Volviendo con el ejemplo, nótese en la Figura 2.14 que para T pequeño,  puede aproximarse por la relación incremental (definición de derivada) siguiente:
puede aproximarse por la relación incremental (definición de derivada) siguiente:
| (2.92) |
Resolviendo la ecuación anterior para 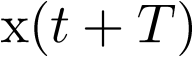 se tiene que
se tiene que
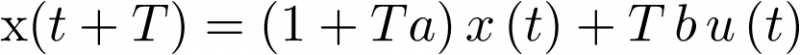 |
(2.93) |
Evaluando esta ecuación para un tiempo discreto cualquiera t = kT se obtiene la ecuación en diferencias siguiente:
![$x\left[ {\left( {k + 1} \right)T} \right] = \left( {1 + Ta} \right)x\left( {kT} \right) + T\,b\,u\left( {kT} \right)$](/antonio.barragan/files/archivos_usuarios/78/form2.5.1-5%282.94%29.png) |
(2.94) |
La cual, para un T dado, puede ser escrita como
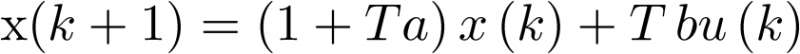 |
(2.95) |
La expresión anterior indica que el valor de la trayectoria (solución) en el instante de tiempo 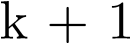 se calcula a partir del valor de x y de la excitación (entrada) u en el instante k.
se calcula a partir del valor de x y de la excitación (entrada) u en el instante k.
La ecuación diferencial original (2.91) ha sido pues transformada por este método numérico sencillo (denominado de Euler23 [43]) en la ecuación en diferencias (2.94). Ésta puede ser programada ahora mediante un algoritmo numérico simple en un computador. Así por ejemplo, si 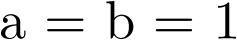 ,
,  y
y 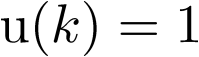 para k par;
para k par;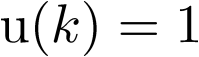 para k impar, y
para k impar, y 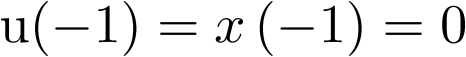 , se tiene que las primeras 5 muestras de
, se tiene que las primeras 5 muestras de 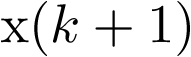 valen
valen
![\[\begin{array}{*{20}{c}} {x\left( 0 \right) = 2x\left( { - 1} \right) + u\left( { - 1} \right) = 0} \hfill \\ {x\left( 1 \right) = 2x\left( 0 \right) + u\left( 0 \right) = 0 + 1 = 1} \hfill \\ {x\left( 2 \right) = 2x\left( 1 \right) + u\left( 1 \right) = 2 + 0 = 2} \hfill \\ {x\left( 3 \right) = 2x\left( 2 \right) + u\left( 2 \right) = 4 + 1 = 5} \hfill \\ {x\left( 4 \right) = 2x\left( 3 \right) + u\left( 3 \right) = 10 + 0 = 10} \hfill \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.1-13.png) |
(2.96) |
Si se observa la ecuación (2.91), su expresión es la de un modelo de estado de orden 1 y, por ende, la ecuación (2.95) es la discretización de un modelo de estado de orden 1. Con objeto de extender lo anterior para el caso de sistemas de orden mayor que 1, se parte de la ecuación de estado lineal general que reproducimos a continuación por comodidad:
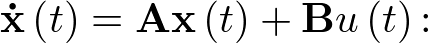 |
(2.97) |
Aplicando a esta ecuación el proceso descrito para llegar de (2.91) a (2.95), se tiene que la ecuación matricial en diferencias del modelo de estado lineal continuo estará dada por
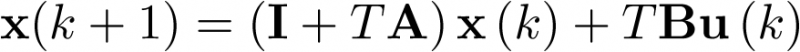 |
(2.98) |
Esta ecuación permite ver enseguida que la ecuación de estado discreta lineal tiene un aspecto muy similar a la de tiempo continuo. Ahora también dos matrices multiplican a los vectores de estado y de entrada igual que en el caso continuo. Respecto de la dependencia temporal de las variables, sus argumentos han sido sustituidos por el tiempo discreto k y por k + 1 para el vector de estado derivado. Esto se formalizará en la sección siguiente.
Ejemplo 2.11. Solución aproximada de un modelo de estado continuo de orden 2. Veamos una aplicación de la ecuación (2.98). Se van a calcular los primeros 4 valores discretos (iteraciones) del modelo continuo de ejemplo siguiente:
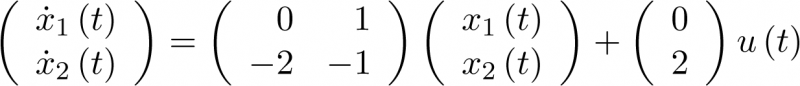 |
(2.99) |
Supóngase que T=0,02s, en cuyo caso la aplicación de la ecuación (2.98) sobre el ejemplo proporciona la expresión siguiente:
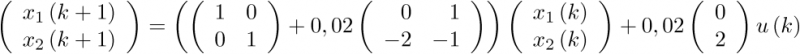 |
(2.100) |
Esto es,
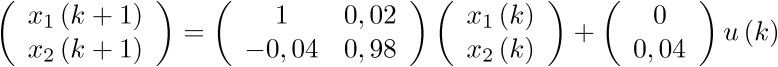 |
(2.101) |
Sea 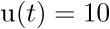 ,
,  , una señal escalón, con lo cual
, una señal escalón, con lo cual 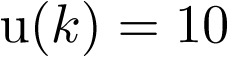 ,
, 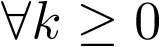 . Sea también
. Sea también 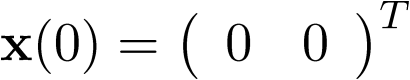 . Entonces,
. Entonces,
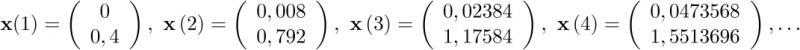 |
(2.102) |
Ejemplo 2.12. Respuesta temporal aproximada del sistema muelle – masa - amortiguador. En el ejemplo 2.9 se calculó la respuesta temporal exacta (analítica) de este sistema empleando la m-triz de transición de estado. Ahora se va a calcular de nuevo la respuesta temporal, pero mediante la aproximación en tiempo discreto.
El objetivo de este ejemplo es comparar la respuesta exacta del ejemplo 2.9 con la aproximada de éste; por ello es muy importante empezar a establecer una serie de pautas prácticas que permitirán obtener aproximaciones razonables.
La primera cuestión a considerar es qué periodo de muestreo elegir. Tal como se vio en la Figura 2.14, se ha de elegir un intervalo de tiempo T suficientemente pequeño de forma que la aproximación de derivada (ecuación 2.92) sea razonablemente precisa. Lógicamente, cada sistema tiene su propia dinámica y, en consecuencia, un periodo de muestreo que puede ser válido para un sistema no tiene porqué serlo para otro. Las Figuras 2.9 y 2.11 muestran la respuesta temporal del sistema objeto de análisis. Una observación mínima de las figuras no aconsejaría un tiempo de muestreo de por ejemplo T=0,2s; sin embargo, supóngase que el análisis no se ha realizado y se emplea este tiempo de muestreo, con lo cual la ecuación (2.97) es
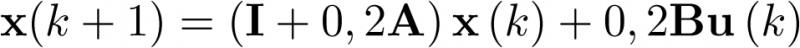 |
(2.103) |
Sustituyendo en esta ecuación los valores de las matrices A y B dadas en (2.80),
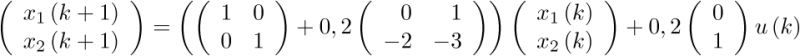 |
(2.104) |
Esto es,
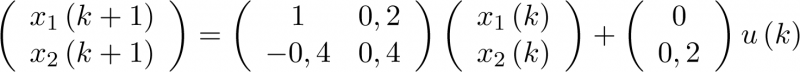 |
(2.105) |
Ahora, con objeto de comparar la respuesta aproximada en tiempo discreto con la exacta del ejemplo 2.9, considérese la aplicación de las mismas condiciones iniciales a la ecuación (2.105), ![\[{x_1}\left( 0 \right) = {x_2}\left( 0 \right) = 1\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.1-26.png) y
y ![\[u\left( t \right) = 0\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.1-27.png) , en cuyo caso la primera iteración proporciona el valor siguiente:
, en cuyo caso la primera iteración proporciona el valor siguiente:
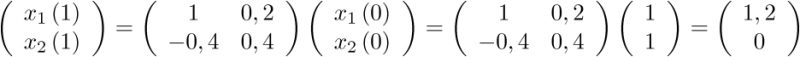 |
(2.106) |
Para las tres iteraciones siguientes se obtiene que
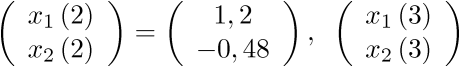 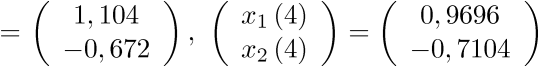 |
(2.107) |
El cálculo exacto para las 4 iteraciones: 0,2 s; 0,4 s; 0,6 s y 0,8 s; se realiza mediante la expresión (2.86):
| Tabla 2.1 | |||||||||
| Tiempo t | 0 | 0,2 | Error | 0,4 | Error | 0,6 | Error | 0,8 | Error |
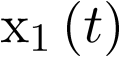 exacto exacto |
1 | 1,1156 | 7,56% | 1,1123 | 7,88% | 1,0440 | 14,94% | 0,9442 | 2,69% |
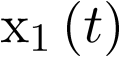 aprox., T=0,2s aprox., T=0,2s |
1 | 1,2 | 1,2 | 1,2 | 0.9696 | ||||
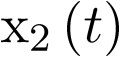 exacto exacto |
1 | 0,2251 | -100% | -0,2136 | -124,72% | -0,4417 | -52,14% | -0,5404 | -31,46% |
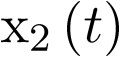 aprox., T=0,2s aprox., T=0,2s |
1 | 0 | -0,48 | -0,672 | -0,7104 | ||||
|
|
(2.108) |
En la tabla 2.1 se resumen los resultados obtenidos junto al error cometido. Como se puede comprobar, el error cometido en ![\[{x_2}\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.1-30b.png) es muy grande. Esto se comprende fácilmente observando la Figura 2.9, ya la pendiente negativa de
es muy grande. Esto se comprende fácilmente observando la Figura 2.9, ya la pendiente negativa de ![\[{x_2}\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.1-30b.png) al inicio es muy pronunciada, lo cual supone que su valor cambia mucho en 0,2 s.
al inicio es muy pronunciada, lo cual supone que su valor cambia mucho en 0,2 s.
Formalmente hablando, la frecuencia de muestreo24 [44] o inversa del periodo de muestreo, debe ser al menos el doble de la frecuencia más alta contenida en la señal analógica a muestrear. En la práctica es aconsejable que la frecuencia de muestreo esté comprendida entre 10 y 20 veces la de la frecuencia más alta contenida en la señal analógica a muestrear.
Si en vez del periodo de muestreo tomado se hubiera elegido uno 10 veces menor (frecuencia de muestreo 10 veces mayor), T=0,02s, el valor aproximado de ![\[{x_2}\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.1-30b.png) en la primera iteración por ejemplo, hubiera sido 0,9; y el real para t=0,02s, 0,9026. Esto es, dividiendo el periodo de muestreo por 10 el error pasa de -100% a -0,29%.
en la primera iteración por ejemplo, hubiera sido 0,9; y el real para t=0,02s, 0,9026. Esto es, dividiendo el periodo de muestreo por 10 el error pasa de -100% a -0,29%.
En los sistemas discretos 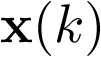 es una secuencia vectorial cuyo valor en cualquier punto de la secuencia es el estado del sistema en ese instante de tiempo discreto. También, al igual que en los sistemas continuos, el espacio de estado se define como el espacio vectorial donde toma valores el vector de estado
es una secuencia vectorial cuyo valor en cualquier punto de la secuencia es el estado del sistema en ese instante de tiempo discreto. También, al igual que en los sistemas continuos, el espacio de estado se define como el espacio vectorial donde toma valores el vector de estado 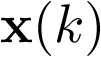 . De la misma forma, teniendo en cuenta que el estado se concreta como la mínima cantidad de información (mínimo conjunto de variables) precisa para conocer la evolución del sistema para todo kT, las variables de estado en tiempo discreto son también linealmente independientes, con lo cual la dimensión del espacio de estado coincide con el número de variables de estado.
. De la misma forma, teniendo en cuenta que el estado se concreta como la mínima cantidad de información (mínimo conjunto de variables) precisa para conocer la evolución del sistema para todo kT, las variables de estado en tiempo discreto son también linealmente independientes, con lo cual la dimensión del espacio de estado coincide con el número de variables de estado.
En virtud de lo anterior y por analogía con los sistemas continuos, se define como modelo de estado discreto de un sistema dinámico invariante con el tiempo, para un periodo de muestreo T dado, una relación matemática entre dos secuencias de entrada 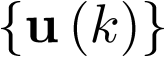 y salida
y salida 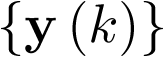 del modo siguiente:
del modo siguiente:
 |
(2.109) |
Donde la primera ecuación en  es la ecuación de estado, y la segunda en k es la de salida. La secuencia
es la ecuación de estado, y la segunda en k es la de salida. La secuencia 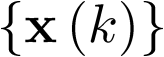 representa el vector de estado en tiempo discreto. Nótese por comparación de las ecuaciones (2.109) y (2.8) cómo para el caso discreto el modelo de estado se formula me-diante ecuaciones en diferencias, mientras que para el caso continuo se hace mediante ecuacio-nes diferenciales. Nótese también que si el sistema no fuera invariante con el tiempo (ver la primera sección del capítulo 3), las ecuaciones (2.107) deberían ser escritas como
representa el vector de estado en tiempo discreto. Nótese por comparación de las ecuaciones (2.109) y (2.8) cómo para el caso discreto el modelo de estado se formula me-diante ecuaciones en diferencias, mientras que para el caso continuo se hace mediante ecuacio-nes diferenciales. Nótese también que si el sistema no fuera invariante con el tiempo (ver la primera sección del capítulo 3), las ecuaciones (2.107) deberían ser escritas como 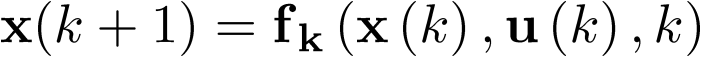 e
e 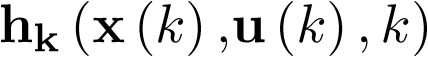 .
.
El concepto de linealidad en los sistemas discretos es análogo al de los sistemas continuos. Esto es, un modelo de estado discreto lineal e invariante con el tiempo puede ser escrito de la forma matricial siguiente:
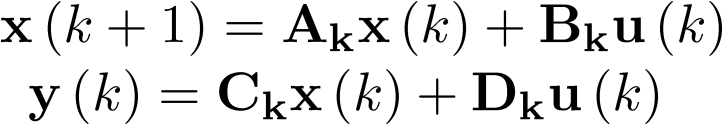 |
(2.110) |
Donde 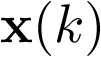 es el vector de estado en el instante k (de dimensión n),
es el vector de estado en el instante k (de dimensión n), 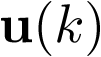 es el vector de entrada en el instante k (de dimensión p) e
es el vector de entrada en el instante k (de dimensión p) e 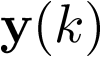 es el vector de salida en el instante k (de dimensión q). Ak, Bk, Ck y Dk son matrices constantes. La matriz Ak se denomina matriz de estado o matriz dinámica (de dimensión
es el vector de salida en el instante k (de dimensión q). Ak, Bk, Ck y Dk son matrices constantes. La matriz Ak se denomina matriz de estado o matriz dinámica (de dimensión 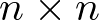 ), la matriz Bk se denomina matriz de entrada o matriz de control (de dimensión
), la matriz Bk se denomina matriz de entrada o matriz de control (de dimensión 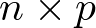 ), la matriz Ck se denomina matriz de salida o matriz sensora (de dimensión
), la matriz Ck se denomina matriz de salida o matriz sensora (de dimensión 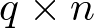 ), y la matriz Dk se denomina matriz de transferencia directa o simplemente término directo (de dimensión
), y la matriz Dk se denomina matriz de transferencia directa o simplemente término directo (de dimensión 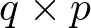 ).
).
Si bien la aproximación en tiempo discreto permite, como se ha visto, resolver (calcular la respuesta) sistemas lineales, éstos, la mayoría de las veces admiten solución analítica, que además es exacta. Sin embargo, los sistemas no lineales no admiten fácilmente una solución analítica, lo cual hace que su resolución se deba hacer de forma aproximada mediante métodos numéricos; en consecuencia, el método aproximado en tiempo discreto es particularmente útil para calcular la respuesta de sistemas no lineales.
Sea pues la expresión genérica de la ecuación de estado de un sistema invariante con el tiempo que puede ser no lineal:
![\[\frac{{d{\bf{x}}\left( t \right)}}{{dt}} = {\bf{f}}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right)} \right)\,\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-10%282.111%29.png) |
(2.111) |
Si se asume que respecto del vector de control el sistema es lineal, la ecuación anterior puede ser escrita como
![\[\frac{{d{\bf{x}}\left( t \right)}}{{dt}} = {\bf{f}}\left( {{\bf{x}}\left( t \right)} \right)\, + {\bf{Bu}}\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-11%282.112%29.png) |
(2.112) |
Utilizando la aproximación de derivada en tiempo discreto dada por (2.92).
![\[\frac{{{\bf{x}}\left( {t + T} \right) - {\bf{x}}\left( t \right)}}{T} = {\bf{f}}\left( {{\bf{x}}\left( t \right)} \right)\, + {\bf{Bu}}\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-12%282.113%29.png) |
(2.113) |
La ecuación anterior puede ser escrita en el instante k (para un periodo de muestreo T) de la forma
![\[\frac{{{\bf{x}}\left( {k + 1} \right) - {\bf{x}}\left( k \right)}}{T} = {\bf{f}}\left( {{\bf{x}}\left( k \right)} \right)\, + {\bf{Bu}}\left( k \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-13%282.114%29.png) |
(2.114) |
Con lo cual, resolviendo para ![\[{\bf{x}}\left( {k + 1} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-14.png) se tiene que
se tiene que
![\[{\bf{x}}\left( {k + 1} \right) = {\bf{x}}\left( k \right) + T\left( {{\bf{f}}\left( {{\bf{x}}\left( k \right)} \right)\, + {\bf{Bu}}\left( k \right)} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-15.png) |
(2.115) |
Ejemplo 2.13. Respuesta de un sistema no lineal. En el ejemplo 2.2 se dedujo un modelo lineal simple para describir la propagación de una enfermedad epidémica, el cual se reproduce a continuación por comodidad.
![\[\begin{array}{l} {{\dot x}_1}\left( t \right) = - \alpha {x_1}\left( t \right) - \beta {x_2}\left( t \right) + {u_1}\left( t \right) \\ {{\dot x}_2}\left( t \right) = \lambda {x_1}\left( t \right) - \gamma {x_2}\left( t \right) + {u_2}\left( t \right) \\ {{\dot x}_3}\left( t \right) = \alpha {x_1}\left( t \right) + \gamma {x_2}\left( t \right) \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-16%282.116%29.png) |
(2.116) |
El precio que se pagó entonces para hacer lineal el modelo y poderlo tratar en forma matricial, fue el no tener en cuenta la interacción entre las variables población en riesgo de ser infectada 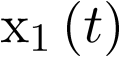 y población infectada
y población infectada 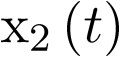 . Ahora se va a mejorar el modelo teniendo en cuenta esta interacción del modo siguiente:
. Ahora se va a mejorar el modelo teniendo en cuenta esta interacción del modo siguiente:
![\[\begin{array}{l} {{\dot x}_1}\left( t \right) = - \alpha {x_1}\left( t \right) - \beta {x_1}\left( t \right){x_2}\left( t \right) + {u_1}\left( t \right) \\ {{\dot x}_2}\left( t \right) = \beta {x_1}\left( t \right){x_2}\left( t \right) - \gamma {x_2}\left( t \right) + {u_2}\left( t \right) \\ {{\dot x}_3}\left( t \right) = \alpha {x_1}\left( t \right) + \gamma {x_2}\left( t \right) \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-17%282.117%29.png) |
(2.117) |
El modelo (2.116) es no lineal, por tanto no admite un tratamiento matricial como en el Ejemplo 2.12. Sean los parámetros 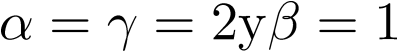 , con lo cual empleando la ecuación (2.115), el modelo (2.117) se escribirá en modo discreto de la forma
, con lo cual empleando la ecuación (2.115), el modelo (2.117) se escribirá en modo discreto de la forma
![\[\begin{array}{l} {x_1}\left( {k + 1} \right) = {x_1}\left( k \right) + T\left( { - 2{x_1}\left( k \right) - {x_1}\left( k \right){x_2}\left( k \right) + {u_1}\left( k \right)} \right) \\ {x_2}\left( {k + 1} \right) = {x_2}\left( k \right) + T\left( {{x_1}\left( k \right){x_2}\left( k \right) - 2{x_2}\left( k \right) + {u_2}\left( k \right)} \right) \\ {x_3}\left( {k + 1} \right) = {x_3}\left( k \right) + 2T\left( {{x_1}\left( k \right) + {x_2}\left( k \right)} \right) \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-19%282.118%29.png) |
(2.118) |
Sean las condiciones iniciales 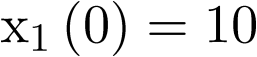 ,
,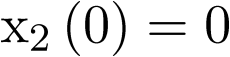 y
y ![\[{x_3}\left( 0 \right) = 0\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-22.png) . Nótese que en un caso real, el valor de estas variables podría estar en cientos o miles de individuos. Del mismo modo, la medida de tiempo podría ser días o meses. Considérese ahora que en el instante inicial hay aporte de individuos a la población infectada, el cual representaremos como
. Nótese que en un caso real, el valor de estas variables podría estar en cientos o miles de individuos. Del mismo modo, la medida de tiempo podría ser días o meses. Considérese ahora que en el instante inicial hay aporte de individuos a la población infectada, el cual representaremos como ![\[{u_2}\left( 0 \right) = 1\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-23.png) (recuérdese que el significado físico de las entradas es velocidad de aporte), pero no hay aporte a la población en riesgo, con lo cual
(recuérdese que el significado físico de las entradas es velocidad de aporte), pero no hay aporte a la población en riesgo, con lo cual 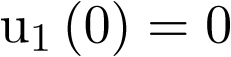 . Por último, asúmase que
. Por último, asúmase que ![\[{u_1}\left( k \right) = 0\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-25.png) ,
,![\[\forall k > 0\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-26.png) y que la entrada
y que la entrada 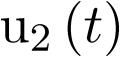 decae con el tiempo hasta anularse del modo siguiente:
decae con el tiempo hasta anularse del modo siguiente: ![\[{u_2}\left( 1 \right) = 0,5\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-28.png) ; y
; y ![\[{u_2}\left( k \right) = 0\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-29.png) ,
, ![\[\forall k > 1\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-30.png) . Teniendo en cuenta pues las condiciones establecidas, la expresión general del modelo en tiempo discreto para T = 0,1 será
. Teniendo en cuenta pues las condiciones establecidas, la expresión general del modelo en tiempo discreto para T = 0,1 será
![\[\begin{array}{l} {x_1}\left( {k + 1} \right) = 0,8\,{x_1}\left( k \right) - 0,1\,{x_1}\left( k \right){x_2}\left( k \right) \\ {x_2}\left( {k + 1} \right) = 0,8\,{x_2}\left( k \right) + 0,1\,{x_1}\left( k \right){x_2}\left( k \right) + 0,1\,{u_2}\left( k \right) \\ {x_3}\left( {k + 1} \right) = {x_3}\left( k \right) + 0,2\,{x_1}\left( k \right) + 0,2\,{x_2}\left( k \right) \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.5.2-31%282.119%29.png) |
(2.119) |
A partir de aquí y de modo iterativo se calcula la respuesta para cada instante de tiempo discreto k.
| (2.120) |
El análisis de los sistemas lineales discretos se ve facilitado por el uso de una herramienta matemática denominada transformada ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) , la cual se define a partir de una secuencia de números
, la cual se define a partir de una secuencia de números 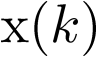 del modo siguiente:
del modo siguiente:
![${\rm{Z}}\left[ {x\left( k \right)} \right] = X\left( z \right) = \sum\limits_{k = 0}^\infty {x\left( k \right)} \,{z^{ - k}}$](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-3%282.121%29.png) |
(2.121) |
La ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) transformada definida por la ecuación anterior se denomina unilateral, ya que se considera que
transformada definida por la ecuación anterior se denomina unilateral, ya que se considera que 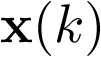 sólo está definido para
sólo está definido para 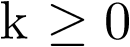 ; para el caso que esté definido desde
; para el caso que esté definido desde  , se sustituye el índice inferior de la sumatoria de (2.120) por este valor y la transformada
, se sustituye el índice inferior de la sumatoria de (2.120) por este valor y la transformada ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) es denominada bilateral. La transformada
es denominada bilateral. La transformada ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) de aplicación a sistemas de tiempo discreto guarda una gran anlogía con la transformada de Laplace de aplicación a los sistemas de tiempo continuo. Así, para condiciones iniciales nulas,
de aplicación a sistemas de tiempo discreto guarda una gran anlogía con la transformada de Laplace de aplicación a los sistemas de tiempo continuo. Así, para condiciones iniciales nulas,
![$L\left[ {{\bf{\dot x}}\left( t \right)} \right] = s\,L\left[ {{\bf{x}}\left( t \right)} \right] \Rightarrow {\rm{Z}}\left[ {{\bf{x}}\left( {k + 1} \right)} \right] = z\,{\rm{Z}}\left[ {{\bf{x}}\left( k \right)} \right]$](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-6%282.122%29.png) |
(2.122) |
Teniendo en cuenta esta correspondencia entre sistemas continuos y discretos, se pueden volver a plantear para éstos las mismas metodologías que se aplicaron a los sistemas en tiempo continuo. En concreto: 1) el concepto de función de transferencia discreta por analogía con la función de transferencia continua; 2) la solución de ecuaciones en diferencias por analogía con la solución de ecuaciones diferenciales, y 3) la obtención de la función de transferencia discreta a partir del modelo de estado discreto sin más que cambiar s por z.
En virtud de lo anterior, la función de transferencia de un sistema lineal e invariante en tiempo discreto se define como la relación entre la transformada ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) de la variable de salida y la transformada
de la variable de salida y la transformada ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) de la variable de entrada, suponiendo que todas las condiciones iniciales se hacen iguales a cero. Así, dado el sistema de la Figura 2.15, su función de transferencia será:
de la variable de entrada, suponiendo que todas las condiciones iniciales se hacen iguales a cero. Así, dado el sistema de la Figura 2.15, su función de transferencia será:
 |
| Figura 2.15. Sistema de una entrada – una salida (SISO). |
![$F\left( z \right) = {\left. {\frac{{Z\left[ {y\left( k \right)} \right]}}{{Z\left[ {u\left( k \right)} \right]}}} \right|_{\scriptstyle {\rm{Cond}}{\rm{. iniciales}} \hfill \atop \scriptstyle {\rm{nulas}} \hfill}} = \frac{{Y\left( z \right)}}{{X\left( z \right)}}$](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-8%282.123%29.png) |
(2.123) |
Aplicando la ecuación de definición de transformada ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) a las señales de interés, se obtiene la expresión en el dominio z de dichas señales. Así por ejemplo, para el caso de la señal escalón unitario
a las señales de interés, se obtiene la expresión en el dominio z de dichas señales. Así por ejemplo, para el caso de la señal escalón unitario 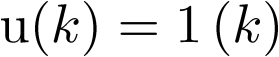 ,
,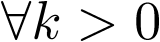 , se tendrá que aplicando (2.120),
, se tendrá que aplicando (2.120),
![$U\left( z \right) = Z\left[ {1\left( k \right)} \right] = \sum\limits_{k = 0}^\infty {1\,{z^{ - k}}} = \sum\limits_{k = 0}^\infty {{z^{ - k}} = 1 + } {z^{ - 1}} + {z^{ - 2}} + \cdots $](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-11%282.124%29.png) |
(2.124) |
Utilizando la identidad
| (2.125) |
Se tiene para 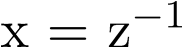 que la ecuación (2.124) puede ser escrita como
que la ecuación (2.124) puede ser escrita como
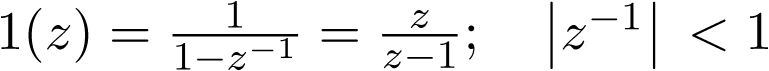 |
(2.126) |
Al igual que ocurría en el caso de la transformada de Laplace, existen tablas25 [45] de pares de transformadas 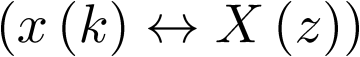 que evitan el tedio de tener que aplicar cada vez la expresión (2.126).
que evitan el tedio de tener que aplicar cada vez la expresión (2.126).
Ejemplo 2.14. Función de transferencia de un sistema definido por una ecuación en diferencias. Sea el sistema definido por la ecuación en diferencias siguiente:
 |
(2.127) |
Del mismo modo que en el paso del tiempo continuo al dominio de la transformada de Laplace se aplicó la propiedad de diferenciación real (expresiones (2.40) a (2.41)), ahora, para pasar del tiempo discreto al dominio de la transformada  se aplica la propiedad de traslación real en el tiempo:
se aplica la propiedad de traslación real en el tiempo:
|
|
(2.128) |
Esto permite transformar la ecuación en diferencias (2.126) en la expresión
![\[X\left( z \right) + 3{z^{ - 1}}X\left( z \right) + 3{z^{ - 2}}X\left( z \right) + {z^{ - 3}}X\left( z \right) = {z^{ - 2}}U\left( z \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-17%281.129%29.png) |
(2.129) |
De aquí,
![\[\frac{{X\left( z \right)}}{{U\left( z \right)}} = \frac{{{z^{ - 2}}}}{{1 + 3{z^{ - 1}} + 3{z^{ - 2}} + {z^{ - 3}}}} = \frac{z}{{{z^3} + 3{z^2} + 3z + 1}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-18%281.130%29.png) |
(2.130) |
Ejemplo 2.15. Resolución de una ecuación en diferencias. Igual que la transformada de Laplace es una herramienta útil para resolver ecuaciones diferenciales lineales, la transformada  lo es para resolver ecuaciones en diferencias lineales. Dada pues la ecuación en diferencias (2.130), se trata de obtener la solución
lo es para resolver ecuaciones en diferencias lineales. Dada pues la ecuación en diferencias (2.130), se trata de obtener la solución 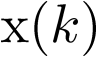 para las condiciones:
para las condiciones: ![\[u\left( 0 \right) = u\left( 1 \right) = 1\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-19.png) ;
; 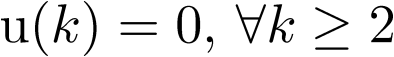 y
y 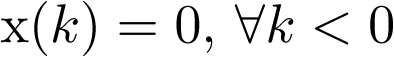 .
.
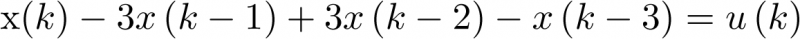 |
(2.131) |
La transformada  del primer miembro de la ecuación anterior se obtiene como en el ejemplo precedente. Respecto de la transformada
del primer miembro de la ecuación anterior se obtiene como en el ejemplo precedente. Respecto de la transformada  de la entrada, aplicando la definición de transformada
de la entrada, aplicando la definición de transformada  , (2.120):
, (2.120):
![\[Z\left[ {u\left( k \right)} \right] = U\left( z \right) = \sum\limits_{k = 0}^\infty {u\left( k \right)} \,{z^{ - k}} = u\left( 0 \right){z^0} + u\left( 1 \right){z^{ - 1}} + u\left( 2 \right){z^{ - 2}} + \cdots = 1 + {z^{ - 1}} = \frac{{z + 1}}{z}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-23%282.132%29.png) |
(2.132) |
La transformada ![\[Z\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) de (2.130) puede ser ya escrita como
de (2.130) puede ser ya escrita como
![\[X\left( z \right)\left[ {1 - 3{z^{ - 1}} + 3{z^{ - 2}} - {z^{ - 3}}} \right] = \frac{{z + 1}}{z} \Rightarrow \frac{{X\left( z \right)}}{z} = \frac{{{z^2} + z}}{{{z^3} - 3{z^2} + 3z - 1}} = \frac{{{z^2} + z}}{{{{\left( {z - 1} \right)}^3}}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-24%282.133%29.png) |
(2.133) |
Un poco más adelante se verá por qué interesa despejar la variable a calcular dividida por z. Ahora, al igual que se procedía para la transformada de Laplace, se descompone la relación de polinomios en fracciones simples. Nótese que la raíz del denominador (polo) es de multiplicidad 3.
![\[\frac{{X\left( z \right)}}{z} = \frac{{{z^2} + z}}{{{{\left( {z - 1} \right)}^3}}} = \frac{A}{{z - 1}} + \frac{B}{{{{\left( {z - 1} \right)}^2}}} + \frac{C}{{{{\left( {z - 1} \right)}^3}}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-25%282.134%29.png) |
(2.134) |
Para el cálculo de C se puede proceder como en el caso cuando no hay polos múltiples, esto es, multiplicando ambos miembros de esta última ecuación por 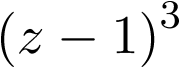 se tiene que
se tiene que
![\[{\left( {z - 1} \right)^3}\frac{{{z^2} + z}}{{{{\left( {z - 1} \right)}^3}}} = A{\left( {z - 1} \right)^2} + B\left( {z - 1} \right) + C\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-27%282.135%29.png) |
(2.135) |
A partir de aquí basta con sustituir el valor del polo para calcular C:
![\[C = {\left. {{z^2} + z} \right|_{z = 1}} = 2\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-28%282.136%29.png) |
(2.136) |
El resto de términos no pueden ser calculados de la misma forma. Una opción que dependiendo del caso puede ser algo tediosa, es sustituir el valor calculado de C en (2.134) e identificar los términos en las potencias de z:
![\[{z^2} + z = A{\left( {z - 1} \right)^2} + B\left( {z - 1} \right) + 2 = A{z^2} - 2Az + A + Bz - B + 2\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-29%282.137%29.png) |
(2.137) |
Del término en 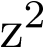 se deduce que A=1. Del término independiente,
se deduce que A=1. Del término independiente, 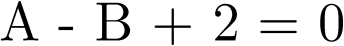 , se deduce que B=3 Al mismo resultado podríamos haber llegado de una forma más sistemática elimi-nando de forma sucesiva el índice de multiplicidad del polo, esto es, derivando cada vez respecto de z ambos miembros de (2.136):
, se deduce que B=3 Al mismo resultado podríamos haber llegado de una forma más sistemática elimi-nando de forma sucesiva el índice de multiplicidad del polo, esto es, derivando cada vez respecto de z ambos miembros de (2.136):
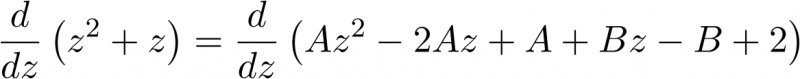 |
(2.138) |
Esto es,
![\[2z + 1 = 2A\left( {z - 1} \right) + B\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-33%282.139%29.png) |
(2.139) |
Sustituyendo en la ecuación anterior el valor del polo z=1 se tiene de nuevo que B=3 Por último, derivando ahora (2.138) respecto de z se obtiene que A=1.
En definitiva, la expresión (2.133) puede ser escrita en forma de fracciones simples del modo siguiente:
![\[\frac{{X\left( z \right)}}{z} = \frac{1}{{z - 1}} + \frac{3}{{{{\left( {z - 1} \right)}^2}}} + \frac{2}{{{{\left( {z - 1} \right)}^3}}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-34%282.140%29.png) |
(2.140) |
A partir de aquí se escribe la expresión anterior en la forma como aparecen los términos en las tablas de transformadas, esto es, en potencias de z-1,
 |
(2.141) |
Aplicando la transformada z inversa26 [46], z-1, a la ecuación anterior sabiendo que
![\[Z\left[ {1\left( k \right)} \right] = \frac{1}{{1 - {z^{ - 1}}}}{\rm{, }}Z\left[ {kT} \right]{\rm{ = }}\frac{{T{z^{ - 1}}}}{{{{\left( {1 - {z^{ - 1}}} \right)}^2}}}{\rm{ y }}Z\left[ {\frac{{k\left( {k - 1} \right) \cdots \left( {k - m + 2} \right)}}{{\left( {m - 1} \right){\rm{!}}}}} \right] = \frac{{{z^{ - m + 1}}}}{{{{\left( {1 - {z^{ - 1}}} \right)}^m}}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-36%282.142%29.png) |
(2.142) |
Se obtiene la solución de (2.126):
![\[x\left( k \right) = 1\left( k \right) + 3k + 2\frac{{k\left( {k - 1} \right)}}{{2{\rm{!}}}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-37%282.143%29.png) |
(2.143) |
Para los primeros 3 muestreos se tiene que
![\[\begin{array}{*{20}{c}} {x\left( 0 \right) = 1\left( 0 \right) = 1} \hfill \\ {x\left( 1 \right) = 1\left( 1 \right) + 3\,.1 = 4} \hfill \\ {x\left( 2 \right) = 1\left( 2 \right) + 3\,.\,2\, + 2\frac{{2\,.1}}{{2{\rm{!}}}} = 9} \hfill \\ {x\left( 3 \right) = 1\left( 3 \right) + 3\,.\,3\, + 2\frac{{3\,.\,2}}{{2{\rm{!}}}} = 16} \hfill \\ \end{array}\,\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-38%282.144%29.png) |
(2.144) |
La ecuación en diferencias (2.126) podría haber sido resuelta también de forma iterativa como en el ejemplo 2.10, esto es:
![\[\begin{array}{*{20}{c}} {x\left( 0 \right) = u\left( 0 \right) = 1} \hfill \\ {x\left( 1 \right) = u\left( 1 \right) + 3x\left( 0 \right) = 4} \hfill \\ {x\left( 2 \right) = 3x\left( 1 \right) - 3x\left( 0 \right) = 9} \hfill \\ {x\left( 3 \right) = 3x\left( 2 \right) - 3x\left( 1 \right) + x\left( 0 \right) = 16} \hfill \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-39%282.145%29.png) |
(2.145) |
Obtención de la función de transferencia a partir del modelo de estado
Vamos a ver a continuación como la forma de obtener la función de transferencia discreta de un sistema de una única entrada y una única salida (SISO), definido por su modelo discreto de estado, es análoga al caso continuo. Sea pues el modelo discreto de estado:
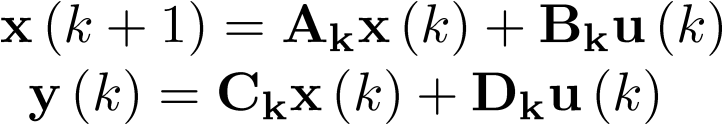 |
(2.146) |
Aplicando la transformada z (2.121) a la ecuación de estado y a la ecuación de salida anteriores, se tiene que
![\[\begin{array}{l} z{\bf{X}}\left( z \right) = {\bf{AX}}\left( z \right) + {\bf{B}}U\left( z \right) \\ Y\left( z \right) = {\bf{CX}}\left( z \right) + {\bf{D}}U\left( z \right) \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-41%282.147%29.png) |
(2.147) |
Donde B es una matriz de orden nx1 debido a que el sistema tiene una única entrada u. Obsérvese que no se tienen en cuenta las condiciones iniciales, ya que lo que se busca es una función de transferencia. A partir de aquí, procediendo de forma análoga al caso continuo (ecuaciones (2.54) a (2.56)), se llega a la expresión que permite obtener de forma directa la función de transferencia de un modelo de estado discreto lineal de una entrada y una salida (SISO).
![\[G\left( z \right) = {{\bf{C}}_{\bf{k}}}{\bf{\Phi }}\left( z \right){{\bf{B}}_{\bf{k}}} + {{\bf{D}}_{\bf{k}}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-42%282.148%29.png) |
(2.148) |
Donde
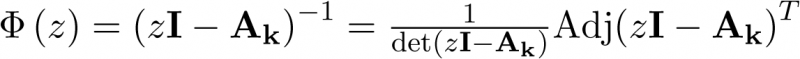 |
(2.149) |
De nuevo, como en el caso continuo, queda claro que el polinomio denominador de la función de transferencia es 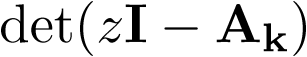 . Esto es, los polos del sistema coinciden con los valores propios o autovalores de la matriz Ak. En conclusión, los polos del sistema dependen sólo de la matriz Ak, mientras que los ceros dependen de las matrices Ak, Bk, Ck y Dk.
. Esto es, los polos del sistema coinciden con los valores propios o autovalores de la matriz Ak. En conclusión, los polos del sistema dependen sólo de la matriz Ak, mientras que los ceros dependen de las matrices Ak, Bk, Ck y Dk.
Dada una función f, se dice que es lineal si cumple que ![\[\left. 1 \right)f\left( {u,v} \right) = f\left( u \right) + f\left( v \right){\rm{ y }}\left. 2 \right)f\left( {ku} \right) = kf\left( u \right),\]](/antonio.barragan/files/archivos_usuarios/78/form2.1-12.png) donde k es un escalar.
donde k es un escalar.
El matemático y físico Joseph Louis Lagrange (1736–1813), dijo que Newton fue el más grande genio que ha existido y también el más afortunado dado que sólo se puede encontrar una vez un sistema que rija el mundo.
Para muchos y aunque de muy difícil lectura, la obra más importante que registra hasta ahora la historia de la ciencia.
Quizás el único fallo que tenía la teoría de Newton (y él era consciente de ello) era que las fuerzas que se ejercían entre los cuerpos a distancia operaban de forma instantánea. Aún así, las ideas newtonianas fueron parte del programa de todo investigador en el campo de la física teórica hasta finales del siglo XIX. No fue hasta la teoría del campo electromagnético promulgada por Maxwell cuando se comprendió con claridad que las interacciones eléctricas y magnéticas entre los cuerpos no eran debidas a fuerzas que operaran de modo instantáneo y a distancia, sino a procesos que se propagaban a través del espacio a una velocidad finita. El terreno estaba ya preparado y las aportaciones de Mach, Poincaré y Lorentz, desembocaron en la Teoría de la Relatividad Restringida de Albert Einstein en la que, al abandonarse la noción de absoluta simultaneidad se excluía la existencia de fuerzas que actúan instantáneamente a dis-tancia. El espacio y también el tiempo, quedaban despojados de su capacidad causal absoluta y pasaron a ser entes afectados por las masas del Universo en estrecha relación, ahora, con la energía. La teoría General de la Relatividad, la nueva teoría de la gravitación, sustituiría a la gravitación newtoniana. Las leyes del movimiento de Newton sólo son válidas para pequeñas distancias, las del sistema solar, y para pequeñas velocidades, que ahora también tienen un límite, el de la velocidad de la luz.
Un sistema puede tener más de una entrada; imagínese por ejemplo un barco con más de un motor actuando a la vez para moverlo.
Para un modelo no lineal siempre se podrá linealizar en torno al punto de operación.
Para un sistema variante con el tiempo se escribiría 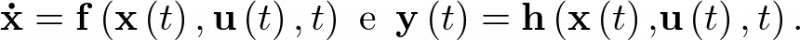
Para el caso general de una función de n variables  su desarrollo en serie de Taylor puede encontrarse en textos matemáticos y direcciones de Internet. Véase por ejemplo: http://es.wikipedia.org/wiki/Serie_de_Taylor [47]
su desarrollo en serie de Taylor puede encontrarse en textos matemáticos y direcciones de Internet. Véase por ejemplo: http://es.wikipedia.org/wiki/Serie_de_Taylor [47]
Pierre-Simon Laplace (Beaumont-en-Auge (Normandía); 23 de marzo de 1749 - París; 5 de marzo de 1827) astrónomo, físico y matemático francés que inventó y desarrolló, entre otras cosas, la transformada de Laplace. La Transformada de Laplace de una función f(t) para todos los números reales t ≥ 0, es la función definida por:  . Donde s es una variable compleja y
. Donde s es una variable compleja y  . Esta transformada integral tiene una serie de propiedades que la hacen útil en el análisis de sistemas lineales. Una de las ventajas más significativas radica en que la integración y derivación se convierten en multiplicación y división. Esto transforma las ecuaciones diferenciales e integrales en ecuaciones polinómicas, mucho más fáciles de resolver. El modo de operar consiste en transformar por la integral la función f(t) en la función F(s), para lo cual en la práctica se utilizan tablas de transformadas. Éstas pueden ser encontradas en textos y direcciones de Internet. Véase por ejemplo: http://es.wikipedia.org/wiki/Transformada_de_Laplace [48].
. Esta transformada integral tiene una serie de propiedades que la hacen útil en el análisis de sistemas lineales. Una de las ventajas más significativas radica en que la integración y derivación se convierten en multiplicación y división. Esto transforma las ecuaciones diferenciales e integrales en ecuaciones polinómicas, mucho más fáciles de resolver. El modo de operar consiste en transformar por la integral la función f(t) en la función F(s), para lo cual en la práctica se utilizan tablas de transformadas. Éstas pueden ser encontradas en textos y direcciones de Internet. Véase por ejemplo: http://es.wikipedia.org/wiki/Transformada_de_Laplace [48].
La transformada inversa de Laplace 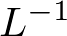 permite encontrar la función del tiempo f(t) a partir de la transformada de Laplace F(s):
permite encontrar la función del tiempo f(t) a partir de la transformada de Laplace F(s): ![${L^{ - 1}}\left[ {F\left( s \right)} \right] = \int_{\sigma - j\infty }^{\sigma + j\infty } {F\left( s \right){e^{st}}} ds,{\rm{ para }}t > 0$](/antonio.barragan/files/archivos_usuarios/78/form2.3-8_0.png) Donde
Donde  es una constante real.
es una constante real.
La instrucción de MATLAB laplace devuelve la función de s correspondiente a una función de t.
Para el caso de que la expresión a desarrollar contenga polos múltiples del tipo 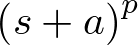 ver ejemplo 2.15. El caso general puede ser consultado en textos y direcciones de Internet. Véase por ejemplo: http://www.scribd.com/doc/6075394/DescomposiciOn-Fracciones-Parciales [49]. La función de MATLAB residue realiza la expansión en fracciones parciales de la relación de dos polinomios B(s)/A(s).
ver ejemplo 2.15. El caso general puede ser consultado en textos y direcciones de Internet. Véase por ejemplo: http://www.scribd.com/doc/6075394/DescomposiciOn-Fracciones-Parciales [49]. La función de MATLAB residue realiza la expansión en fracciones parciales de la relación de dos polinomios B(s)/A(s).
La función de MATLAB ilaplace calcula la transformada inversa de Laplace.
Raíces del polinomio denominador de la función de transferencia.
Raíces del polinomio numerador de la función de transferencia.
La operación matemática 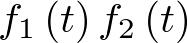 se denomina convolución
se denomina convolución
Salvo para cálculos sencillos de lápiz y papel, la matriz de transición de estado no se suele calcular por el procedimiento de este ejemplo, esto es, invirtiendo la matriz ![\[\left( {s{\bf{I}} - {\bf{A}}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.3-33.png) para pasar después al dominio del tiempo. Existen métodos analíticos, como el de interpolación de Sylvester por ejemplo, que permiten calcular la matriz de transición de estado en su forma exponencial
para pasar después al dominio del tiempo. Existen métodos analíticos, como el de interpolación de Sylvester por ejemplo, que permiten calcular la matriz de transición de estado en su forma exponencial 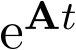 de modo directo.
de modo directo.
El proceso de conversión A/D tiene tres etapas perfectamente diferenciadas, a saber: muestreo, cuantificación y codificación. Nótese que la señal muestreada no contiene errores para los instantes de muestreo, ya que en ellos el valor capturado es análogo al de la señal original. Sin embargo, el proceso siguiente al muestreo, cuantificación, atribuye un valor finito (discreto) de amplitud a la señal muestreada, seleccionado por aproximación dentro de un margen de niveles previamente fijado, lo cual introduce en el proceso un error denominado error de cuantificación. Por último, la etapa de codificación traduce el valor finito cuantificado en una sucesión de ceros y unos que corresponde al valor binario de la señal muestreada. Esta palabra digital correspondiente al valor analógico inicial es la que ya puede entender el computador. Imaginemos como ejemplo un convertidor A/D de 3 bits (8 palabras digitales de salida, de 000 a 111) cuyo margen de entrada es 5 V (5/8 = 0,625 V). Si a la entrada del convertidor llega un muestreo de 0,600 V, el valor asignado en la cuantificación será 0 V, el error de cuantificación cometido 0,6 V y la palabra digi-tal de salida 000.
En casos muy concretos donde la velocidad sea un factor determinante se puede implementar mediante hardware.
Un algoritmo es un procedimiento que puede llevar a una solución aproximada de un problema mediante un número finito de pasos que pueden ejecutarse de manera lógica.
Existen dos restricciones prácticas: 1) La consideración tiempo de muestreo menor implica mayor precisión llega un momento que se satura y deja de ser cierta, debido fundamentalmente a la propia precisión de cálculo del computador, y 2) Siempre es deseable llegar a un compromiso entre esfuerzo de cómputo o coste computacional y precisión.
Los métodos de Runge-Kutta son una familia de métodos iterativos para aproximar las soluciones de ecuaciones diferenciales ordinarias. Estas técnicas fueron desarrolladas alrededor de 1900 por los matemáticos alemanes Carl David Tolmé Runge y Martin Wilhelm Kutta.
En honor de su inventor, Leonhard Paul Euler. Matemático y físico que nació el 15 de abril de 1707 en Basilea (Suiza) y murió el 18 de septiembre de 1783 en San Petersburgo (Rusia). Es considerado el matemático principal del siglo XVIII y uno de los más grandes de todos los tiempos.
Para saber más ver por ejemplo http://es.wikipedia.org/wiki/Frecuencia_de_muestreo [50]
Para pares de transformadas, propiedades y, en general, para saber más sobre la transformada 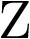 , véase por ejemplo http://es.wikipedia.org/wiki/Transformada_Z [51] La función de MATLAB ztrans permite calcular la transformada z de una secuencia.
, véase por ejemplo http://es.wikipedia.org/wiki/Transformada_Z [51] La función de MATLAB ztrans permite calcular la transformada z de una secuencia.
La función de MATLAB iztrans calcula la transformada z inversa.
Análisis del comportamiento dinámico de los sistemas
Este capítulo generaliza el concepto de modelo de estado, tanto desde el punto de vista continuo como discreto. Así se verá como recorrer el amplio espectro existente entre el caso más general, léase sistema no lineal variante con el tiempo, al más particular, sistema lineal e invariante con el tiempo. Esto es muy importante porque el lector debe tener siempre claro el rango de validez del modelo que está utilizando, de modo que debe evitar tanto cometer errores de modelado inasumibles, como sobreesfuerzos inútiles; ya que la mayoría de las veces los modelos admiten simplificaciones dentro de un rango de funcionamiento. A partir del modelo de estado de un sistema se pueden extraer múltiples enseñanzas de su comportamiento dinámico. Quizás la primera sea conocer la naturaleza de sus estados de equilibrio (o puntos singulares de su espacio de estado). Cuando el sistema es lineal, sólo puede tener un estado de equilibrio o un conjunto continuo de ellos (si la ecuación diferencial que lo modela no tiene término independiente); sin embargo, los sistemas no lineales pueden tener más de un estado de equilibrio. El análisis de los sistemas en su plano de fase (espacio de estado para sistemas de orden 2) caracteriza de forma cualitativa su comportamiento dinámico. Para los sistemas lineales éste depende sólo del carácter del estado de equilibrio, el cual queda definido por los autovalores de la matriz de estado; sin embargo, cuando los sistemas son no lineales, el carácter de los estados de equilibrio no es suficiente para entender su comportamiento global. Tanto es así que la riqueza dinámica de los mismos lleva a comportamientos sorprendentes, como los ciclos límite en los sistemas de orden 2 o incluso el caos en los de orden 3. Por último, si bien el conocimiento del comportamiento global de las trayectorias de un sistema no lineal puede ser una tarea muy compleja, el conocimiento local en torno a sus estados de equilibrio requiere menos esfuerzo, la mayoría de las veces basta con linealizar el sistema en torno a dichos estados. A partir de ahí, el estudio de los autovalores de la matriz de estado resultante (la matriz Jacobiana en este caso) permite realizar interpretaciones locales similares a las realizadas a nivel global para los sistemas lineales.
Si bien en el capítulo anterior nuestro estudio se ha centrado en los sistemas lineales, bien porque puedan ser considerados como tales o porque puedan ser linealizados en una zona concreta de funcionamiento, el mundo que nos rodea es esencialmente no lineal. En consecuencia, se ha de tener siempre muy presente esta circunstancia, de modo que el deseo lógico de simplificar los problemas (hacerlos lineales) no lleve a cometer errores inasumibles.
En base a la visión adquirida en el capítulo anterior, en esta sección se va a generalizar el con-cepto de modelo de estado. Así, un sistema completamente general (se entiende que puede ser no lineal y variante con el tiempo) puede ser representado por un modelo de estado consistente en un número finito de ecuaciones diferenciales de primer orden:
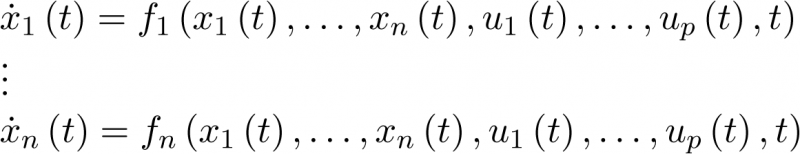 |
(3.1) |
Definiendo los vectores
![\[{\bf{\dot x}}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ \vdots \\ {{{\dot x}_n}\left( t \right)} \\ \end{array}} \right);\,\,\,\,{\bf{u}}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{u_1}\left( t \right)} \\ \vdots \\ {{u_p}\left( t \right)} \\ \end{array}} \right);\,\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-2a%283.2%29.png) ![\[\,{\bf{f}}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right),t} \right) = \left( {\begin{array}{*{20}{c}} {{f_1}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right),t} \right)} \\ \vdots \\ {{f_n}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right),t} \right)} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-2b%283.2%29.png) |
(3.2) |
La ecuación (3.1) puede ser escrita de la forma compacta
![\[\,{\bf{\dot x}}\left( t \right) = \,{\bf{f}}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right),t} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-3%283.3%29.png) |
(3.3) |
Del mismo modo, la ecuación de salida del sistema se escribirá como
![\[\,{\bf{y}}\left( t \right) = \,{\bf{h}}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right),t} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-4%283.4%29.png) |
(3.4) |
Las ecuaciones (3.3) y (3.4) representan el modelo de estado en tiempo continuo de un sistema completamente general.
Si las ecuaciones de estado y salida anteriores son lineales en el estado x y en la entrada u, el modelo puede ser representado como
![\[\begin{array}{*{20}{c}} {{\bf{\dot x}}\left( t \right) = \,{\bf{A}}\left( t \right){\bf{x}}\left( t \right) + {\bf{B}}\left( t \right){\bf{u}}\left( t \right)} \\ {{\bf{y}}\left( t \right) = \,{\bf{C}}\left( t \right){\bf{x}}\left( t \right) + {\bf{D}}\left( t \right){\bf{u}}\left( t \right)} \\ \end{array},\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-5%283.5%29.png) |
(3.5) (3.6) |
Donde las dimensiones de los vectores y las matrices ya fueron definidas en el capítulo anterior. Si el sistema además de lineal es invariante (LTI), las matrices tienen sus elementos constantes, con lo cual el modelo se escribirá en la forma ya conocida siguiente:
![\[\,\begin{array}{*{20}{c}} {{\bf{\dot x}}\left( t \right) = \,{\bf{Ax}}\left( t \right) + {\bf{Bu}}\left( t \right)} \\ {\,{\bf{y}}\left( t \right) = \,{\bf{Cx}}\left( t \right) + {\bf{Du}}\left( t \right)} \\ \end{array}.\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-6%283.7%29.png) |
(3.7) (3.8) |
El modelo de estado general (3.3) – (3.4) se escribirá para tiempo discreto en la forma
![\[\begin{array}{*{20}{c}} {{\bf{x}}\left( {k + 1} \right) = \,{{\bf{f}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right),{\bf{u}}\left( k \right),k} \right)} \\ {{\bf{y}}\left( k \right) = \,{{\bf{h}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right),{\bf{u}}\left( k \right),k} \right)} \\ \end{array}.\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-7%283.9%29.png) |
(3.9) (3.10) |
Del mismo modo que en el caso continuo, si las ecuaciones anteriores son lineales en el estado y en la entrada, el modelo puede ser representado como
![\[\,\begin{array}{*{20}{c}} {{\bf{x}}\left( {k + 1} \right) = \,{{\bf{A}}_{\bf{k}}}\left( k \right){\bf{x}}\left( k \right) + {{\bf{B}}_{\bf{k}}}\left( k \right){\bf{u}}\left( k \right)} \\ {\,{\bf{y}}\left( k \right) = \,{{\bf{C}}_{\bf{k}}}\left( k \right){\bf{x}}\left( k \right) + {{\bf{D}}_{\bf{k}}}\left( k \right){\bf{u}}\left( k \right)} \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-8%283.11%29.png) |
(3.11) |
Por último, para el caso LTI,
![\[\,\begin{array}{*{20}{c}} {{\bf{x}}\left( {k + 1} \right) = \,{{\bf{A}}_{\bf{k}}}{\bf{x}}\left( k \right) + {{\bf{B}}_{\bf{k}}}{\bf{u}}\left( k \right)} \\ {\,{\bf{y}}\left( k \right) = \,{{\bf{C}}_{\bf{k}}}{\bf{x}}\left( k \right) + {{\bf{D}}_{\bf{k}}}{\bf{u}}\left( k \right)} \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-9%283.12%29.png) |
(3.12) |
Casos especiales
Ecuación de estado no forzada. Se da cuando la entrada externa al sistema es idénticamente cero, en cuyo caso la ecuación de estado (3.3) se escribe como
![\[\,{\bf{\dot x}}\left( t \right) = \,{\bf{f}}\left( {{\bf{x}}\left( t \right),t} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-10%283.13%29.png) |
(3.13) |
Nótese que la ecuación no forzada (3.13) tendrá esa misma expresión tanto si 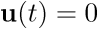 como si u(t) se obtiene a partir del vector de estado,
como si u(t) se obtiene a partir del vector de estado, 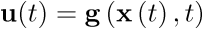 ; ya que sustituyendo
; ya que sustituyendo 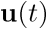 en (3.3), éste se elimina y vuelve a quedar la ecuación no forzada (3.13).
en (3.3), éste se elimina y vuelve a quedar la ecuación no forzada (3.13).
Sistema autónomo. Se da cuando el argumento de la función dada en (3.13) no depende del tiempo, en cuyo caso la ecuación de estado del sistema se escribe en la forma siguiente:
![\[\,{\bf{\dot x}}\left( t \right) = \,{\bf{f}}\left( {{\bf{x}}\left( t \right)} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-14%283.14%29.png) |
(3.14) |
Los sistemas autónomos son de importancia especial en automática y cumplen, entre otras propiedades, la de ser invariantes a cambios en el origen del tiempo. Esto quiere decir que si la variable t es cambiada por 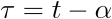 , la ecuación de estado permanece invariante.
, la ecuación de estado permanece invariante.
Los casos especiales (3.13) y (3.14) siguen siendo igualmente válidos para tiempo discreto, sin más que cambiar t por k, FALTAAAAAAAAAA(${\bf{\dot x}}\left( t \right)$) por 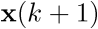 y f por fk.
y f por fk.
Ejemplo 3.1. Sistema mecánico no lineal. En el ejemplo 2.1 se resolvió el sistema muelle – masa – resorte para el caso en que todos sus elementos eran lineales. Supóngase ahora que el com-portamiento del muelle no es lineal, de modo que la fuerza necesaria para estirarlo aumenta con el desplazamiento del modo siguiente:
![\[\,{f_k}\left( t \right) = \,ky\left( t \right)\left( {1 + \alpha {y^2}\left( t \right)} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-17%283.15%29.png) |
(3.15) |
Donde 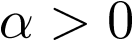 es una constante. Ahora, la ecuación diferencial (2.2) se escribirá como
es una constante. Ahora, la ecuación diferencial (2.2) se escribirá como
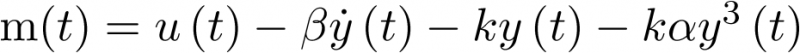 |
(3.16) |
Designando las variables de estado como 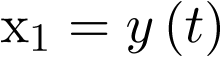 y
y 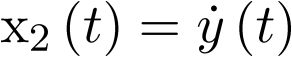 , se tiene en la ecuación anterior que
, se tiene en la ecuación anterior que
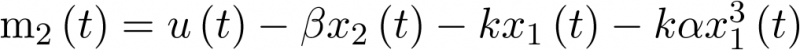 |
(3.17) |
A partir de aquí la ecuación vectorial de estado se obtiene de forma inmediata:
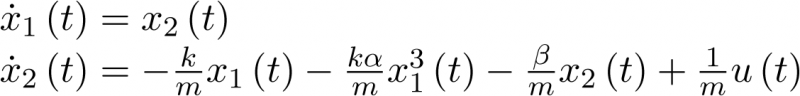 |
(3.18) |
Nótese que la ecuación anterior es de la forma 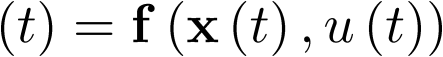 , donde f es una función no lineal en el estado
, donde f es una función no lineal en el estado ![\[{\bf{x}}\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-25.png) ; sin embargo, en este caso concreto, la ecuación de salida de este sistema,
; sin embargo, en este caso concreto, la ecuación de salida de este sistema,  , es lineal.
, es lineal.
En particular, si  , la ecuación (3.18) se transforma en el sistema autónomo no lineal
, la ecuación (3.18) se transforma en el sistema autónomo no lineal 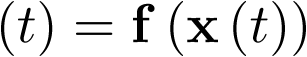 siguiente:
siguiente:
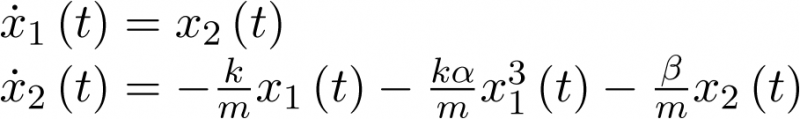 |
(3.19) |
Por supuesto, la no consideración1 [52] del término no lineal ![\[x_1^3\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-30.png) en (3.18) conduce al sistema lineal ya visto en (2.2):
en (3.18) conduce al sistema lineal ya visto en (2.2):
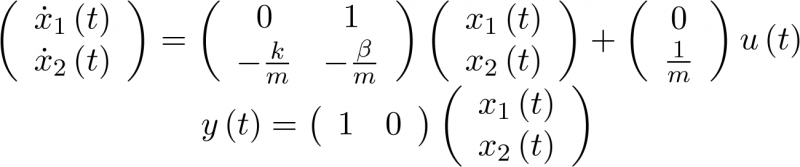 |
(3.20) |
La función de transferencia de este modelo de estado se obtuvo en el ejemplo (2.8).
Para tiempo discreto la ecuación (3.18) se escribe de la forma:
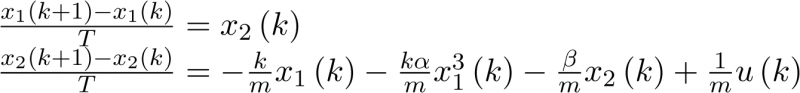 |
(3.21) |
Esto es,
![$\begin{array}{*{20}{c}} {{x_1}\left( {k + 1} \right) = {x_1}\left( k \right) + T{x_2}\left( k \right)} \hfill \\ {{x_2}\left( {k + 1} \right) = - \frac{{\,kT}}{m}\left[ {1 + \alpha x_1^2\left( k \right)} \right]{x_1}\left( k \right) + \left( {1 - \frac{{\beta T}}{m}} \right){x_2}\left( k \right) + \frac{T}{m}u\left( k \right)} \hfill \\ \end{array}$](/antonio.barragan/files/archivos_usuarios/78/form3.1-33%283.22%29.png) |
(3.22) |
Nótese que el modelo anterior es de la forma 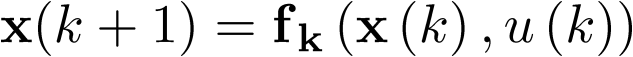 , donde fk es una función no lineal en el estado discreto
, donde fk es una función no lineal en el estado discreto 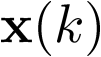 ; sin embargo, la ecuación de salida
; sin embargo, la ecuación de salida 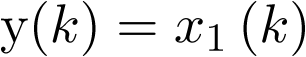 es lineal.
es lineal.
En particular, si  , la ecuación (3.22) se transforma en el sistema autónomo discreto no lineal
, la ecuación (3.22) se transforma en el sistema autónomo discreto no lineal 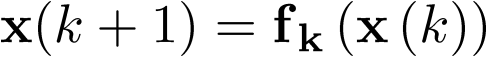 siguiente:
siguiente:
![$\begin{array}{*{20}{c}} {{x_1}\left( {k + 1} \right) = {x_1}\left( k \right) + T{x_2}\left( k \right)} \hfill \\ {{x_2}\left( {k + 1} \right) = - \frac{{kT\,}}{m}\left[ {1 + \alpha x_1^2\left( k \right)} \right]{x_1}\left( k \right) + \left( {1 - \frac{{\beta T}}{m}} \right){x_2}\left( k \right)} \hfill \\ \end{array}$](/antonio.barragan/files/archivos_usuarios/78/form3.1-39%283.23%29.png) |
(3.23) |
Nótese que el paso de (3.19) a (3.23) no es inmediato Por último, desestimando el término no lineal 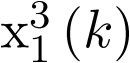 en (3.22), se llega al modelo de estado lineal
en (3.22), se llega al modelo de estado lineal
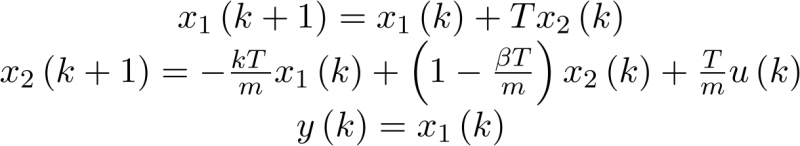 |
(3.24) |
Que en forma matricial se escribirá como:
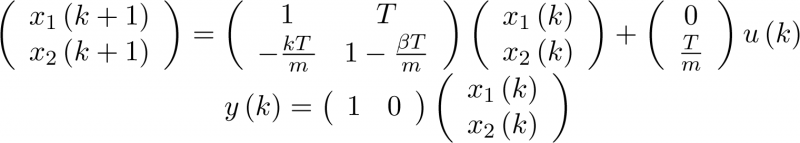 |
(3.25) |
El modelo anterior es claramente de la forma (3.12), con 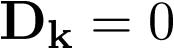 .
.
La función de transferencia G(z) de este modelo de estado discreto se obtiene a partir de las expresiones (2.146) y (2.147) del modo siguiente:
![\[\left( {z{\rm{I}} - {{\rm{A}}_{\rm{k}}}} \right) = \left( {\left( {\begin{array}{*{20}{c}} z & 0 \\ 0 & z \\ \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 1 & T \\ { - \frac{{kT}}{m}} & {1 - \frac{{\beta T}}{m}} \\ \end{array}} \right)} \right) = \left( {\begin{array}{*{20}{c}} {z - 1} & { - T} \\ {\frac{{kT}}{m}} & {z - 1 + \frac{{\beta T}}{m}} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-44%283.26%29.png) |
(3.26) |
Por consiguiente,
![\[\begin{array}{*{20}{c}} {{\bf{\Phi }}\left( z \right) = {{\left( {{\rm{zI}} - {{\rm{A}}_{\rm{k}}}} \right)}^{ - 1}} = \frac{1}{{\Delta \left( z \right)}}\left( {\begin{array}{*{20}{c}} {z - 1 + \frac{{\beta T}}{m}} & T \\ { - \frac{{kT}}{m}} & {z - 1} \\ \end{array}} \right);{\rm{ donde }}\Delta \left( z \right) = \left| {\begin{array}{*{20}{c}} {z - 1} & { - T} \\ {\frac{{kT}}{m}} & {z - 1 + \frac{{\beta T}}{m}} \\ \end{array}} \right|} \\ { = {z^2} + \left( {\frac{{\beta T}}{m} - 2} \right)z + \frac{T}{m}\left( {kT - \beta } \right) + 1} \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-45%283.27%29.png) |
(3.27) |
A partir de aquí, aplicando (2.146), se obtiene de forma inmediata la función de transferencia del modelo de estado discreto:
![\[\begin{array}{*{20}{c}} {G\left( z \right) = \frac{{Y\left( z \right)}}{{U\left( z \right)}} = {{\bf{C}}_{\bf{k}}}{\bf{\Phi }}\left( z \right){{\bf{B}}_{\bf{k}}} + {{\bf{D}}_{\bf{k}}} = \left( {\begin{array}{*{20}{c}} 1 & 0 \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\frac{{z - 1 + \frac{{\beta T}}{m}}}{{\Delta \left( z \right)}}} & {\frac{T}{{\Delta \left( z \right)}}} \\ {\frac{{ - \frac{{kT}}{m}}}{{\Delta \left( z \right)}}} & {\frac{{z - 1}}{{\Delta \left( z \right)}}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} 0 \\ {\frac{T}{m}} \\ \end{array}} \right) + 0 = \frac{{{{{T^2}} \mathord{\left/ {\vphantom {{{T^2}} m}} \right. \kern-\nulldelimiterspace} m}}}{{\Delta \left( z \right)}}} \\ { = \frac{{{{{T^2}} \mathord{\left/ {\vphantom {{{T^2}} m}} \right. \kern-\nulldelimiterspace} m}}}{{{z^2} + \left( {\frac{{\beta T}}{m} - 2} \right)z + \frac{T}{m}\left( {kT - \beta } \right) + 1}}} \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-46%283.28%29.png) |
(3.28) |
Nótese que a este mismo resultado se podría haber llegado de forma directa, esto es, aplicando la transformada ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-47%283.29%29.png) y el concepto de función de transferencia discreta sobre la ecuación en diferencias derivada de la ecuación diferencial (2.2), que caracteriza el comportamiento dinámico lineal del sistema:
y el concepto de función de transferencia discreta sobre la ecuación en diferencias derivada de la ecuación diferencial (2.2), que caracteriza el comportamiento dinámico lineal del sistema:
![\[m\ddot y\left( t \right) = u\left( t \right) - \beta \dot y\left( t \right) - ky\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-48%283.29%29.png) |
(3.29) |
Para convertir la ecuación anterior en una ecuación en diferencias hay que tener en cuenta la derivada segunda, la cual se discretiza de forma sencilla utilizando la aproximación de derivada en tiempo discreto dada por (2.92). Esto es,
![\[\begin{array}{*{20}{c}} {\ddot y\left( t \right) = \frac{d}{{dt}}\left( {\frac{{dy}}{{dt}}} \right) \approx \frac{d}{{dt}}\left[ {\frac{{y\left( {k + 1} \right) - y\left( k \right)}}{T}} \right] \approx \left[ {\frac{{\frac{{y\left( {k + 2} \right) - y\left( {k + 1} \right)}}{T} - \frac{{y\left( {k + 1} \right) - y\left( k \right)}}{T}}}{T}} \right]} \\ { = \frac{1}{{{T^2}}}\left[ {y\left( {k + 2} \right) - 2y\left( {k + 1} \right) + y\left( k \right)} \right]} \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-49%283.30%29.png) |
(3.30) |
Sustituyendo este valor en (3.29) se obtiene la ecuación en diferencias del sistema lineal:
![\[\frac{m}{{{T^2}}}\left[ {y\left( {k + 2} \right) - 2y\left( {k + 1} \right) + y\left( k \right)} \right] = u\left( k \right) - \beta \frac{{y\left( {k + 1} \right) - y\left( k \right)}}{T} - ky\left( k \right)\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-50%283.31%29.png) |
(3.31) |
Aplicando ahora a la ecuación anterior la transformada ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-47%283.29%29.png) con condiciones iniciales nulas,
con condiciones iniciales nulas,
![\[\frac{m}{{{T^2}}}\left[ {{z^2}Y\left( z \right) - 2zY\left( z \right) + Y\left( z \right)} \right] = U\left( z \right) - \beta \frac{{zY\left( z \right) - Y\left( z \right)}}{T} - kY\left( z \right)\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-51%283.32%29.png) |
(3.32) |
Esto es,
![\[\left[ {{z^2} + \left( {\frac{{\beta T}}{m} - 2} \right)z + \frac{T}{m}\left( {kT - \beta } \right) + 1} \right]Y\left( z \right) = \frac{{{T^2}}}{m}U\left( z \right)\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-52%283.33%29.png) |
(3.33) |
Luego de nuevo, como en (3.27),
![\[G\left( z \right) = \frac{{Y\left( z \right)}}{{U\left( z \right)}} = \frac{{{{{T^2}} \mathord{\left/ {\vphantom {{{T^2}} m}} \right. \kern-\nulldelimiterspace} m}}}{{{z^2} + \left( {\frac{{\beta T}}{m} - 2} \right)z + \frac{T}{m}\left( {kT - \beta } \right) + 1}}\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-53%283.34%29.png) |
(3.34) |
Dado el sistema autónomo 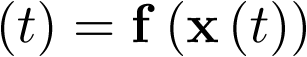 , se dice que el punto
, se dice que el punto 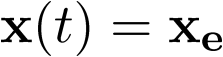 es un estado de equili-brio para dicho sistema, si cualquier trayectoria del mismo que comience en xe permanece en dicho punto por tiempo indefinido.
es un estado de equili-brio para dicho sistema, si cualquier trayectoria del mismo que comience en xe permanece en dicho punto por tiempo indefinido.
De acuerdo con la definición anterior y teniendo en cuenta que los estados de equilibrio xe de un sistema pertenecen a su espacio de estado, esto es, han de ser puntos reales, el cálculo de los mismos se realiza hallando las raíces reales de la ecuación:
![\[\,{\bf{\dot x}}\left( t \right) = \,{\bf{f}}\left( {{\bf{x}}\left( t \right)} \right) = {\bf{0}}\,\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-56%283.35%29.png) |
(3.35) |
La ecuación (3.35) puede no tener solución, que ésta sea única, varias soluciones o un continuo infinito de ellas. Obviamente, para los estados de equilibrio xe soluciones de (3.35) se cumple que
![\[\,{\bf{f}}\left( {{{\bf{x}}_{\bf{e}}}\left( t \right)} \right) = {\bf{0}}\,\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-57%283.36%29.png) |
(3.36) |
Del mismo modo, los estados de equilibrio xe del sistema autónomo en tiempo discreto 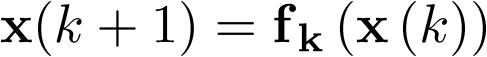 , serán aquellos que cumplan la condición
, serán aquellos que cumplan la condición
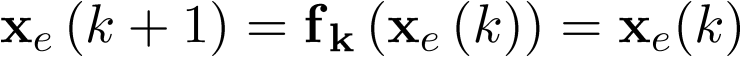 |
(3.37) |
Ejemplo 3.2. Sistema con un único estado de equilibrio. Sea el sistema lineal muelle – masa – amortiguador del ejemplo 2.1. El estado de equilibrio en su espacio de estado se obtendrá mediante la ecuación
![\[\,{\bf{\dot x}}\left( t \right) = {\bf{Ax}}\left( t \right) = {\bf{0}}\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-60%283.38%29.png) |
(3.38) |
la cual se escribirá para este sistema como
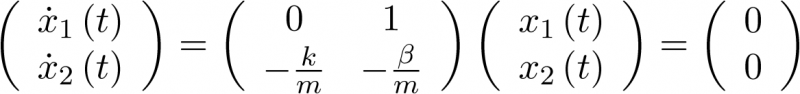 |
(3.39) |
La ecuación (3.38) tiene la solución única  si la matriz A es no singular2 [53]. Si A es singular, entonces tiene un continuo de soluciones (un continuo de estados de equilibrio), el espacio nulo de A. En el caso que nos atañe, ecuación (3.39), se ve claramente que el sistema tiene una única solución y por tanto un único estado de equilibrio en
si la matriz A es no singular2 [53]. Si A es singular, entonces tiene un continuo de soluciones (un continuo de estados de equilibrio), el espacio nulo de A. En el caso que nos atañe, ecuación (3.39), se ve claramente que el sistema tiene una única solución y por tanto un único estado de equilibrio en  .
.
Aunque este ejemplo pueda parecer trivial cabría preguntarse, ¿a partir de una condición inicial dada cualquiera, el sistema no forzado (sin entradas) va siempre al estado de equilibrio (0,0)? La pregunta se responde de forma inmediata si se conoce la evolución temporal del sistema a partir de la condición inicial, para lo cual bastaría con analizar la respuesta que ofrece la matriz de transición 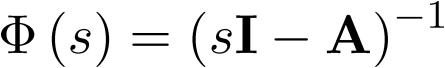 , ya que ésta representa el paso del sistema desde un estado inicial
, ya que ésta representa el paso del sistema desde un estado inicial 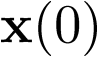 a otro considerado
a otro considerado 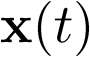 cuando la entrada es cero; esto es, caracteriza la respuesta no forzada o natural del sistema.
cuando la entrada es cero; esto es, caracteriza la respuesta no forzada o natural del sistema.
En el ejemplo 2.9 ya se trató este sistema en profundidad. Allí se vio cómo una matriz de transición con sus elementos formados por exponenciales negativas (2.85), origina una respuesta no forzada que lleva al sistema a su estado de equilibrio, en este caso situado en el (0,0), lo cual se comprueba gráficamente en las Figuras 2.9 y 2.10. ¿Qué provoca que las exponenciales sean negativas?, pues que el polinomio característico de la matriz de transición de un sistema continuo tenga sus raíces situadas en el eje real del semiplano izquierdo del plano complejo 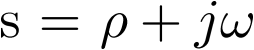 , esto es, que dichas raíces (polos del sistema) sean reales y negativas (para el caso de los sistemas discretos la respuesta no forzada lleva al sistema al estado de equilibrio si el polinomio característico tiene sus raíces dentro de un círculo con centro en el origen y radio unidad)3 [54].
, esto es, que dichas raíces (polos del sistema) sean reales y negativas (para el caso de los sistemas discretos la respuesta no forzada lleva al sistema al estado de equilibrio si el polinomio característico tiene sus raíces dentro de un círculo con centro en el origen y radio unidad)3 [54].
El hecho de que la respuesta natural del sistema tienda a cero hace que el sistema sea estable, esto es una entrada acotada siempre produce una salida acotada, ya que el régimen transitorio desaparece con el tiempo y al final el sistema responde a la entrada de forma limitada. Véase en la ecuación (2.89) como la respuesta del sistema a una entrada es la suma de la respuesta natural que desaparece con el tiempo (por eso el sistema no forzado va a su estado de equilibrio) más la respuesta forzada, que es la que queda al final (cuando desaparece el transitorio de la respuesta natural) como respuesta estacionaria o de régimen permanente del sistema a la excitación de entrada.
Comentario: El lector no debe perder de vista que el análisis de estabilidad tan simple realizado en este ejemplo sólo es posible porque el sistema es lineal.
 |
| Figura 3.1. (a) Circuito con diodo túnel. (b) Característica tensión – corriente de un diodo túnel típico. |
Ejemplo 3.3. Sistema con múltiples estados de equilibrio. Como ya se ha dicho, una característica que separa de forma notable los sistemas lineales de los no lineales son sus estados de equilibrio. Mientras que los primeros tienen sólo un estado de equilibrio o un continuo de ellos, los sistemas no lineales pueden tener múltiples estados de equilibrio, lo cual los dota de una riqueza dinámica extraordinaria. Para comenzar a ilustrar esto, que será ampliamente analizado a lo largo del capítulo, vamos a estudiar un circuito electrónico4 [55] (ver Figura 3.1 (a)) que permite explorar comportamientos dinámicos muy interesantes a pesar de ser sólo de segundo orden. La clave para ello está en uno de sus componentes, el diodo túnel o diodo Esaki5 [56] debido a su inventor. En la Figura 3.1 (b) se muestra una aproximación polinómica6 [57] de la curva característica vD - iD de un diodo túnel tipo. Esta aproximación está dada por la expresión:
![\[{i_D} = 17,76{v_D} - 103,79v_D^2 + 229,62v_D^3 - 226,31v_D^4 + 83,72v_D^5\]](/antonio.barragan/files/archivos_usuarios/78/form3.1-68.png) |
(3.40) |
Nótese en la característica del diodo túnel la gran no linealidad en su resistencia interna (ri), ya que si bien al principio la corriente crece con la tensión exhibiendo una pendiente (1/ri) casi constante, enseguida se llega a otra zona donde ocurre justo lo contrario (zona denominada de resistencia negativa). A continuación, después de un valle, el dispositivo vuelve a comportarse de forma normal.
Con objeto de calcular los estados de equilibrio de este circuito vamos a deducir en primer lugar su modelo de estado. Para ello se operará como en el ejemplo 2.4, siendo en este caso la entrada del sistema la fuente de tensión  . Sean pues las variables de estado
. Sean pues las variables de estado  y
y  . Considerando que el condensador y la bobina son elementos ideales, sus ecuaciones de definición estarán dadas por
. Considerando que el condensador y la bobina son elementos ideales, sus ecuaciones de definición estarán dadas por 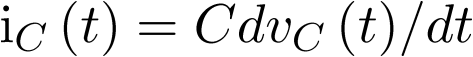 y
y 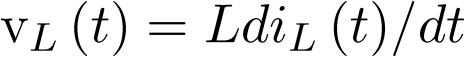 , con lo cual el modelo de estado puede ser planteado del modo siguiente:
, con lo cual el modelo de estado puede ser planteado del modo siguiente:
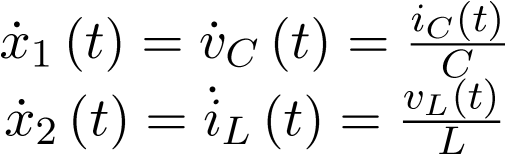 |
(3.41) |
Aplicando la ley de Kirchhoff de corriente en el nudo superior de la Figura 3.1 (a) se tiene que
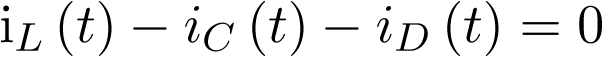 |
(3.42) |
Esto es,
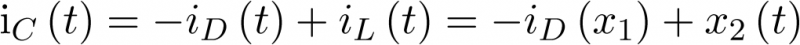 |
(3.43) |
Donde se ha enfatizado el hecho que iD es una función de vD y, por tanto, de x1. La expresión anterior permite completar la primera ecuación de estado. Respecto de la segunda, ésta se completa aplicando la ley de Kirchhoff de tensiones al lazo RLC. En él se cumple que
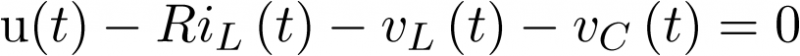 |
(3.44) |
Esto es,
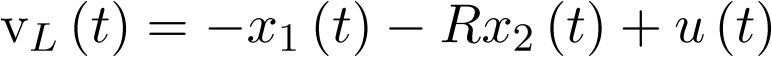 |
(3.45) |
Sustituyendo (3.43) y (3.45) en la ecuación de estado (3.41) se tiene el modelo siguiente:
![$\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right) = \frac{1}{C}\left[ { - {i_D}\left( {{x_1}} \right) + {x_2}\left( t \right)} \right]} \\ {{{\dot x}_2}\left( t \right) = \frac{1}{L}\left[ { - {x_1}\left( t \right) - R{x_2}\left( t \right) + u\left( t \right)} \right]} \\ \end{array}$](/antonio.barragan/files/archivos_usuarios/78/form3.1-78%283.46%29.png) |
(3.46) |
Los estados de equilibrio se obtienen igualando a cero las dos ecuaciones anteriores, lo cual permite obtener la expresión:
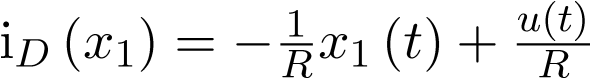 |
(3.47) |
Para una entrada constante la expresión anterior puede ser escrita como
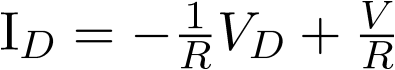 |
(3.48) |
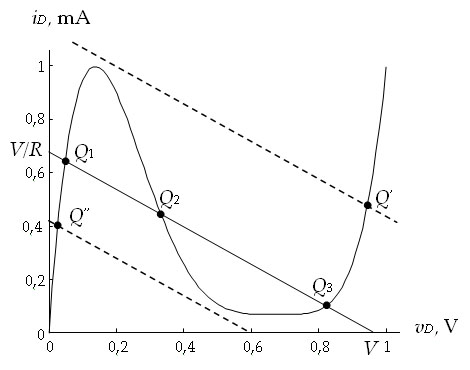 |
| Figura 3.2. Estados de equilibrio del circuito con diodo túnel. |
La cual, dibujada sobre la característica del diodo túnel, representa una recta de pendiente -1/R y puntos de corte con los ejes (V, V/R). Por tanto, dependiendo de los valores de V y R las soluciones del sistema de ecuaciones que proporciona los estados de equilibrio serán diferentes. Así, en la Figura 3.2 se muestran las distintas situaciones que pueden darse con 1 o 3 estados de equilibrio7. Nótese que manteniendo R constante (pendiente fija), la señal de control (la tensión u(t), V en la Figura 3.2) permite que el sistema tenga un único estado de equilibrio (Q’ o Q’’) o tres (Q1, Q2 y Q3). Más adelante en el capítulo veremos que en realidad el sistema sólo tiene dos estados de equilibrio estables, Q1 y Q3, con lo cual la señal de control podrá hacer bascular el funcionamiento de uno a otro permitiendo que el circuito se comporte de forma biestable.
Vamos a concretar ahora el cálculo de los estados de equilibrio del circuito con diodo túnel asumiendo que sus parámetros son u(t) = 1 V, R = 1,25 KΩ, C = 4 pF, L = 10 μH. Para estos valores y, teniendo en cuenta que las corrientes se miden en mA y las tensiones en voltios, el tiempo (ver ecuación (3.46)) vendrá dado en nanosegundos. Insertando estos valores en la ecuación de estado del circuito (3.47) se tiene que
El lector no debe confundir no considerar un término no lineal con linealizar un sistema no lineal, ya que no es lo mismo.
Dada una matriz cuadrada A, se dice que es no singular si su determinante no es cero (todos sus autovalores son distintos de cero). En caso contrario se dice que la matriz A es singular o degenerada. La consecuencia principal de que una matriz cuadrada tenga su determinante nulo es que no es invertible.
Esto se estudiará en el capítulo 4.
Tomado de L. O. Chua, C. A. Desoer, and E. S. Kuh. Linear and Nonlinear Circuits. McGraw-Hill, New York, 1987.
Es un tipo de diodo semiconductor que, entre otras características, es capaz de operar a muy alta frecuencia (en la región de las microondas, 300 MHz – 300 GHz) debido a que en su funcionamiento utiliza un efecto de la mecánica cuántica denominado efecto túnel. A grandes rasgos, este efecto permite que una partícula pueda salvar una barrera de potencial sin tener energía suficiente para rebasarla por encima (en el sentido clásico); para ello, al llegar a la barrera y a escala cuántica, la partícula exhibe un comportamiento ondulatorio (inmaterial) que le permite atravesar la barrera de potencial como si horadara un túnel para ello. El diodo túnel fue inventado en Agosto de 1957 por Leo Esaki, cuando trabajaba en la compañía Tokyo Tsushin Kogyo, conocida hoy en día como Sony. En 1973 recibió el premio Nobel en Física, junto con Brian Josephson, por descubrir el efecto túnel que rige el funcionamiento de estos diodos.
Tomada de H. K. Khalil,. Nonlinear Systems. Prentice-Hall, New Jersey, 2000.
Enlaces:
[1] http://uhu.es/antonio.barragan
[2] http://uhu.es/etsi
[3] http://uhu.es
[4] http://uhu.es/antonio.barragan/content/descargue-wikiapuntes-formato-electronico
[5] http://uhu.es/antonio.barragan/content/1
[6] http://uhu.es/antonio.barragan/content/2
[7] http://uhu.es/antonio.barragan/content/3
[8] http://uhu.es/antonio.barragan/content/4
[9] http://uhu.es/antonio.barragan/content/5
[10] http://uhu.es/antonio.barragan/content/6
[11] http://uhu.es/antonio.barragan/content/7
[12] http://uhu.es/antonio.barragan/content/8
[13] http://uhu.es/antonio.barragan/content/11
[14] http://uhu.es/antonio.barragan/content/12
[15] http://uhu.es/antonio.barragan/content/13
[16] http://uhu.es/antonio.barragan/content/14
[17] http://uhu.es/antonio.barragan/content/16
[18] http://uhu.es/antonio.barragan/content/17
[19] http://uhu.es/antonio.barragan/content/18
[20] http://uhu.es/antonio.barragan/content/19
[21] http://uhu.es/antonio.barragan/content/20
[22] http://uhu.es/antonio.barragan/content/21
[23] http://uhu.es/antonio.barragan/content/1-0
[24] http://uhu.es/antonio.barragan/content/2-0
[25] http://uhu.es/antonio.barragan/content/3-0
[26] http://uhu.es/antonio.barragan/content/4-0
[27] http://uhu.es/antonio.barragan/content/5-0
[28] http://uhu.es/antonio.barragan/content/6-0
[29] http://uhu.es/antonio.barragan/content/7-0
[30] http://uhu.es/antonio.barragan/content/8-0
[31] http://uhu.es/antonio.barragan/content/9-0
[32] http://uhu.es/antonio.barragan/content/10-0
[33] http://uhu.es/antonio.barragan/content/11-0
[34] http://uhu.es/antonio.barragan/content/12-0
[35] http://uhu.es/antonio.barragan/content/13-0
[36] http://uhu.es/antonio.barragan/content/14-0
[37] http://uhu.es/antonio.barragan/content/15-0
[38] http://uhu.es/antonio.barragan/content/17-0
[39] http://uhu.es/antonio.barragan/content/18-0
[40] http://uhu.es/antonio.barragan/content/20-0
[41] http://uhu.es/antonio.barragan/content/21-0
[42] http://uhu.es/antonio.barragan/content/22
[43] http://uhu.es/antonio.barragan/content/23
[44] http://uhu.es/antonio.barragan/content/24
[45] http://uhu.es/antonio.barragan/content/25
[46] http://uhu.es/antonio.barragan/content/26
[47] http://es.wikipedia.org/wiki/Serie_de_Taylor
[48] http://es.wikipedia.org/wiki/Transformada_de_Laplace
[49] http://www.scribd.com/doc/6075394/DescomposiciOn-Fracciones-Parciales
[50] http://es.wikipedia.org/wiki/Frecuencia_de_muestreo
[51] http://es.wikipedia.org/wiki/Transformada_Z
[52] http://uhu.es/antonio.barragan/content/1-1
[53] http://uhu.es/antonio.barragan/content/2-1
[54] http://uhu.es/antonio.barragan/content/3-1
[55] http://uhu.es/antonio.barragan/content/4-1
[56] http://uhu.es/antonio.barragan/content/5-1
[57] http://uhu.es/antonio.barragan/content/6-1