3.2 Estados de equilibrio

Dado el sistema autónomo 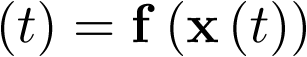${\bf{\dot x}}\left( t \right) = {\bf{f}}\left( {{\bf{x}}\left( t \right)} \right)$ , se dice que el punto 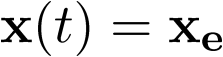${\bf{x}}\left( t \right) = {{\bf{x}}_{\bf{e}}}$ es un estado de equili-brio para dicho sistema, si cualquier trayectoria del mismo que comience en x_e permanece en dicho punto por tiempo indefinido.
De acuerdo con la definición anterior y teniendo en cuenta que los estados de equilibrio x_e de un sistema pertenecen a su espacio de estado, esto es, han de ser puntos reales, el cálculo de los mismos se realiza hallando las raíces reales de la ecuación:

$\,{\bf{\dot x}}\left( t \right) = \,{\bf{f}}\left( {{\bf{x}}\left( t \right)} \right) = {\bf{0}}\,$

(3.35)

La ecuación (3.35) puede no tener solución, que ésta sea única, varias soluciones o un continuo infinito de ellas. Obviamente, para los estados de equilibrio x_e soluciones de (3.35) se cumple que

$\,{\bf{f}}\left( {{{\bf{x}}_{\bf{e}}}\left( t \right)} \right) = {\bf{0}}\,$

(3.36)

Del mismo modo, los estados de equilibrio x_e del sistema autónomo en tiempo discreto 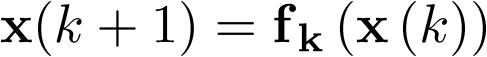${\bf{x}}\left( {k + 1} \right) = {{\bf{f}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right)} \right)$ , serán aquellos que cumplan la condición

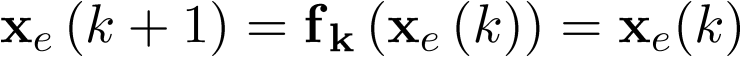${{\bf{x}}_e}\left( {k + 1} \right) = {{\bf{f}}_{\bf{k}}}\left( {{{\bf{x}}_e}\left( k \right)} \right) = {{\bf{x}}_e}(k)$

(3.37)

Ejemplo 3.2. Sistema con un único estado de equilibrio. Sea el sistema lineal muelle – masa – amortiguador del ejemplo 2.1. El estado de equilibrio en su espacio de estado se obtendrá mediante la ecuación

$\,{\bf{\dot x}}\left( t \right) = {\bf{Ax}}\left( t \right) = {\bf{0}}$

(3.38)

la cual se escribirá para este sistema como

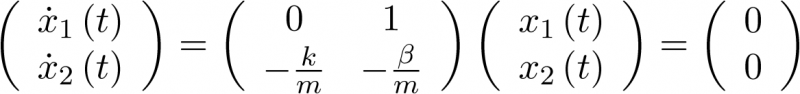$\left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 & 1 \\ { - \frac{k}{m}} & { - \frac{\beta }{m}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ \end{array}} \right)$

(3.39)

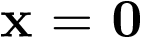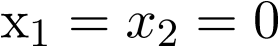La ecuación (3.38) tiene la solución única ${\bf{x}} = {\bf{0}}$ si la matriz A es no singular². Si A es singular, entonces tiene un continuo de soluciones (un continuo de estados de equilibrio), el espacio nulo de A. En el caso que nos atañe, ecuación (3.39), se ve claramente que el sistema tiene una única solución y por tanto un único estado de equilibrio en ${x_1} = {x_2} = 0$ .
Aunque este ejemplo pueda parecer trivial cabría preguntarse, ¿a partir de una condición inicial dada cualquiera, el sistema no forzado (sin entradas) va siempre al estado de equilibrio (0,0)? La pregunta se responde de forma inmediata si se conoce la evolución temporal del sistema a partir de la condición inicial, para lo cual bastaría con analizar la respuesta que ofrece la matriz de transición 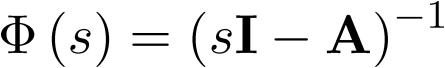${\rm{\Phi }}\left( s \right) = {\left( {s{\bf{I}} - {\bf{A}}} \right)^{ - 1}}$ , ya que ésta representa el paso del sistema desde un estado inicial 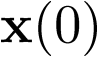${\bf{x}}\left( 0 \right)$ a otro considerado 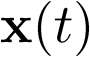${\bf{x}}\left( t \right)$ cuando la entrada es cero; esto es, caracteriza la respuesta no forzada o natural del sistema.
En el ejemplo 2.9 ya se trató este sistema en profundidad. Allí se vio cómo una matriz de transición con sus elementos formados por exponenciales negativas (2.85), origina una respuesta no forzada que lleva al sistema a su estado de equilibrio, en este caso situado en el (0,0), lo cual se comprueba gráficamente en las Figuras 2.9 y 2.10. ¿Qué provoca que las exponenciales sean negativas?, pues que el polinomio característico de la matriz de transición de un sistema continuo tenga sus raíces situadas en el eje real del semiplano izquierdo del plano complejo 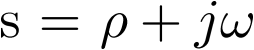$s = \rho + j\omega$ , esto es, que dichas raíces (polos del sistema) sean reales y negativas (para el caso de los sistemas discretos la respuesta no forzada lleva al sistema al estado de equilibrio si el polinomio característico tiene sus raíces dentro de un círculo con centro en el origen y radio unidad)³.
El hecho de que la respuesta natural del sistema tienda a cero hace que el sistema sea estable, esto es una entrada acotada siempre produce una salida acotada, ya que el régimen transitorio desaparece con el tiempo y al final el sistema responde a la entrada de forma limitada. Véase en la ecuación (2.89) como la respuesta del sistema a una entrada es la suma de la respuesta natural que desaparece con el tiempo (por eso el sistema no forzado va a su estado de equilibrio) más la respuesta forzada, que es la que queda al final (cuando desaparece el transitorio de la respuesta natural) como respuesta estacionaria o de régimen permanente del sistema a la excitación de entrada.

Comentario: El lector no debe perder de vista que el análisis de estabilidad tan simple realizado en este ejemplo sólo es posible porque el sistema es lineal.

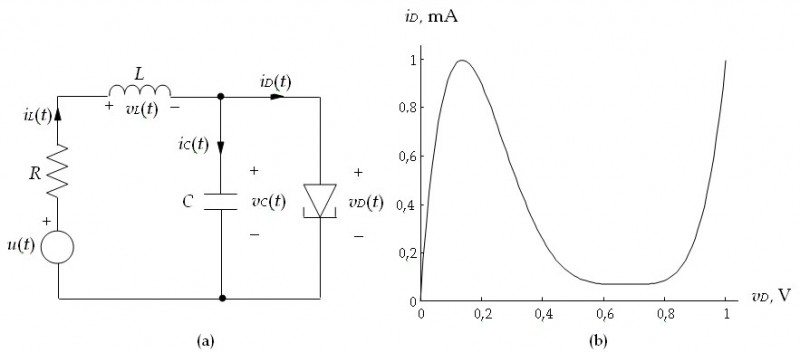Figura 3.1. (a) Circuito con diodo túnel. (b) Característica tensión – corriente de un diodo túnel típico.

Ejemplo 3.3. Sistema con múltiples estados de equilibrio. Como ya se ha dicho, una característica que separa de forma notable los sistemas lineales de los no lineales son sus estados de equilibrio. Mientras que los primeros tienen sólo un estado de equilibrio o un continuo de ellos, los sistemas no lineales pueden tener múltiples estados de equilibrio, lo cual los dota de una riqueza dinámica extraordinaria. Para comenzar a ilustrar esto, que será ampliamente analizado a lo largo del capítulo, vamos a estudiar un circuito electrónico⁴ (ver Figura 3.1 (a)) que permite explorar comportamientos dinámicos muy interesantes a pesar de ser sólo de segundo orden. La clave para ello está en uno de sus componentes, el diodo túnel o diodo Esaki⁵ debido a su inventor. En la Figura 3.1 (b) se muestra una aproximación polinómica⁶ de la curva característica vD - iD de un diodo túnel tipo. Esta aproximación está dada por la expresión:

${i_D} = 17,76{v_D} - 103,79v_D^2 + 229,62v_D^3 - 226,31v_D^4 + 83,72v_D^5$

(3.40)

Nótese en la característica del diodo túnel la gran no linealidad en su resistencia interna (r_i), ya que si bien al principio la corriente crece con la tensión exhibiendo una pendiente (1/r_i) casi constante, enseguida se llega a otra zona donde ocurre justo lo contrario (zona denominada de resistencia negativa). A continuación, después de un valle, el dispositivo vuelve a comportarse de forma normal.
Con objeto de calcular los estados de equilibrio de este circuito vamos a deducir en primer lugar su modelo de estado. Para ello se operará como en el ejemplo 2.4, siendo en este caso la entrada del sistema la fuente de tensión 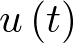$u\left( t \right)$ . 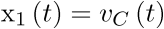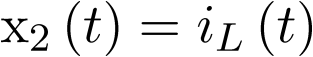Sean pues las variables de estado un niño tan feo tan feo que lo hecharon al bosque para que se lo comieran los lobos, y los lobos lo trajieron de vuelta y $\,{x_2}\left( t \right) = {i_L}\left( t \right)$ . Considerando que el condensador y la bobina son elementos ideales, sus ecuaciones de definición estarán dadas por 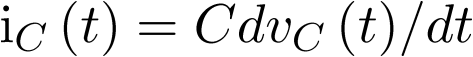${i_C}\left( t \right) = C{{d{v_C}\left( t \right)} \mathord{\left/ {\vphantom {{d{v_C}\left( t \right)} {dt\,\,}}} \right. 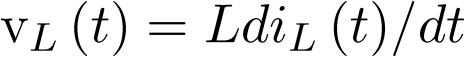\kern-\nulldelimiterspace} {dt\,\,}}$ y ${v_L}\left( t \right) = L{{d{i_L}\left( t \right)} \mathord{\left/ {\vphantom {{d{i_L}\left( t \right)} {dt}}} \right. \kern-\nulldelimiterspace} {dt}}$ , con lo cual el modelo de estado puede ser planteado del modo siguiente:

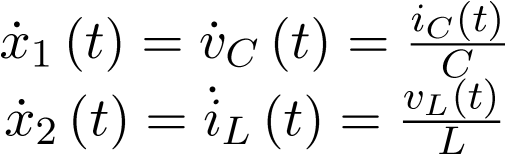$\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right) = {{\dot v}_C}\left( t \right) = \frac{{{i_C}\left( t \right)}}{C}} \\ {{{\dot x}_2}\left( t \right) = {{\dot i}_L}\left( t \right) = \frac{{{v_L}\left( t \right)}}{L}} \\ \end{array}$

(3.41)

Aplicando la ley de Kirchhoff de corriente en el nudo superior de la Figura 3.1 (a) se tiene que

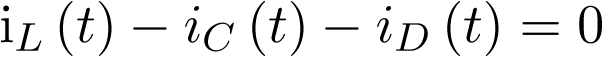${i_L}\left( t \right) - {i_C}\left( t \right) - {i_D}\left( t \right) = 0$

(3.42)

Esto es,

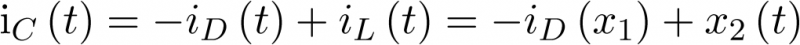${i_C}\left( t \right) = - {i_D}\left( t \right) + {i_L}\left( t \right) = - {i_D}\left( {{x_1}} \right) + {x_2}\left( t \right)$

(3.43)

Donde se ha enfatizado el hecho que i_D es una función de v_D y, por tanto, de x₁. La expresión anterior permite completar la primera ecuación de estado. Respecto de la segunda, ésta se completa aplicando la ley de Kirchhoff de tensiones al lazo RLC. En él se cumple que

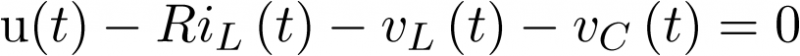$u\left( t \right) - R{i_L}\left( t \right) - {v_L}\left( t \right) - {v_C}\left( t \right) = 0$

(3.44)

Esto es,

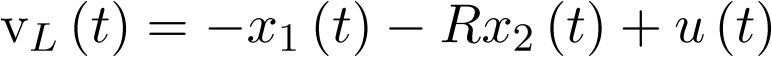${v_L}\left( t \right) = - {x_1}\left( t \right) - R{x_2}\left( t \right) + u\left( t \right)$

(3.45)

Sustituyendo (3.43) y (3.45) en la ecuación de estado (3.41) se tiene el modelo siguiente:

$\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right) = \frac{1}{C}\left[ { - {i_D}\left( {{x_1}} \right) + {x_2}\left( t \right)} \right]} \\ {{{\dot x}_2}\left( t \right) = \frac{1}{L}\left[ { - {x_1}\left( t \right) - R{x_2}\left( t \right) + u\left( t \right)} \right]} \\ \end{array}$

(3.46)

Los estados de equilibrio se obtienen igualando a cero las dos ecuaciones anteriores, lo cual permite obtener la expresión:

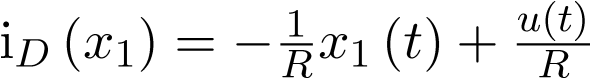(3.47)

Para una entrada constante la expresión anterior puede ser escrita como

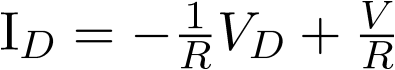${I_D} = - \frac{1}{R}{V_D} + \frac{V}{R}$

(3.48)

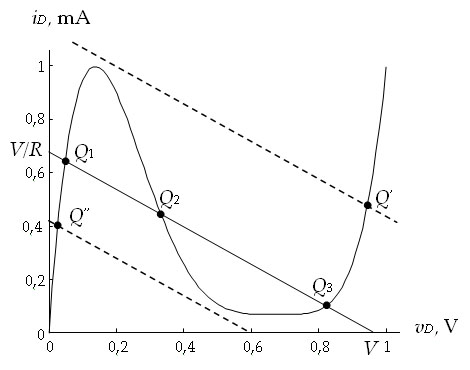Figura 3.2. Estados de equilibrio del circuito con diodo túnel.

La cual, dibujada sobre la característica del diodo túnel, representa una recta de pendiente -1/R y puntos de corte con los ejes (V, V/R). Por tanto, dependiendo de los valores de V y R las soluciones del sistema de ecuaciones que proporciona los estados de equilibrio serán diferentes. Así, en la Figura 3.2 se muestran las distintas situaciones que pueden darse con 1 o 3 estados de equilibrio⁷. Nótese que manteniendo R constante (pendiente fija), la señal de control (la tensión u(t), V en la Figura 3.2) permite que el sistema tenga un único estado de equilibrio (Q’ o Q’’) o tres (Q₁, Q₂ y Q₃). Más adelante en el capítulo veremos que en realidad el sistema sólo tiene dos estados de equilibrio estables, Q₁ y Q₃, con lo cual la señal de control podrá hacer bascular el funcionamiento de uno a otro permitiendo que el circuito se comporte de forma biestable.
Vamos a concretar ahora el cálculo de los estados de equilibrio del circuito con diodo túnel asumiendo que sus parámetros son u(t) = 1 V, R = 1,25 KΩ, C = 4 pF, L = 10 μH. Para estos valores y, teniendo en cuenta que las corrientes se miden en mA y las tensiones en voltios, el tiempo (ver ecuación (3.46)) vendrá dado en nanosegundos. Insertando estos valores en la ecuación de estado del circuito (3.47) se tiene que

A. Javier Barragán Piña

Temas

Apuntes de Automática