A. Javier Barragán Piña

Versión para imprimir

Vamos a estudiar la estabilidad del siguiente sistema teniendo en cuenta que la función de transferencia de G(z) es

$G(z)=\dfrac{0.3679z+0.2642}{(z-0.3679) (z-1)}$

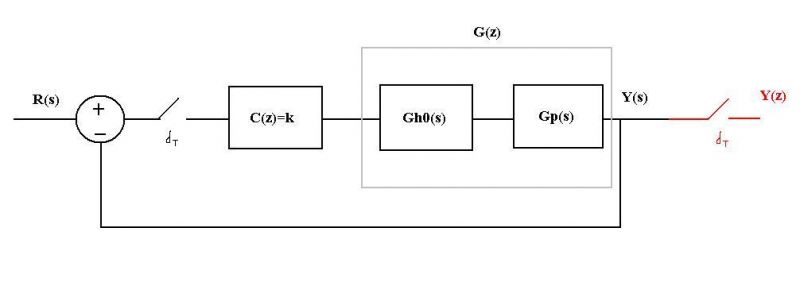
Vamos a obtener la función de transferencia del sistema en lazo cerrado.

$\dfrac{Y(z)}{R(z)}$

$E(s)=R(s)-Y(s)$  que de forma discreta es $E(z)=R(z)-Y(z)$

$U(z)=K E(z)$

$Y(z)=U(z)G(z)$

De las dos primeras ecuaciones obtenemos
$U(z)=K(R(z)-Y(z))=KR(z)-KY(z)$

Utilizando U(z) en la ecuación de Y(z) obtenemos

$Y(z)=U(z)G(z)=KR(z)G(z)-KY(z)G(z)$

$Y(z)(1+KG(z))=KR(z)G(z)$

Teniendo finalmente la función de transferencia pulso del sistema

$\dfrac{Y(z)}{R(z)}=\dfrac{KG(z)}{1+KG(z)}=$

La ecuación característica de un sistema es el denominador de la función de transferencia en lazo cerrado. Por lo tanto en nuestro ejemplo la ecuación característica es:

$E.C. \equiv 1+KG(z)=0$

Sustituyendo G(z) por el valor que nos indica el problema tenemos que:

$E.C.\equiv(1+K)\dfrac{0.3679z+0.2642}{(z-0.3679) (z-1)}=0$

Para aplicar el test de Jury tenemos que tener la ecuación característica en forma de polinomio, por lo que vamos a quitar el denominador de la fracción.

$(z-0.3679) (z-1)+K(0.3679z+0.2642)=0$

$z^2-1.3679z+0.3679+0.3679Kz+0.2642K=0$

$z^2+z(0.3679K-1.3679)+0.2642K+0.3679=0$

Una vez colocada en forma de polinomio vamos a aplicar el test de Jury. La matriz del test tendrá un número de filas 2n-3, siendo n el grado de la ecuación característica. En este caso 2n-3=2*2-3=1.

Condiciones del test de Jury

Ahora vamos a comprobar las condiciones del test para comprobar la estabilidad según los valores de K y de la E.C.

1) D(1)>0  Tenemos que comprobar que el valor de la E.C. evaluado en z=1 es mayor que 0.

$1+1(0.3679K-1.3679)+0.2642K+0.3679>0$

$(0.3679+0.2642)K>0$

Para que se cumpla esta inecuación, forzosamente K tiene que ser mayor que 0

2) $(-1)^n D(-1) >0$  Tenemos que comprobar que -1 elevado al grado de la ecuación multiplicado por la ecuación evaluada en z=-1 es mayor que 0. Como n=2, -1 elevado a 2 es 1, por lo que solo vamos a evaluar E.C. en z=-1.

$-1+(-1)(0.3679K-1.3679)+0.2642K+0.3679>0$

$1-0.3679K+1.3679+0.2642K+0.3679>0$

$2.7358-0.1037K>0$

$-K>\dfrac{-2.7358}{0.1037};K<26.382$

3) | a0 | < an  Esta condición la comprobamos utilizando la tabla del test de Jury. Como solo esta formada por una fila, tenemos que evaluar  únicamente una condición.

$0.2642K+0.3679<1$

$K<\dfrac{1-0.2642}{0.3679};K<2.3925$

Finalmente acotamos el valor de K para que cumpla las 3 inecuaciones obtenidas.

$1) K>0$

$2) K<26.382$

$3) K<2.3925$

Las que nos van a condicionar el valor de K son las inecuaciones 1 y 3, que nos van a limitar el valor de K para que sea estable. Por lo tanto K queda acotada de la siguiente forma:

$0< K<2.39$

nota: redondeamos en este caso a la baja para asegurarnos un margen a la hora de asignar un valor concreto a K.

De esta forma el sistema obtenido será estable.