Principal › Apuntes de Automática › CAPÍTULO 3 › 3.1 Modelo de estado de un sistema general. Casos especiales

Revisión de 3.1 Modelo de estado de un sistema general. Casos especiales de 26 July, 2011 - 19:33

20 July, 2011 - 14:48 — joaquinm13
Versión para imprimirVersión para imprimir

Si bien en el capítulo anterior nuestro estudio se ha centrado en los sistemas lineales, bien porque puedan ser considerados como tales o porque puedan ser linealizados en una zona concreta de funcionamiento,  el mundo que nos rodea es esencialmente no lineal. En consecuencia, se ha de tener siempre muy presente esta circunstancia, de modo que el deseo lógico de simplificar los problemas (hacerlos lineales) no lleve a cometer errores inasumibles.
En base a la visión adquirida en el capítulo anterior, en esta sección se va a generalizar el con-cepto de modelo de estado. Así, un sistema completamente general (se entiende que puede ser no lineal y variante con el tiempo) puede ser representado por un modelo de estado consistente en un número finito de ecuaciones diferenciales de primer orden:

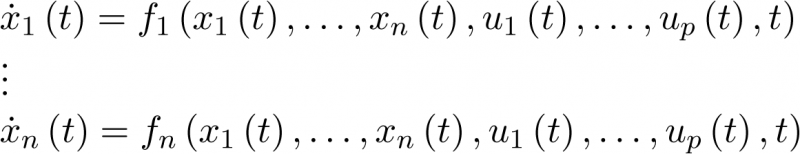(3.1) (3.1)

Definiendo los vectores

\[{\bf{\dot x}}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ \vdots \\ {{{\dot x}_n}\left( t \right)} \\ \end{array}} \right);\,\,\,\,{\bf{u}}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{u_1}\left( t \right)} \\ \vdots \\ {{u_p}\left( t \right)} \\ \end{array}} \right);\,\]\[\,{\bf{f}}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right),t} \right) = \left( {\begin{array}{*{20}{c}} {{f_1}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right),t} \right)} \\ \vdots \\ {{f_n}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right),t} \right)} \\ \end{array}} \right)\] (3.2)

La ecuación (3.1) puede ser escrita de la forma compacta

\[\,{\bf{\dot x}}\left( t \right) = \,{\bf{f}}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right),t} \right)\] (3.3)

Del mismo modo, la ecuación de salida del sistema se escribirá como

\[\,{\bf{y}}\left( t \right) = \,{\bf{h}}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right),t} \right)\] (3.4)

Las ecuaciones (3.3) y (3.4) representan el modelo de estado en tiempo continuo de un sistema completamente general.
Si las ecuaciones de estado y salida anteriores son lineales en el estado x y en la entrada u, el modelo puede ser representado como

\[\begin{array}{*{20}{c}} {{\bf{\dot x}}\left( t \right) = \,{\bf{A}}\left( t \right){\bf{x}}\left( t \right) + {\bf{B}}\left( t \right){\bf{u}}\left( t \right)} \\ {{\bf{y}}\left( t \right) = \,{\bf{C}}\left( t \right){\bf{x}}\left( t \right) + {\bf{D}}\left( t \right){\bf{u}}\left( t \right)} \\ \end{array},\] (3.5)
(3.6)

Donde las dimensiones de los vectores y las matrices ya fueron definidas en el capítulo anterior. Si el sistema además de lineal es invariante (LTI), las matrices tienen sus elementos constantes, con lo cual el modelo se escribirá en la forma ya conocida siguiente:

\[\,\begin{array}{*{20}{c}} {{\bf{\dot x}}\left( t \right) = \,{\bf{Ax}}\left( t \right) + {\bf{Bu}}\left( t \right)} \\ {\,{\bf{y}}\left( t \right) = \,{\bf{Cx}}\left( t \right) + {\bf{Du}}\left( t \right)} \\ \end{array}.\] (3.7)
(3.8)

El modelo de estado general (3.3) – (3.4) se escribirá para tiempo discreto en la forma

\[\begin{array}{*{20}{c}} {{\bf{x}}\left( {k + 1} \right) = \,{{\bf{f}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right),{\bf{u}}\left( k \right),k} \right)} \\ {{\bf{y}}\left( k \right) = \,{{\bf{h}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right),{\bf{u}}\left( k \right),k} \right)} \\ \end{array}.\] (3.9)
(3.10)

Del mismo modo que en el caso continuo, si las ecuaciones anteriores son lineales en el estado y en la entrada, el modelo puede ser representado como

\[\,\begin{array}{*{20}{c}} {{\bf{x}}\left( {k + 1} \right) = \,{{\bf{A}}_{\bf{k}}}\left( k \right){\bf{x}}\left( k \right) + {{\bf{B}}_{\bf{k}}}\left( k \right){\bf{u}}\left( k \right)} \\ {\,{\bf{y}}\left( k \right) = \,{{\bf{C}}_{\bf{k}}}\left( k \right){\bf{x}}\left( k \right) + {{\bf{D}}_{\bf{k}}}\left( k \right){\bf{u}}\left( k \right)} \\ \end{array}\] (3.11)

Por último, para el caso LTI,

\[\,\begin{array}{*{20}{c}} {{\bf{x}}\left( {k + 1} \right) = \,{{\bf{A}}_{\bf{k}}}{\bf{x}}\left( k \right) + {{\bf{B}}_{\bf{k}}}{\bf{u}}\left( k \right)} \\ {\,{\bf{y}}\left( k \right) = \,{{\bf{C}}_{\bf{k}}}{\bf{x}}\left( k \right) + {{\bf{D}}_{\bf{k}}}{\bf{u}}\left( k \right)} \\ \end{array}\] (3.12)

Casos especiales

Ecuación de estado no forzada. Se da cuando la entrada externa al sistema es idénticamente cero, en cuyo caso la ecuación de estado (3.3) se escribe como

\[\,{\bf{\dot x}}\left( t \right) = \,{\bf{f}}\left( {{\bf{x}}\left( t \right),t} \right)\] (3.13)

Nótese que la ecuación no forzada (3.13) tendrá esa misma expresión tanto si 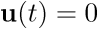${\bf{u}}\left( t \right) = 0$ como si u(t) se obtiene a partir del vector de estado, 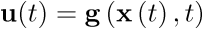${\bf{u}}\left( t \right) = {\bf{g}}\left( {{\bf{x}}\left( t \right),t} \right)$; ya que sustituyendo 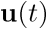${\bf{u}}\left( t \right)$ en (3.3), éste se elimina y vuelve a quedar la ecuación no forzada (3.13).

Sistema autónomo. Se da cuando el argumento de la función dada en (3.13) no depende del tiempo, en cuyo caso la ecuación de estado del sistema se escribe en la forma siguiente:

\[\,{\bf{\dot x}}\left( t \right) = \,{\bf{f}}\left( {{\bf{x}}\left( t \right)} \right)\] (3.14)

Los sistemas autónomos son de importancia especial en automática y cumplen, entre otras propiedades, la de ser invariantes a cambios en el origen del tiempo. Esto quiere decir que si la variable t es cambiada por 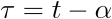$\tau = t - \alpha $, la ecuación de estado permanece invariante.
Los casos especiales (3.13) y (3.14) siguen siendo igualmente válidos para tiempo discreto, sin más que cambiar t por k, FALTAAAAAAAAAA(${\bf{\dot x}}\left( t \right)$) por 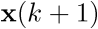${\bf{x}}\left( {k + 1} \right)$ y f por fk.

Ejemplo 3.1. Sistema mecánico no lineal. En el ejemplo 2.1 se resolvió el sistema muelle – masa – resorte  para el caso en que todos sus elementos eran lineales.  Supóngase ahora que el com-portamiento del muelle no es lineal, de modo que la fuerza necesaria para estirarlo aumenta con el desplazamiento del modo siguiente:

\[\,{f_k}\left( t \right) = \,ky\left( t \right)\left( {1 + \alpha {y^2}\left( t \right)} \right)\] (3.15)

Donde 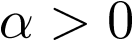$\alpha > 0$ es una constante. Ahora, la ecuación diferencial (2.2) se escribirá como

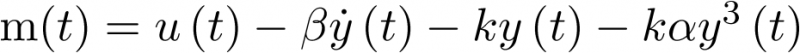$m\ddot y\left( t \right) = u\left( t \right) - \beta \dot y\left( t \right) - ky\left( t \right) - k\alpha {y^3}\left( t \right)$ (3.16)

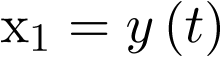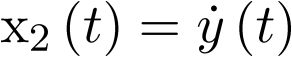Designando las variables de estado como ${x_1} = y\left( t \right)$ y ${x_2}\left( t \right) = \dot y\left( t \right)$, se tiene en la ecuación anterior que

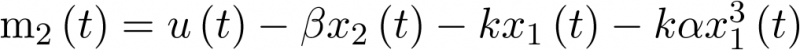$m{\dot x_2}\left( t \right) = u\left( t \right) - \beta {x_2}\left( t \right) - k{x_1}\left( t \right) - k\alpha x_1^3\left( t \right)$ (3.17)

A partir de aquí la ecuación vectorial de estado se obtiene de forma inmediata:

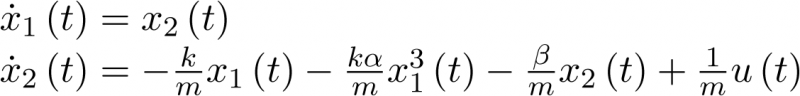$\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right) = {x_2}\left( t \right)} \hfill \\ {{{\dot x}_2}\left( t \right) = - \frac{k}{m}{x_1}\left( t \right) - \frac{{k\alpha }}{m}x_1^3\left( t \right) - \frac{\beta }{m}{x_2}\left( t \right) + \frac{1}{m}u\left( t \right)} \hfill \\ \end{array}$ (3.18)

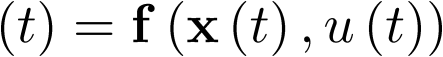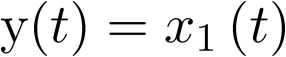Nótese que la ecuación anterior es de la forma ${\bf{\dot x}}\left( t \right) = {\bf{f}}\left( {{\bf{x}}\left( t \right),u\left( t \right)} \right)$, donde f es una función no lineal en el estado \[{\bf{x}}\left( t \right)\]; sin embargo, en este caso concreto, la ecuación de salida de este sistema, $y\left( t \right) = {x_1}\left( t \right)$, es lineal.
En particular, si 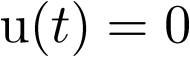$u\left( t \right) = 0$, la ecuación (3.18) se transforma en el sistema autónomo no lineal 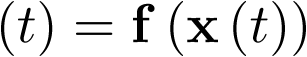${\bf{\dot x}}\left( t \right) = {\bf{f}}\left( {{\bf{x}}\left( t \right)} \right)$ siguiente:

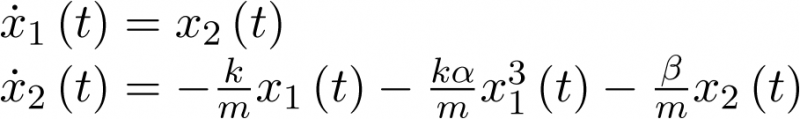$\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right) = {x_2}\left( t \right)} \hfill \\ {{{\dot x}_2}\left( t \right) = - \frac{k}{m}{x_1}\left( t \right) - \frac{{k\alpha }}{m}x_1^3\left( t \right) - \frac{\beta }{m}{x_2}\left( t \right)} \hfill \\ \end{array}$ (3.19)

Por supuesto, la no consideración1 del término no lineal \[x_1^3\left( t \right)\] en (3.18) conduce al sistema lineal ya visto en (2.2):

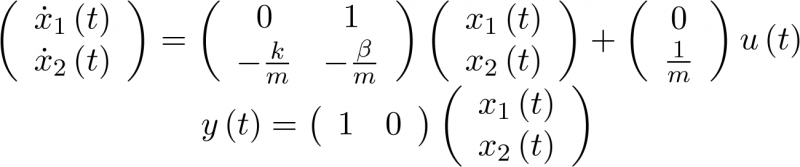$\begin{array}{c} \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 & 1 \\ { - \frac{k}{m}} & { - \frac{\beta }{m}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ {\frac{1}{m}} \\ \end{array}} \right)u\left( t \right) \\ y\left( t \right) = \left( {\begin{array}{*{20}{c}} 1 & 0 \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) \\ \end{array}$ (3.20)

La función de transferencia de este modelo de estado se obtuvo en el ejemplo (2.8).
Para tiempo discreto la ecuación (3.18) se escribe de la forma:

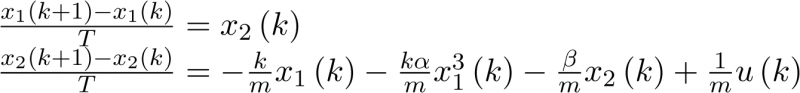$\begin{array}{*{20}{c}} {\frac{{{x_1}\left( {k + 1} \right) - {x_1}\left( k \right)}}{T} = {x_2}\left( k \right)} \hfill \\ {\frac{{{x_2}\left( {k + 1} \right) - {x_2}\left( k \right)}}{T} = - \frac{k}{m}{x_1}\left( k \right) - \frac{{k\alpha }}{m}x_1^3\left( k \right) - \frac{\beta }{m}{x_2}\left( k \right) + \frac{1}{m}u\left( k \right)} \hfill \\ \end{array}$ (3.21)

Esto es,

$\begin{array}{*{20}{c}} {{x_1}\left( {k + 1} \right) = {x_1}\left( k \right) + T{x_2}\left( k \right)} \hfill \\ {{x_2}\left( {k + 1} \right) = - \frac{{\,kT}}{m}\left[ {1 + \alpha x_1^2\left( k \right)} \right]{x_1}\left( k \right) + \left( {1 - \frac{{\beta T}}{m}} \right){x_2}\left( k \right) + \frac{T}{m}u\left( k \right)} \hfill \\ \end{array}$ (3.22)

Nótese que el modelo anterior es de la forma 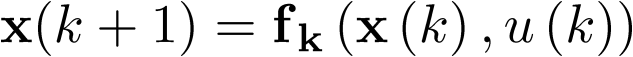${\bf{x}}\left( {k + 1} \right) = {{\bf{f}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right),u\left( k \right)} \right)$, donde fk es una función no lineal en el estado discreto 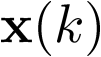${\bf{x}}\left( k \right)$; sin embargo, la ecuación de salida 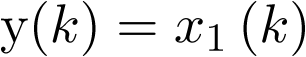$y\left( k \right) = {x_1}\left( k \right)$ es lineal.
En particular, si 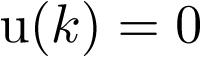$u\left( k \right) = 0$, la ecuación (3.22) se transforma en el sistema autónomo discreto no lineal 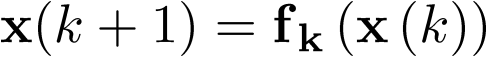${\bf{x}}\left( {k + 1} \right) = {{\bf{f}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right)} \right)$ siguiente:

$\begin{array}{*{20}{c}} {{x_1}\left( {k + 1} \right) = {x_1}\left( k \right) + T{x_2}\left( k \right)} \hfill \\ {{x_2}\left( {k + 1} \right) = - \frac{{kT\,}}{m}\left[ {1 + \alpha x_1^2\left( k \right)} \right]{x_1}\left( k \right) + \left( {1 - \frac{{\beta T}}{m}} \right){x_2}\left( k \right)} \hfill \\ \end{array}$ (2.23)

Nótese que el paso de (3.19) a (3.23) no es inmediato Por último, desestimando el término no lineal 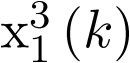$x_1^3\left( k \right)$ en (3.22), se llega al modelo de estado lineal