Principal › Apuntes de Automática › CAPÍTULO 3 › 3.2 Estados de equilibrio

Revisión de 3.2 Estados de equilibrio de 27 July, 2011 - 11:10

26 July, 2011 - 20:38 — joaquinm13
Versión para imprimirVersión para imprimir

Dado el sistema autónomo 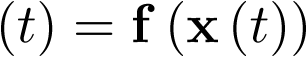${\bf{\dot x}}\left( t \right) = {\bf{f}}\left( {{\bf{x}}\left( t \right)} \right)$, se dice que el punto 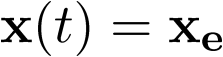${\bf{x}}\left( t \right) = {{\bf{x}}_{\bf{e}}}$ es un estado de equili-brio para dicho sistema,  si cualquier trayectoria del mismo que comience en xe permanece en dicho punto por tiempo indefinido.
De acuerdo con la definición anterior y teniendo en cuenta que los estados de equilibrio xe de un sistema pertenecen a su espacio de estado, esto es, han de ser puntos reales, el cálculo de los mismos se realiza hallando las raíces reales de la ecuación:

\[\,{\bf{\dot x}}\left( t \right) = \,{\bf{f}}\left( {{\bf{x}}\left( t \right)} \right) = {\bf{0}}\,\] (3.35)

La ecuación (3.35) puede no tener solución, que ésta sea única, varias soluciones o un continuo infinito de ellas. Obviamente, para los estados de equilibrio xe soluciones de (3.35) se cumple que

\[\,{\bf{f}}\left( {{{\bf{x}}_{\bf{e}}}\left( t \right)} \right) = {\bf{0}}\,\] (3.36)

Del mismo modo, los estados de equilibrio xe del sistema autónomo en tiempo discreto 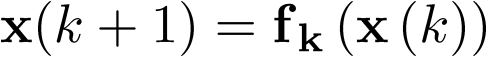${\bf{x}}\left( {k + 1} \right) = {{\bf{f}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right)} \right)$, serán aquellos que cumplan la condición

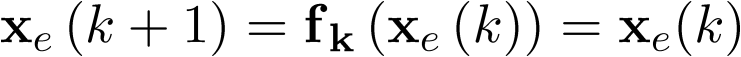${{\bf{x}}_e}\left( {k + 1} \right) = {{\bf{f}}_{\bf{k}}}\left( {{{\bf{x}}_e}\left( k \right)} \right) = {{\bf{x}}_e}(k)$ (3.37)

Ejemplo 3.2. Sistema con un único estado de equilibrio. Sea el sistema lineal muelle – masa – amortiguador del ejemplo 2.1. El estado de equilibrio en su espacio de estado se obtendrá mediante la ecuación

\[\,{\bf{\dot x}}\left( t \right) = {\bf{Ax}}\left( t \right) = {\bf{0}}\] (3.38)

la cual se escribirá para este sistema como

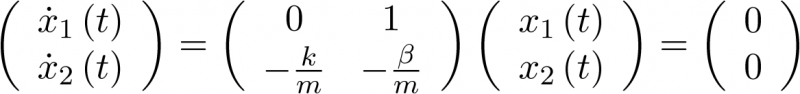$\left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 & 1 \\ { - \frac{k}{m}} & { - \frac{\beta }{m}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ \end{array}} \right)$ (3.39)

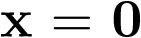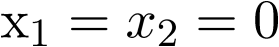La ecuación (3.38) tiene la solución única ${\bf{x}} = {\bf{0}}$ si la matriz A es no singular2. Si A es singular, entonces tiene un continuo de soluciones (un continuo de estados de equilibrio), el espacio nulo de A. En el caso que nos atañe, ecuación (3.39), se ve claramente que el sistema tiene una única solución y por tanto un único estado de equilibrio en ${x_1} = {x_2} = 0$.
Aunque este ejemplo pueda parecer trivial cabría preguntarse, ¿a partir de una condición inicial dada cualquiera, el sistema no forzado (sin entradas) va siempre al estado de equilibrio (0,0)? La pregunta se responde de forma inmediata si se conoce la evolución temporal del sistema a partir de la condición inicial, para lo cual bastaría con analizar la respuesta que ofrece la matriz de transición 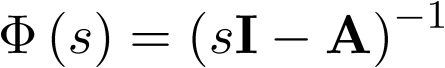${\rm{\Phi }}\left( s \right) = {\left( {s{\bf{I}} - {\bf{A}}} \right)^{ - 1}}$, ya que ésta representa el paso del sistema desde un estado inicial 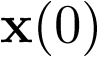${\bf{x}}\left( 0 \right)$ a otro considerado 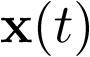${\bf{x}}\left( t \right)$ cuando la entrada es cero; esto es, caracteriza la respuesta no forzada o natural del sistema.
En el ejemplo 2.9 ya se trató este sistema en profundidad. Allí se vio cómo una matriz de transición con sus elementos formados por exponenciales negativas (2.85), origina una respuesta no forzada que lleva al sistema a su estado de equilibrio, en este caso situado en el (0,0), lo cual se comprueba gráficamente en las Figuras 2.9 y 2.10. ¿Qué provoca que las exponenciales sean negativas?, pues que el polinomio característico de la matriz de transición de un sistema continuo tenga sus raíces situadas en el eje real del semiplano izquierdo del plano complejo 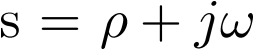$s = \rho + j\omega $, esto es, que dichas raíces (polos del sistema) sean reales y negativas (para el caso de los sistemas discretos la respuesta no forzada lleva al sistema al estado de equilibrio si el polinomio característico tiene sus raíces dentro de un círculo con centro en el origen y radio unidad)3.
El hecho de que la respuesta natural del sistema tienda a cero hace que el sistema sea estable, esto es una entrada acotada siempre produce una salida acotada, ya que el régimen transitorio desaparece con el tiempo y al final el sistema responde a la entrada de forma limitada. Véase en la ecuación (2.89) como la respuesta del sistema a una entrada es la suma de la respuesta natural que desaparece con el tiempo (por eso el sistema no forzado va a su estado de equilibrio) más la respuesta forzada, que es la que queda al final (cuando desaparece el transitorio de la respuesta natural) como respuesta estacionaria o de régimen permanente del sistema a la excitación de entrada.