A. Javier Barragán Piña

Versión para imprimir

Ejercicio error

Se desea diseñar el sistema de control de la figura, para que cumpla las siguientes especificaciones:

a) Error de estado estacionario menor del 10%, para una entrada rampa y 0 para una entrada escalón.

b) Sobre impulso máximo, menor del 5%.

c) Tiempo de asentamiento (2%), menor de 3 seg.

d) Dibujar sobre el plano “S” la región donde puedan estar ubicados los polos del sistema, para que se cumplan las especificaciones.

 

 

e_ss(2%)≤10%

Mp≤5%

ts(2%)≤3seg

 

Si tiene sobre impulso, es porque es un sistema subamortiguado. Por lo tanto:

\[G_{(s)}=\frac{K_o·{\omega n}^2}{s^2+2\delta \omega ns+{\omega n}^2}\]

Hallamos su función de transferencia:

\[G_{\left(s\right)}=\frac{Y(s)}{R(s)}=\]

\[\frac{K_1·\frac{1}{s\left(s+2\right)}}{1+K_1·\frac{1}{s\left(s+2\right)}·\left(1+K_2s\right)}=\]

\[\frac{\frac{K_1}{s\left(s+2\right)}}{\frac{s\left(s+2\right)+K_1\left(1+K_2s\right)}{s\left(s+2\right)}}=\]

\[\frac{K_1}{s\left(s+2\right)+K_1\left(1+K_2s\right)}=\]

\[\frac{K_1}{s^2+2s+K_1+K_1K_2s}=\]

\[\frac{K_1}{s^2+(2+K_1K_2)s+K_1}=\]

Comparando la primera ecuación y la última podemos obtener:

NOTA: Sólo en casos muy concretos será posible comparar la función de transferencia del sistema con la de un sistema de 2º orden. En los casos donde la comparación no sea posible, será necesario realizar el Lugar Geométrico de las Raíces y escoger unos polos de lazo cerrado que permitan el cumplimiento de las especificaciones.

\[K_1={\omega n}^2·Ko\]

\[2+K_1K_2=2\delta \omega n\]

\[{\omega n}^2=K_1\]

Por lo tanto:

\[\omega n=\sqrt{K_1}\]

\[Ko=1\]

\[2\delta \omega n=2+K_1K_2\ \to \ \]

\[\delta =\frac{2+K_1K_2}{2\omega n}\ \to \]

\[\delta =\frac{2+K_1K_2}{2\sqrt{K_1}}\]

A continuación despejamos la señal de error:

\[E_{(s)}=R_{(s)}-M_{(s)}\]

\[M_{(s)}=Y_{\left(s\right)}(1+K_2s)\]

\[Y_{(s)}=\frac{U_{(s)}}{s(s+2)}\]

\[U_{(s)}=E_{(s)}·K_1\]

 

 

\[E_{(s)}=R_{(s)}-\frac{E_{(s)}·K_1}{s(s+2)}(1+K_2s)\]

\[E_{(s)}+\frac{E_{(s)}·K_1}{s(s+2)}(1+K_2s)=R_{(s)}\]

\[E_{\left(s\right)}(1+\frac{K_1}{s\left(s+2\right)}\left(1+K_2s\right))=R_{(s)}\]

\[E_{\left(s\right)}=\frac{R_{(s)}}{1+\frac{K_1}{s(s+2)}(1+K_2s)}\]

Aplicamos El teorema del valor final: (para la señal de error $E_{(s)}$)

\[R_{(s)}=\frac{1}{s^2}\]

\[e_{ss}={\mathop{\lim }_{s\to 0} s·\ }E_{(s)}=\]

\[{\mathop{\lim }_{s\to 0} s·\ }\frac{R_{(s)}}{1+\frac{K_1}{s(s+2)}(1+K_2s)}=\]

\[{\mathop{\lim }_{s\to 0} s·\ }\frac{1}{s^2}\frac{1}{1+\frac{K_1(1+K_2s)}{s(s+2)}}=\]

\[{\mathop{\lim }_{s\to 0} \frac{1}{s+\frac{{sK}_1(1+K_2s)}{s(s+2)}}=\ }\]

\[\frac{1}{0+\frac{K_1+K_1K_20}{0+2}}=\frac{1}{\frac{K_1}{2}}=\frac{2}{K_1}\]

Igualamos las ecuaciones del error para despejar K1:

\[e_{ss}\le 10\%=0.1\]

\[0.1\ge \frac{2}{K_1}\ \ \to \ \ K_1\ge 20\]

Igualamos las ecuaciones del sobreimpulso para calcular el delta:

\[Mp=e^{\frac{-\delta ·\pi }{\sqrt{1-{\delta }^2}}}\]

\[Mp\le 5\%=0.05\]

\[0.05=e^{\frac{-\delta ·\pi }{\sqrt{1-{\delta }^2}}}\ \ \ \to \ \ \ \ \ \]

\[{(ln\ 0.05)}^2={\left(\frac{-\delta ·\pi }{\sqrt{1-{\delta }^2}}\right)}^2\ \ \to \]

\[8.97=\frac{-\delta ·\pi }{1-{\delta }^2}\ \ \ \to \]

 

[8.97-8.97·{\delta }^2={\delta }^2{\pi }^2\ \ \ \to \ \ \ \ \ \ \]

 

[8.97={\delta }^2·{\pi }^2+8.97{\delta }^2\ \ \ \to \]

 

\[\frac{8.97}{{\pi }^2+8.97}={\delta }^2\]

 

\[\delta =\sqrt{\frac{8.97}{{\pi }^2+8.97}}\ \ \ \to \ \ \ \delta \ge 0.69\]

 

Igualamos las ecuaciones del tiempo de asentamiento:

 

\[{ts}_{\left(2\%\right)}\le 3seg.\]

 

\[{ts}_{\left(2\%\right)}=\frac{4}{\delta \omega n}\]

 

\[\frac{4}{\delta \omega n}\le 3\ \ \ \to \ \ \ 4\le 3\delta \omega n\ \ \ \to \ \ \ \frac{4}{3}\le \delta \omega n\]

 

\[\omega n=\sqrt{K_1}\]

 

\[K_1\ge 20\]

 

\[0.69·\sqrt{20}=3.086\ \ \ \to \ \ \ 3.086\ge 3\]

 

Igualamos las ecuaciones para calcular K2:

 

\[\delta =\frac{2+K_1K_2}{2\sqrt{K_1}}\ \ \ \to \ \ \ \ \ \]

 

\[2+K_1K_2\ge 2\sqrt{K_1}·0.69\ \ \ \to \]

 

\[K_2\ge \frac{2·\sqrt{K_1}·0.69-2}{K_1}\]

 

\[K_1=20\]

 

\[\delta =0.69\]

 

\[K_2\ge \frac{2·\sqrt{20}·0.69-2}{20}\ \ \ \to \ \ \ K_2\ge 0.2086\]

 

 

Como $K_1\ge 20$, le damos por ejemplo el valor de 30:

 

Igualamos las ecuaciones para calcular delta:

 

\[K_2=0.2086\]

 

\[K_1=30\]

 

 

\[K_2\ge \frac{2·\sqrt{K_1}·\delta -2}{K_1}\ \ \ \to \ \ \ \]

 

\[\ \ \frac{K_2·K_1+2}{2·\sqrt{K_1}}\ge \delta \ \ \ \to \]

 

\[\frac{0.2086·30+2}{2·\sqrt{30}}\ge \delta \ \ \ \to \ \ \ \delta \le 0.75\]

 

 

Igualamos las ecuaciones para calcular el sobreimpulso:

\[Mp=e^{\frac{-\delta ·\pi }{\sqrt{1-{\delta }^2}}}\ \ \ \to \ \ \]

 

\[Mp=e^{\frac{-0.75·\pi }{\sqrt{1-{0.75}^2}}}\ \ \ \ \to \ \ \ Mp=0.028=2.8\%\]

 

 

\[\delta \le 0.75\]

 

 

Igualamos ecuaciones para calcular el error:

\[e_{ss}=\frac{2}{K_1}\ \ \ \ \to \ \ \ e_{ss}=\frac{2}{30}\ \ \ \to \ \ \ e_{ss}=0.067=6.7\%\]

 

\[K_1=30\]

 

 

Igualamos ecuaciones para calcular el tiempo de asentamiento:

\[{ts}_{\left(2\%\right)}=\frac{4}{\delta \omega n}\ \ \ \to \ \ \ {ts}_{\left(2\%\right)}=\frac{4}{0.75·\sqrt{30}}\ \ \ \to \ \ \ {ts}_{\left(2\%\right)}=0.97seg.\]

 

\[\omega n=\sqrt{K_1}=\sqrt{30}\]

 

\[\delta \le 0.75\]

 

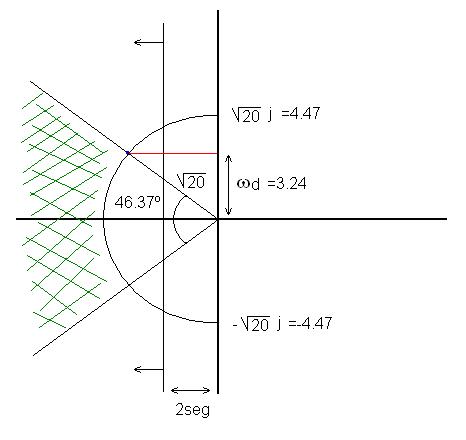
Ahora vamos a dibujar la gráfica con los datos que tenemos:

 

 

 

 

 

\[\beta =arcos\ \delta \ \ \ \to \ \ \ \beta =arcos\ 0.69=46.37º\]

 

 

\[\omega d=\sqrt{20}·\sqrt{1-{0.69}^2}\ \ \ \ \to \ \ \ \omega d=4.47·0.7238=3.24\ \ \ \to \ \ \ \sigma =\delta \omega n=\]

 

\[0.69·\sqrt{20}=3.086\]