A. Javier Barragán Piña

Versión para imprimir

PROBLEMA PROPUESTO:

Sacar la función de transferencia y estudiar los distintos sistemas de segundo orden en función del factor de amortiguamiento del siguiente circuito:

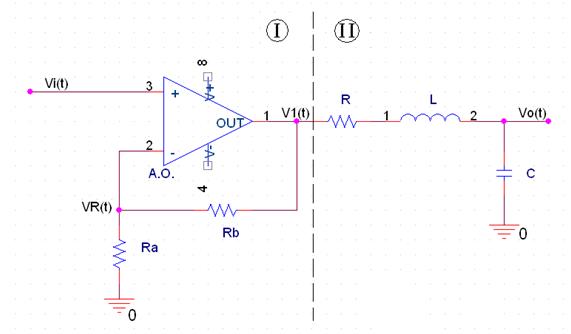
Ht(s) = H1 (s) * H2(s)

Etapa (I) Amplificador no inversor, esta etapa es la encargada de introducir ganancia en el circuito.

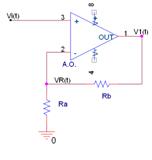
$H1(t) = \frac{{V1(t)}}{{Vi(t)}} = 1 + \frac{{Rb}}{{Ra}}$ ---> ${\rm{VR(t) = }}\frac{{{\rm{Ra}}}}{{{\rm{Ra + Rb}}}}V1(t)$

Vi(t)=VR(t)

${\rm{Vi(t) = }}\frac{{{\rm{Ra}}}}{{{\rm{Ra + Rb}}}}V1(t)$ ---> ${\rm{H1(s) = }}\frac{{V1(s)}}{{Vi(s)}} = \frac{{{\rm{Ra}}}}{{{\rm{Ra + Rb}}}} = 1 + \frac{{Rb}}{{Ra}}$

Etapa (II),circuito RLC:

------->

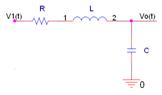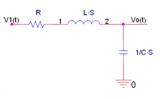
${\rm{H2(s) = }}\frac{{Vo(s)}}{{V1(s)}}$ ----> $Vo(s) = \frac{{\frac{1}{{Cs}}}}{{R + Ls + \frac{1}{{Cs}}}}V1(s)$

$Vo(s) = \frac{{\frac{1}{{Cs}}}}{{\frac{{CRs+CLs^2+1}}{{Cs}}}}V1(s)$ ----> $Vo(s) = \frac{1}{{CRs+CLs^2+1}}V1(s)$

$Vo(s) = \frac{{\frac{1}{{LC}}}}{{\frac{{Rs}}{L}+s^2+\frac{1}{{LC}}}}V1(s) $ -----> $Vo(s) = \frac{{\frac{1}{{LC}}}}{{s^2+\frac{{Rs}}{L}+\frac{1}{{LC}}}}V1(s)$

Etapa (I) y etapa (II): H t(s) = H1(s) * H2(s)

$Ht(s) = \frac{{V1(s)}}{{V1(s)}}\frac{{{\rm{Vo(s)}}}}{{{\rm{V1(s)}}}} = (\frac{{Ra}}{{Ra+Rb}})\frac{{\frac{1}{{LC}}}}{{\frac{{Rs}}{L}+s^2+\frac{{1}}{{LC}}}}$

Función transferencia de 2º orden:

$Ht(s) = \frac{{\frac{1}{{LC}}(1+\frac{{Rb}}{{Ra}})}}{{\frac{{Rs}}{L}+s^2+\frac{1}{{LC}}}}$ ------> $\approx Ht(s) =\frac{{Ko \cdot Wn^2}}{{s^2+2\cdot\delta\cdot Wn \cdot s+Wn^2 }}$

$Wn = \frac{1}{{\sqrt {LC} }}$

$ 2 \cdot \delta \cdot Wn = \frac{R}{L}\Rightarrow \delta= \frac{{\frac{R}{L}}}{{\frac{2}{{\sqrt {LC} }}}} = \frac{R}{2}\sqrt{\frac{C}{L}}$

Coeficiente de amortiguamiento: $\delta= \frac{R}{2}\sqrt{\frac{C}{L}} $

· Sistema Sobreamortiguado: $\delta > 1$ ----> $\delta=\frac{R}{2}\sqrt{\frac{C}{L}}> 1$

· Sistema Críticamente amortiguado: $\delta = 1$ ----> $\delta= \frac{R}{2}\sqrt{\frac{C}{L}} = 1$

· Sistema Subamortiguado: $ 0 < \delta < 1$ ----> $ 0 < \delta = \frac{R}{2}\sqrt{\frac{C}{L}} < 1$