A. Javier Barragán Piña

Versión para imprimir

Calcular la función de transferencia pulso de los siguientes sistemas en lazo cerrado...

- Primer sistema

$
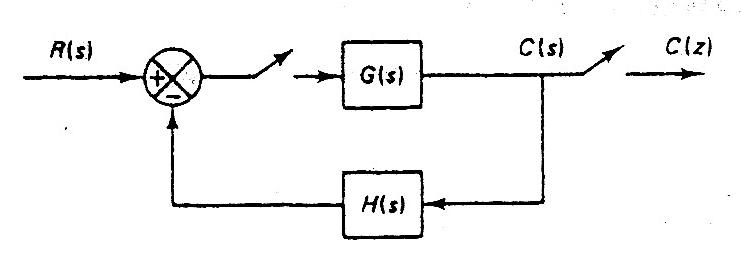
\begin{array}{l}
Y(s) = E*(s) \cdot G(s) \to Y*(s) = E*(s) \cdot G*(s) \\
E(s) = R(s) - B(s) \to E*(s) = R*(s) - B*(s) \\
B(s) = Y(s)*H(s) \to B*(s) = [Y(s) \cdot H(s)]* \\
..... \\
E*(s) = R*(s) - B*(s) \\
E*(s) = R*(s) - [Y(s) \cdot H(s)]* \\
E*(s) = R*(s) - [E*(s) \cdot G(s) \cdot H(s)]* \\
E*(s) = R*(s) - E*(s) \cdot [G(s) \cdot H(s)]* \\
E*(s) = R*(s) - E*(s) \cdot GH*(s) \\
E*(s) + E*(s) \cdot GH*(s) = R*(s) \\
E*(s) \cdot [1 + GH*(s)] = R*(s) \\
E*(s) = \frac{{R*(s)}}{{1 + GH*(s)}} \\
..... \\
Y*(s) = E*(s) \cdot G*(s) \\
Y*(s) = \frac{{R*(s)}}{{1 + GH*(s)}} \cdot G*(s) \\
Y(z) = \frac{{R(z)}}{{1 + GH(z)}} \cdot G(z) \\
\frac{{Y(z)}}{{R(z)}} = \frac{{G(z)}}{{1 + GH(z)}} \\
\end{array}
$

- Segundo sistema

$
\begin{array}{l}
E(s) = R(s) - B(s) \to E*(s) = R*(s) - B*(s) \\
Y(s) = E*(s) \cdot G(s) \to Y*(s) = E*(s) \cdot G*(s) \\
B(s) = Y*(s) \cdot H(s) \to B*(s) = Y*(s) \cdot H*(s) \\
..... \\
E*(s) = R*(s) - B*(s) \\
E*(s) = R*(s) - Y*(s) \cdot H*(s) \\
E*(s) = R*(s) - E*(s) \cdot G*(s) \cdot H*(s) \\
E*(s) + E*(s) \cdot G*(s) \cdot H*(s) = R*(s) \\
E*(s) \cdot [1 + G*(s) \cdot H*(s)] = R*(s) \\
E*(s) = \frac{{R*(s)}}{{1 + G*(s) \cdot H*(s)}} \\
..... \\
Y*(s) = E*(s) \cdot G*(s) \\
Y*(s) = \frac{{R*(s)}}{{1 + G*(s) \cdot H*(s)}} \cdot G*(s) \\
Y(z) = \frac{{R(z)}}{{1 + G(z) \cdot H(z)}} \cdot G(z) \\
\frac{{Y(z)}}{{R(z)}} = \frac{{G(z)}}{{1 + G(z) \cdot H(z)}} \\
\end{array}
$

- Tercer sistema

$
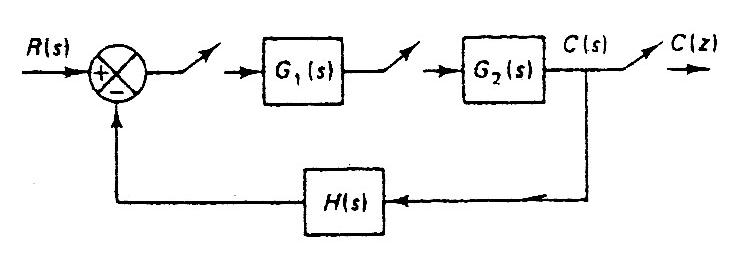
\begin{array}{l}
E(s) = R(s) - B(s) \to E*(s) = R*(s) - B*(s) \\
B(s) = Y(s) \cdot H(s) \to B*(s) = [Y(s) \cdot H(s)]* \\
Y(s) = U*(s) \cdot G_2 (s) \to Y*(s) = U*(s) \cdot G_2 *(s) \\
U(s) = E*(s) \cdot G_1 (s) \to U*(s) = E*(s) \cdot G_1 *(s) \\
..... \\
E*(s) = R*(s) - B*(s) \\
E*(s) = R*(s) - [Y(s) \cdot H(s)]* \\
E*(s) = R*(s) - [U*(s) \cdot G_2 (s) \cdot H(s)]* \\
E*(s) = R*(s) - U*(s) \cdot [G_2 (s) \cdot H(s)]* \\
E*(s) = R*(s) - U*(s) \cdot G_2 H*(s) \\
..... \\
U*(s) = E*(s) \cdot G_1 *(s) \\
U*(s) = [R*(s) - U*(s) \cdot G_2 H*(s)] \cdot G_1 *(s) \\
U*(s) = R*(s) \cdot G_1 *(s) - U*(s) \cdot G_2 H*(s) \cdot G_1 *(s) \\
U*(s) + U*(s) \cdot G_2 H*(s) \cdot G_1 *(s) = R*(s) \cdot G_1 *(s) \\
U*(s) \cdot [1 + G_2 H*(s) \cdot G_1 *(s)] = R*(s) \cdot G_1 *(s) \\
U*(s) = \frac{{R*(s) \cdot G_1 *(s)}}{{1 + G_2 H*(s) \cdot G_1 *(s)}} \\
..... \\
Y*(s) = U*(s) \cdot G_2 *(s) \\
Y*(s) = \left[ {\frac{{R*(s) \cdot G_1 *(s)}}{{1 + G_2 H*(s) \cdot G_1 *(s)}}} \right] \cdot G_2 *(s) \\
Y*(s) = \frac{{R*(s) \cdot G_1 *(s) \cdot G_2 *(s)}}{{1 + G_2 H*(s) \cdot G_1 *(s)}} \\
Y(z) = \frac{{R(z) \cdot G_1 (z) \cdot G_2 (z)}}{{1 + G_2 H(z) \cdot G_1 (z)}} \\
\frac{{Y(z)}}{{R(z)}} = \frac{{G_1 (z) \cdot G_2 (z)}}{{1 + G_2 H(z) \cdot G_1 (z)}} \\
\end{array}
$