A. Javier Barragán Piña

Versión para imprimir

Ejercicio error

Se desea diseñar el sistema de control de la figura, para que cumpla las siguientes especificaciones:

a) Error de estado estacionario menor del 10%, para una entrada rampa y 0 para una entrada escalón.

b) Sobre impulso máximo, menor del 5%.

c) Tiempo de asentamiento (2%), menor de 3 seg.

d) Dibujar sobre el plano “S” la región donde puedan estar ubicados los polos del sistema, para que se cumplan las especificaciones.

 

 

e_ss(/)≤10%

Mp≤5%

ts(2%)≤3seg

 

Si tiene sobre impulso, es porque es un sistema subamortiguado. Por lo tanto:

\[G_{(S)}=\frac{K_o·{\omega n}^2}{S^2+2\delta \omega nS+{\omega n}^2}\]

Hallamos su función de transferencia:

\[G_{\left(S\right)}=\frac{Y(s)}{R(s)}=\]

\[\frac{K_1·\frac{1}{S\left(S+2\right)}}{1+K_1·\frac{1}{s\left(s+2\right)}·\left(1+K_2S\right)}=\]

\[\frac{\frac{K_1}{S\left(S+2\right)}}{\frac{S\left(S+2\right)+K_1\left(1+K_2S\right)}{S\left(S+2\right)}}=\]

\[\frac{K_1}{S\left(S+2\right)+K_1\left(1+K_2S\right)}=\]

\[\frac{K_1}{S^2+2S+K_1+K_1K_2S}=\]

\[\frac{K_1}{S^2+(2+K_1K_2)S+K_1}=\]

 

Comparando la primera ecuación y la última podemos obtener:

\[K_1={\omega n}^2·Ko\]

\[2+K_1K_2=2\delta \omega n\]

\[{\omega n}^2=K_1\]

 

Por lo tanto:

\[\omega n=\sqrt{K_1}\]

\[Ko=1\]

\[2\delta \omega n=2+K_1K_2\ \to \ \]

\[\delta =\frac{2+K_1K_2}{2\omega n}\ \to \]

\[\delta =\frac{2+K_1K_2}{2\sqrt{K_1}}\]

 

A continuación despejamos la señal de error:

\[E_{(S)}=R_{(S)}-M_{(S)}\]

\[M_{(S)}=Y_{\left(S\right)}(1+K_2S)\]

\[Y_{(S)}=\frac{U_{(S)}}{S(S+2)}\]

\[U_{(S)}=E_{(S)}·K_1\]

 

 

\[E_{(S)}=R_{(S)}-\frac{E_{(S)}·K_1}{S(S+2)}(1+K_2S)\]

\[E_{(S)}+\frac{E_{(S)}·K_1}{S(S+2)}(1+K_2S)=R_{(S)}\]

\[E_{\left(S\right)}(1+\frac{K_1}{S\left(S+2\right)}\left(1+K_2S\right))=R_{(S)}\]

\[E_{\left(S\right)}=\frac{R_{(S)}}{1+\frac{K_1}{S(S+2)}(1+K_2S)}\]

 

 

Aplicamos El teorema del valor final:  (para la señal de error $E_{(S)}$)

 

 

\[R_{(S)}=\frac{1}{S^2}\]

\[e_{SS}={\mathop{\lim }_{S\to 0} S·\ }E_{(S)}=\]

\[{\mathop{\lim }_{S\to 0} S·\ }\frac{R_{(S)}}{1+\frac{K_1}{S(S+2)}(1+K_2S)}=\]

 

\[{\mathop{\lim }_{S\to 0} S·\ }\frac{1}{S^2}\frac{1}{1+\frac{K_1(1+K_2S)}{S(S+2)}}=\]

 

\[{\mathop{\lim }_{S\to 0} \frac{1}{S+\frac{{SK}_1(1+K_2S)}{S(S+2)}}=\ }\]

 

\[\frac{1}{0+\frac{K_1+K_1K_20}{0+2}}=\frac{1}{\frac{K_1}{2}}=\frac{2}{K_1}\]

 

Igualamos las ecuaciones del error para despejar K1:

 

\[e_{SS}\le 10\%=0.1\]

\[0.1\ge \frac{2}{K_1}\ \ \to \ \ K_1\ge 20\]

 

Igualamos las ecuaciones del sobreimpulso para calcular el delta:

\[Mp=e^{\frac{-\delta ·\pi }{\sqrt{1-{\delta }^2}}}\]

\[Mp\le 5\%=0.05\]

 

\[0.05=e^{\frac{-\delta ·\pi }{\sqrt{1-{\delta }^2}}}\ \ \ \to \ \ \ \ \ \]

 

\[{(ln\ 0.05)}^2={\left(\frac{-\delta ·\pi }{\sqrt{1-{\delta }^2}}\right)}^2\ \ \to \]

 

\[8.97=\frac{-\delta ·\pi }{1-{\delta }^2}\ \ \ \to \]

 

\[8.97-8.97·{\delta }^2={\delta }^2{\pi }^2\ \ \ \to \ \ \ \ \ \ \]

 

\[8.97={\delta }^2·{\pi }^2+8.97{\delta }^2\ \ \ \to \]

 

\[\frac{8.97}{{\pi }^2+8.97}={\delta }^2\]

 

\[\delta =\sqrt{\frac{8.97}{{\pi }^2+8.97}}\ \ \ \to \ \ \ \delta \ge 0.69\]

 

Igualamos las ecuaciones del tiempo de asentamiento:

 

\[{ts}_{\left(2\%\right)}\le 3seg.\]

 

\[{ts}_{\left(2\%\right)}=\frac{4}{\delta \omega n}\]

 

\[\frac{4}{\delta \omega n}\le 3\ \ \ \to \ \ \ 4\le 3\delta \omega n\ \ \ \to \ \ \ \frac{4}{3}\le \delta \omega n\]

 

\[\omega n=\sqrt{K_1}\]

 

\[K_1\ge 20\]

 

\[0.69·\sqrt{20}=3.086\ \ \ \to \ \ \ 3.086\ge 3\]

 

Igualamos las ecuaciones para calcular K2:

 

\[\delta =\frac{2+K_1K_2}{2\sqrt{K_1}}\ \ \ \to \ \ \ \ \ \]

 

\[2+K_1K_2\ge 2\sqrt{K_1}·0.69\ \ \ \to \]

 

\[K_2\ge \frac{2·\sqrt{K_1}·0.69-2}{K_1}\]

 

\[K_1=20\]

 

\[\delta =0.69\]

 

\[K_2\ge \frac{2·\sqrt{20}·0.69-2}{20}\ \ \ \to \ \ \ K_2\ge 0.2086\]

 

 

Como $K_1\ge 20$, le damos por ejemplo el valor de 30:

 

Igualamos las ecuaciones para calcular delta:

 

\[K_2=0.2086\]

 

\[K_1=30\]

 

 

\[K_2\ge \frac{2·\sqrt{K_1}·\delta -2}{K_1}\ \ \ \to \ \ \ \]

 

\[\ \ \frac{K_2·K_1+2}{2·\sqrt{K_1}}\ge \delta \ \ \ \to \]

 

\[\frac{0.2086·30+2}{2·\sqrt{30}}\ge \delta \ \ \ \to \ \ \ \delta \le 0.75\]

 

 

Igualamos las ecuaciones para calcular el sobreimpulso:

\[Mp=e^{\frac{-\delta ·\pi }{\sqrt{1-{\delta }^2}}}\ \ \ \to \ \ \]

 

\[Mp=e^{\frac{-0.75·\pi }{\sqrt{1-{0.75}^2}}}\ \ \ \ \to \ \ \ Mp=0.028=2.8\%\]

 

 

\[\delta \le 0.75\]

 

 

Igualamos ecuaciones para calcular el error:

\[e_{ss}=\frac{2}{K_1}\ \ \ \ \to \ \ \ e_{ss}=\frac{2}{30}\ \ \ \to \ \ \ e_{ss}=0.067=6.7\%\]

 

\[K_1=30\]

 

 

Igualamos ecuaciones para calcular el tiempo de asentamiento:

\[{ts}_{\left(2\%\right)}=\frac{4}{\delta \omega n}\ \ \ \to \ \ \ {ts}_{\left(2\%\right)}=\frac{4}{0.75·\sqrt{30}}\ \ \ \to \ \ \ {ts}_{\left(2\%\right)}=0.97seg.\]

 

\[\omega n=\sqrt{K_1}=\sqrt{30}\]

 

\[\delta \le 0.75\]

 

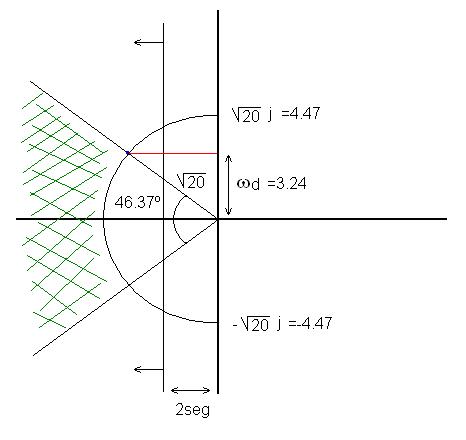
Ahora vamos a dibujar la gráfica con los datos que tenemos:

 

 

 

 

 

\[\beta =arcos\ \delta \ \ \ \to \ \ \ \beta =arcos\ 0.69=46.37º\]

 

 

\[\omega d=\sqrt{20}·\sqrt{1-{0.69}^2}\ \ \ \ \to \ \ \ \omega d=4.47·0.7238=3.24\ \ \ \to \ \ \ \sigma =\delta \omega n=\]

 

\[0.69·\sqrt{20}=3.086\]