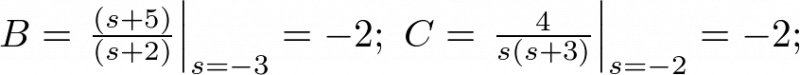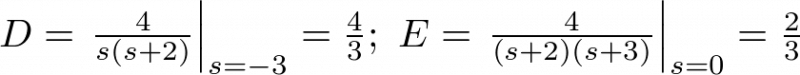Principal › Apuntes de Automática › CAPÍTULO 2 › 2.3 Función de transferencia de la ecuación de estado

Revisión de 2.3 Función de transferencia de la ecuación de estado de 1 June, 2011 - 13:14

30 May, 2011 - 19:54 — joaquinm13
Versión para imprimirVersión para imprimir
Figura 2.5.  Sistema de una entrada – una salida (SISO).

La función de transferencia de un sistema lineal e invariante en el tiempo se define como la relación entre la transformada de Laplace9 de la variable de salida y la transformada de Laplace de la variable de entrada, suponiendo que todas las condiciones iniciales se hacen iguales a cero. Esta forma de representar sistemas se denomina representación externa, ya que atiende a las señales presentes en sus terminales de entrada y salida. Así, dado el sistema de la Figura 2.5,  su función de transferencia será:

$G\left( s \right) = {\left. {\frac{{L\left[ {y\left( t \right)} \right]}}{{L\left[ {u\left( t \right)} \right]}}} \right|_{\scriptstyle {\rm{Cond}}{\rm{.}}\,{\rm{iniciales}} \hfill \atop \scriptstyle {\rm{nulas}} \hfill}} = \frac{{Y\left( s \right)}}{{U\left( s \right)}}$ (2.38)
Figura 2.6. Esquema conceptual del proceso de resolución de una ecuación diferencial mediante la transformada de Laplace.

Tradicionalmente la transformada de Laplace ha sido muy usada en sistemas de control y aún hoy día todavía lo es, sin embargo, restringe mucho el campo de aplicación, ya que sólo es apropiada para estudiar sistemas lineales y, dentro de éstos, los de una entrada-una salida o SISO (del inglés Single Imput-Single Output). Para el caso de sistemas lineales MIMO (del inglés Multiple Imputs-Multiple Outputs), habrá tantas funciones de transferencia como relaciones salida/entrada puedan ser obtenidas. Así por ejemplo, un sistema lineal con dos entradas y dos salidas generará 4 funciones de transferencia: Y1(s)/U1(s), Y1(s)/U2(s), Y2(s)/U1(s), e Y2(s)/U2(s). Evidentemente, la clave para poder hacer esta separación entrada/salida es la imposición de linealidad del sistema, la cual permite obtener la respuesta total como la suma de las respuestas individuales entre cada entrada y salida.
A continuación, con objeto de fijar ideas y familiarizar al lector no avezado en el uso operacional de la transformada de Laplace, vamos a realizar un par de ejemplos donde se pone de manifiesto su utilidad. Las ocasiones en las que se use la transformada de Laplace en el texto se hará siempre como herramienta, por tanto, se recomienda el manejo de otros libros para profundizar en este instrumento matemático.

Ejemplo 2.6. Resolución de una ecuación diferencial lineal ordinaria. La transformada de Laplace facilita de forma notable la resolución de ecuaciones diferenciales lineales, ya que convierte la ecuación diferencial temporal en un polinomio en s, y el proceso de integración para resolverla, en una manipulación algebraica de un polinomio cuya conversión al dominio temporal es inmediata mediante tablas. El proceso descrito se ilustra en la Figura 2.6. Para  realizar la transformación desde el dominio de la variable compleja s al dominio temporal se emplea una integral de inversión denominada transformada inversa10 de Laplace, 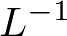${L^{ - 1}}$.
En la práctica, rara vez se emplea la integral de inversión para encontrar f(t). Hay un método más sencillo que vamos a ilustrar en este ejemplo, que consiste en descomponer la expresión en s resultante de la transformación en fracciones simples, para después, mediante tablas, realizar una traslación directa al dominio temporal. Sea pues la ecuación diferencial a resolver siguiente:

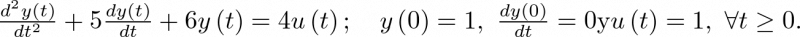$\frac{{{d^2}y\left( t \right)}}{{d{t^2}}} + 5\frac{{dy\left( t \right)}}{{dt}} + 6y\left( t \right) = 4u\left( t \right);\,\,\,\,\,\,y\left( 0 \right) = 1,\,\,\frac{{dy\left( 0 \right)}}{{dt}} = 0{\rm{ y }}u\left( t \right) = 1,\,\,\forall t \ge 0.$ (2.39)

Aplicando la transformada de Laplace11 a cada término de la ecuación:

\[L\left[ {\frac{{{d^2}y\left( t \right)}}{{d{t^2}}}} \right] + 5L\left[ {\frac{{dy\left( t \right)}}{{dt}}} \right] + 6L\left[ {y\left( t \right)} \right] = 4L\left[ {u\left( t \right)} \right]\] (2.40)

Utilizando una tabla de transformadas se escribe la correspondiente a cada sumando:

\[{s^2}Y\left( s \right) - sy\left( 0 \right) - \frac{{dy\left( 0 \right)}}{{dt}} + 5\left[ {sY\left( s \right) - y\left( 0 \right)} \right] + 6Y\left( s \right) = 4U\left( s \right)\] (2.41)

Ahora, teniendo en cuenta las condiciones iniciales y que la transformada de la señal escalón unitario U(s) es 1/s,

\[{s^2}Y\left( s \right) - s + 5\left[ {sY\left( s \right) - 1} \right] + 6Y\left( s \right) = \frac{4}{s}\] (2.42)

Agrupando términos y despejando Y(s),

\[Y\left( s \right) = \left[ {\frac{{s + 5}}{{{s^2} + 5s + 6}}} \right] + \left[ {\frac{4}{{s\left( {{s^2} + 5s + 6} \right)}}} \right]\] (2.43)

Donde . Entonces, el desarrollo en fracciones parciales12 de la expresión anterior es:

$Y\left( s \right) = \left[ {\frac{A}{{s + 2}} + \frac{B}{{s + 3}}} \right] + \left[ {\frac{C}{{s + 2}} + \frac{D}{{s + 3}} + \frac{E}{s}} \right]$ (2.44)

Cada uno de los coeficientes de la expresión anterior puede ser obtenido actuando sobre cada fracción de (2.43) y su desarrollo de (2.44) del modo siguiente:

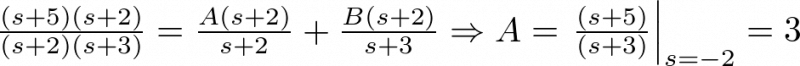$\frac{{\left( {s + 5} \right)\left( {s + 2} \right)}}{{\left( {s + 2} \right)\left( {s + 3} \right)}} = \frac{{A\left( {s + 2} \right)}}{{s + 2}} + \frac{{B\left( {s + 2} \right)}}{{s + 3}} \Rightarrow A = {\left. {\frac{{\left( {s + 5} \right)}}{{\left( {s + 3} \right)}}} \right|_{s = - 2}} = 3$ (2.45)

Del mismo modo:

$B = {\left. {\frac{{\left( {s + 5} \right)}}{{\left( {s + 2} \right)}}} \right|_{s = - 3}} = - 2;\,\,C = {\left. {\frac{4}{{s\left( {s + 3} \right)}}} \right|_{s = - 2}} = - 2;$

$D = {\left. {\frac{4}{{s\left( {s + 2} \right)}}} \right|_{s = - 3}} = \frac{4}{3};\,\,E = {\left. {\frac{4}{{\left( {s + 2} \right)\left( {s + 3} \right)}}} \right|_{s = 0}} = \frac{2}{3}$

 (2.46)

Por tanto,

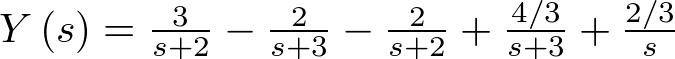$Y\left( s \right) = \frac{3}{{s + 2}} - \frac{2}{{s + 3}} - \frac{2}{{s + 2}} + \frac{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-\nulldelimiterspace} 3}}}{{s + 3}} + \frac{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}{s}$ (2.47)

Utilizando una tabla de transformadas se aplica ahora la transformada inversa13 a cada sumando para obtener la solución de la ecuación diferencial (2.39) en el dominio del tiempo:

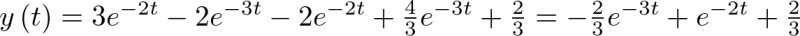$y\left( t \right) = 3{e^{ - 2t}} - 2{e^{ - 3t}} - 2{e^{ - 2t}} + \frac{4}{3}{e^{ - 3t}} + \frac{2}{3} = - \frac{2}{3}{e^{ - 3t}} + {e^{ - 2t}} + \frac{2}{3}$ (2.48)

Nótese que conforme el tiempo transcurra los términos exponenciales tenderán a cero, de modo que la respuesta a la que tenderá el sistema (respuesta estacionaria) es 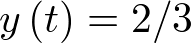$y\left( t \right) = {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}$.

Ejemplo 2.7. Sistema de amplificador operacional. Sea el sistema de amplificadores operacionales ideales de la Figura 2.7, donde se considera que las resistencias y el condensador son también ideales. Se trata de obtener la función de transferencia 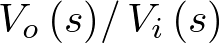${{{V_o}\left( s \right)} \mathord{\left/ {\vphantom {{{V_o}\left( s \right)} {\,{V_i}}}} \right. \kern-\nulldelimiterspace} {\,{V_i}}}\left( s \right)$.

Figura 2.7. Integrador.
Figura 2.8. Integrador. Circuito trans-formado en s.

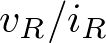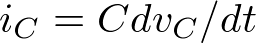Al ser las resistencias y el condensador ideales, su relación tensión/corriente está dada por ${{{v_R}} \mathord{\left/ {\vphantom {{{v_R}} {{i_R}{\rm{ }}}}} \right. \kern-\nulldelimiterspace} {{i_R}{\rm{ }}}}$ e ${i_C} = C{{d{v_C}} \mathord{\left/ {\vphantom {{d{v_C}} {dt}}} \right. \kern-\nulldelimiterspace} {dt}}$ respectivamente. Considerando la salida de estos elementos la tensión y la entrada la corriente podemos, aplicando el concepto de función de transferencia, obtener sus impedancias en el dominio de la transformada de Laplace. Esto es, \[{{{V_R}\left( s \right)} \mathord{\left/ {\vphantom {{{V_R}\left( s \right)} {{I_R}\left( s \right)}}} \right. \kern-\nulldelimiterspace} {{I_R}\left( s \right)}} = R{\rm{ y }}{{{V_C}\left( s \right)} \mathord{\left/ {\vphantom {{{V_C}\left( s \right)} {{I_C}\left( s \right)}}} \right. \kern-\nulldelimiterspace} {{I_C}\left( s \right)}} = {1 \mathord{\left/ {\vphantom {1 {Cs}}} \right. \kern-\nulldelimiterspace} {Cs}}\].
A partir de aquí, el circuito de la Figura 2.7 puede ser escrito en el dominio de la variable compleja s tal como en la Figura 2.8. Al ser los amplificadores operacionales ideales: 1) se considera el cortocircuito virtual a su entrada, con lo cual la entrada inversora está al potencial de referencia, y 2) la impedancia de entrada es infinita, de modo que sólo circula corriente por el lazo de realimentación. Bajo estas premisas se tiene que

\[\frac{{{V_i}\left( s \right)}}{{{R_1}}} = - \frac{{{V_a}\left( s \right)}}{{{1 \mathord{\left/ {\vphantom {1 {Cs}}} \right. \kern-\nulldelimiterspace} {Cs}}}}{\rm{ y }}\frac{{{V_a}\left( s \right)}}{{{R_2}}} = - \frac{{{V_o}\left( s \right)}}{{{R_3}}}\] (2.49)

Sustituyendo en la primera ecuación anterior el valor de Va(s) de la segunda, se tiene la función de transferencia buscada:

\[\frac{{{V_o}\left( s \right)}}{{{V_i}\left( s \right)}} = \frac{{{R_3}}}{{{R_2}}}\frac{1}{{{R_1}Cs}}\] (2.50)

El circuito de la figura 2.7 se denomina integrador porque la señal de salida es la integral de la de la entrada multiplicada por una constante. Esto es:

${V_o}\left( s \right) = \frac{{{R_3}}}{{{R_2}}}\frac{1}{{{R_1}Cs}}{V_i}\left( s \right);\,\,{\rm{pero }}L\left[ {\int_0^t {f\left( t \right)} dt} \right] = \frac{{F\left( s \right)}}{s}.{\rm{ Por tanto}}{\rm{, }}{L^{ - 1}}\left[ {{V_o}\left( s \right)} \right] = \frac{{{R_3}}}{{{R_1}{R_2}C}}\int_0^t {{v_i}\left( t \right)} \,dt$ (2.51)

Obtención de la función de transferencia a partir del modelo de estado

Realizados los ejemplos volvamos pues con el objeto de esta sección: obtener la función de transferencia de un sistema de una única entrada y una única salida (SISO) definido por su modelo de estado. Sea éste:

\[\begin{array}{l} {\bf{\dot x}} = {\bf{Ax}} + {\bf{B}}u \\ y = {\bf{Cx}} + {\bf{D}}u \\ \end{array}\] (2.52)

Aplicando la transformada de Laplace a la ecuación de estado y a la ecuación de salida anteriores, se tiene que

\[\begin{array}{l} s{\bf{X}}\left( s \right) = {\bf{AX}}\left( s \right) + {\bf{B}}U\left( s \right) \\ Y\left( s \right) = {\bf{CX}}\left( s \right) + {\bf{D}}U\left( s \right) \\ \end{array}\] (2.53)

Donde B es una matriz de orden nx1 debido a que el sistema tiene una única entrada u. Obsérvese que no se tienen en cuenta las condiciones iniciales, ya que lo que se busca es una función de transferencia. Reordenando la ecuación de estado anterior se obtiene que

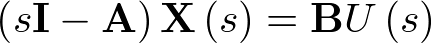$\left( {s{\bf{I}} - {\bf{A}}} \right){\bf{X}}\left( s \right) = {\bf{B}}U\left( s \right)$ (2.54)

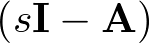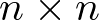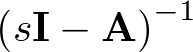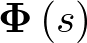Asumiendo la invertibilidad de la matriz $\left( {s{\bf{I}} - {\bf{A}}} \right)$ de orden $n \times n$, y denominando su inversa ${\left( {s{\bf{I}} - {\bf{A}}} \right)^{ - 1}}$ como ${\bf{\Phi }}\left( s \right)$, se tiene

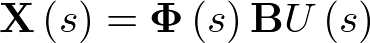${\bf{X}}\left( s \right) = {\bf{\Phi }}\left( s \right){\bf{B}}U\left( s \right)$ (2.55)

Sustituyendo ahora el valor de X(s) obtenido en la ecuación de salida (2.53), se obtiene

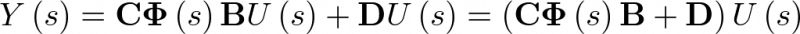$Y\left( s \right) = {\bf{C\Phi }}\left( s \right){\bf{B}}U\left( s \right) + {\bf{D}}U\left( s \right) = \left( {{\bf{C\Phi }}\left( s \right){\bf{B}} + {\bf{D}}} \right)U\left( s \right)$ (2.56)

Por consiguiente, la función de transferencia del sistema 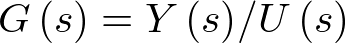$G\left( s \right) = {{Y\left( s \right)} \mathord{\left/ {\vphantom {{Y\left( s \right)} {U\left( s \right)}}} \right. \kern-\nulldelimiterspace} {U\left( s \right)}}$ es

\[G\left( s \right) = {\bf{C\Phi }}\left( s \right){\bf{B}} + {\bf{D}}\] (2.57)

Puesto que

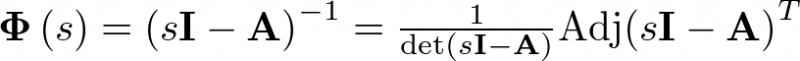${\bf{\Phi }}\left( s \right) = {\left( {s{\bf{I}} - {\bf{A}}} \right)^{ - 1}} = \frac{1}{{{\rm{det}}\left( {s{\bf{I}} - {\bf{A}}} \right)}}{\rm{Adj}}{\left( {s{\bf{I}} - {\bf{A}}} \right)^T}$ (2.58)

Queda claro que el polinomio denominador de la función de transferencia es 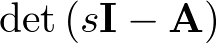${\rm{det}}\left( {s{\bf{I}} - {\bf{A}}} \right)$. Esto es, los polos14 del sistema coinciden con los valores propios o autovalores de la matriz A, ya que se obtienen a partir de su ecuación característica o polinomio característico. En conclusión, los polos del sistema dependen sólo de la matriz A, mientras que los ceros15 dependen de las matrices A, B, C y D.
Llegados a este punto cabría preguntarse por la utilidad de la expresión (2.57);  la respuesta es inmediata: permite obtener de forma directa la función de transferencia de un modelo de estado lineal de una entrada y una salida (SISO).

Comentario: Desde el punto de vista de los autores, si bien el concepto de la transformada de Laplace es de mucha utilidad en ingeniería de control (y en general en automática), y más aún el de función de transferencia que se deriva del primero, se ha preferido introducir los conceptos en el texto desde lo general a lo particular. Así, mientras el modelo de estado descrito por la expresión (2.8) es absolutamente genera (no lineal y MIMO); el modelo de estado que posibilita la aplicación de la expresión (2.57) es bastante más restrictivo (lineal y SISO).

Una vez sentadas las bases de los ámbitos de uso de las expresiones deducidas, se realizará un ejemplo de aplicación de la expresión (2.57).