Inicie su sesión para modificar los apuntes, usar los foros, etc. Si no es usuario de la web, regístrese.
2.6 Función de transferencia en tiempo discreto
El análisis de los sistemas lineales discretos se ve facilitado por el uso de una herramienta matemática denominada transformada ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) , la cual se define a partir de una secuencia de números
, la cual se define a partir de una secuencia de números 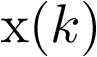 del modo siguiente:
del modo siguiente:
![${\rm{Z}}\left[ {x\left( k \right)} \right] = X\left( z \right) = \sum\limits_{k = 0}^\infty {x\left( k \right)} \,{z^{ - k}}$](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-3%282.121%29.png) |
(2.121) |
La ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) transformada definida por la ecuación anterior se denomina unilateral, ya que se considera que
transformada definida por la ecuación anterior se denomina unilateral, ya que se considera que 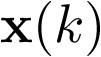 sólo está definido para
sólo está definido para 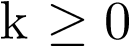 ; para el caso que esté definido desde
; para el caso que esté definido desde  , se sustituye el índice inferior de la sumatoria de (2.120) por este valor y la transformada
, se sustituye el índice inferior de la sumatoria de (2.120) por este valor y la transformada ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) es denominada bilateral. La transformada
es denominada bilateral. La transformada ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) de aplicación a sistemas de tiempo discreto guarda una gran anlogía con la transformada de Laplace de aplicación a los sistemas de tiempo continuo. Así, para condiciones iniciales nulas,
de aplicación a sistemas de tiempo discreto guarda una gran anlogía con la transformada de Laplace de aplicación a los sistemas de tiempo continuo. Así, para condiciones iniciales nulas,
![$L\left[ {{\bf{\dot x}}\left( t \right)} \right] = s\,L\left[ {{\bf{x}}\left( t \right)} \right] \Rightarrow {\rm{Z}}\left[ {{\bf{x}}\left( {k + 1} \right)} \right] = z\,{\rm{Z}}\left[ {{\bf{x}}\left( k \right)} \right]$](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-6%282.122%29.png) |
(2.122) |
Teniendo en cuenta esta correspondencia entre sistemas continuos y discretos, se pueden volver a plantear para éstos las mismas metodologías que se aplicaron a los sistemas en tiempo continuo. En concreto: 1) el concepto de función de transferencia discreta por analogía con la función de transferencia continua; 2) la solución de ecuaciones en diferencias por analogía con la solución de ecuaciones diferenciales, y 3) la obtención de la función de transferencia discreta a partir del modelo de estado discreto sin más que cambiar s por z.
En virtud de lo anterior, la función de transferencia de un sistema lineal e invariante en tiempo discreto se define como la relación entre la transformada ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) de la variable de salida y la transformada
de la variable de salida y la transformada ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) de la variable de entrada, suponiendo que todas las condiciones iniciales se hacen iguales a cero. Así, dado el sistema de la Figura 2.15, su función de transferencia será:
de la variable de entrada, suponiendo que todas las condiciones iniciales se hacen iguales a cero. Así, dado el sistema de la Figura 2.15, su función de transferencia será:
 |
| Figura 2.15. Sistema de una entrada – una salida (SISO). |
![$F\left( z \right) = {\left. {\frac{{Z\left[ {y\left( k \right)} \right]}}{{Z\left[ {u\left( k \right)} \right]}}} \right|_{\scriptstyle {\rm{Cond}}{\rm{. iniciales}} \hfill \atop \scriptstyle {\rm{nulas}} \hfill}} = \frac{{Y\left( z \right)}}{{X\left( z \right)}}$](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-8%282.123%29.png) |
(2.123) |
Aplicando la ecuación de definición de transformada ![\[{\rm{Z}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) a las señales de interés, se obtiene la expresión en el dominio z de dichas señales. Así por ejemplo, para el caso de la señal escalón unitario
a las señales de interés, se obtiene la expresión en el dominio z de dichas señales. Así por ejemplo, para el caso de la señal escalón unitario 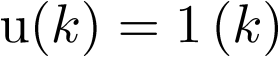 ,
,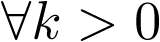 , se tendrá que aplicando (2.120),
, se tendrá que aplicando (2.120),
![$U\left( z \right) = Z\left[ {1\left( k \right)} \right] = \sum\limits_{k = 0}^\infty {1\,{z^{ - k}}} = \sum\limits_{k = 0}^\infty {{z^{ - k}} = 1 + } {z^{ - 1}} + {z^{ - 2}} + \cdots $](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-11%282.124%29.png) |
(2.124) |
Utilizando la identidad
| (2.125) |
Se tiene para 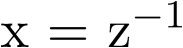 que la ecuación (2.124) puede ser escrita como
que la ecuación (2.124) puede ser escrita como
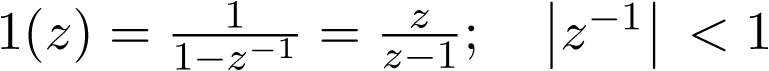 |
(2.126) |
Al igual que ocurría en el caso de la transformada de Laplace, existen tablas25 de pares de transformadas  que evitan el tedio de tener que aplicar cada vez la expresión (2.126).
que evitan el tedio de tener que aplicar cada vez la expresión (2.126).
Ejemplo 2.14. Función de transferencia de un sistema definido por una ecuación en diferencias. Sea el sistema definido por la ecuación en diferencias siguiente:
 |
(2.127) |
Del mismo modo que en el paso del tiempo continuo al dominio de la transformada de Laplace se aplicó la propiedad de diferenciación real (expresiones (2.40) a (2.41)), ahora, para pasar del tiempo discreto al dominio de la transformada 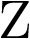 se aplica la propiedad de traslación real en el tiempo:
se aplica la propiedad de traslación real en el tiempo:
|
|
(2.128) |
Esto permite transformar la ecuación en diferencias (2.126) en la expresión
![\[X\left( z \right) + 3{z^{ - 1}}X\left( z \right) + 3{z^{ - 2}}X\left( z \right) + {z^{ - 3}}X\left( z \right) = {z^{ - 2}}U\left( z \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-17%281.129%29.png) |
(2.129) |
De aquí,
![\[\frac{{X\left( z \right)}}{{U\left( z \right)}} = \frac{{{z^{ - 2}}}}{{1 + 3{z^{ - 1}} + 3{z^{ - 2}} + {z^{ - 3}}}} = \frac{z}{{{z^3} + 3{z^2} + 3z + 1}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-18%281.130%29.png) |
(2.130) |
Ejemplo 2.15. Resolución de una ecuación en diferencias. Igual que la transformada de Laplace es una herramienta útil para resolver ecuaciones diferenciales lineales, la transformada 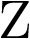 lo es para resolver ecuaciones en diferencias lineales. Dada pues la ecuación en diferencias (2.130), se trata de obtener la solución
lo es para resolver ecuaciones en diferencias lineales. Dada pues la ecuación en diferencias (2.130), se trata de obtener la solución 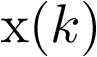 para las condiciones:
para las condiciones: ![\[u\left( 0 \right) = u\left( 1 \right) = 1\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-19.png) ;
; 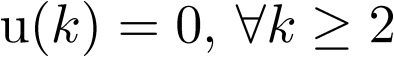 y
y 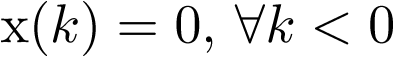 .
.
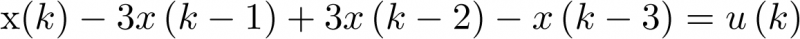 |
(2.131) |
La transformada 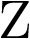 del primer miembro de la ecuación anterior se obtiene como en el ejemplo precedente. Respecto de la transformada
del primer miembro de la ecuación anterior se obtiene como en el ejemplo precedente. Respecto de la transformada 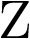 de la entrada, aplicando la definición de transformada
de la entrada, aplicando la definición de transformada 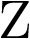 , (2.120):
, (2.120):
![\[Z\left[ {u\left( k \right)} \right] = U\left( z \right) = \sum\limits_{k = 0}^\infty {u\left( k \right)} \,{z^{ - k}} = u\left( 0 \right){z^0} + u\left( 1 \right){z^{ - 1}} + u\left( 2 \right){z^{ - 2}} + \cdots = 1 + {z^{ - 1}} = \frac{{z + 1}}{z}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-23%282.132%29.png) |
(2.132) |
La transformada ![\[Z\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-1.png) de (2.130) puede ser ya escrita como
de (2.130) puede ser ya escrita como
![\[X\left( z \right)\left[ {1 - 3{z^{ - 1}} + 3{z^{ - 2}} - {z^{ - 3}}} \right] = \frac{{z + 1}}{z} \Rightarrow \frac{{X\left( z \right)}}{z} = \frac{{{z^2} + z}}{{{z^3} - 3{z^2} + 3z - 1}} = \frac{{{z^2} + z}}{{{{\left( {z - 1} \right)}^3}}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-24%282.133%29.png) |
(2.133) |
Un poco más adelante se verá por qué interesa despejar la variable a calcular dividida por z. Ahora, al igual que se procedía para la transformada de Laplace, se descompone la relación de polinomios en fracciones simples. Nótese que la raíz del denominador (polo) es de multiplicidad 3.
![\[\frac{{X\left( z \right)}}{z} = \frac{{{z^2} + z}}{{{{\left( {z - 1} \right)}^3}}} = \frac{A}{{z - 1}} + \frac{B}{{{{\left( {z - 1} \right)}^2}}} + \frac{C}{{{{\left( {z - 1} \right)}^3}}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-25%282.134%29.png) |
(2.134) |
Para el cálculo de C se puede proceder como en el caso cuando no hay polos múltiples, esto es, multiplicando ambos miembros de esta última ecuación por 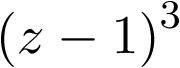 se tiene que
se tiene que
![\[{\left( {z - 1} \right)^3}\frac{{{z^2} + z}}{{{{\left( {z - 1} \right)}^3}}} = A{\left( {z - 1} \right)^2} + B\left( {z - 1} \right) + C\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-27%282.135%29.png) |
(2.135) |
A partir de aquí basta con sustituir el valor del polo para calcular C:
![\[C = {\left. {{z^2} + z} \right|_{z = 1}} = 2\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-28%282.136%29.png) |
(2.136) |
El resto de términos no pueden ser calculados de la misma forma. Una opción que dependiendo del caso puede ser algo tediosa, es sustituir el valor calculado de C en (2.134) e identificar los términos en las potencias de z:
![\[{z^2} + z = A{\left( {z - 1} \right)^2} + B\left( {z - 1} \right) + 2 = A{z^2} - 2Az + A + Bz - B + 2\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-29%282.137%29.png) |
(2.137) |
Del término en 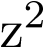 se deduce que A=1. Del término independiente,
se deduce que A=1. Del término independiente, 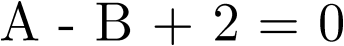 , se deduce que B=3 Al mismo resultado podríamos haber llegado de una forma más sistemática elimi-nando de forma sucesiva el índice de multiplicidad del polo, esto es, derivando cada vez respecto de z ambos miembros de (2.136):
, se deduce que B=3 Al mismo resultado podríamos haber llegado de una forma más sistemática elimi-nando de forma sucesiva el índice de multiplicidad del polo, esto es, derivando cada vez respecto de z ambos miembros de (2.136):
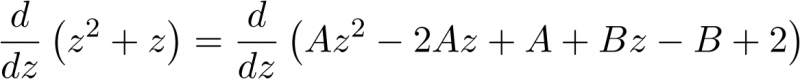 |
(2.138) |
Esto es,
![\[2z + 1 = 2A\left( {z - 1} \right) + B\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-33%282.139%29.png) |
(2.139) |
Sustituyendo en la ecuación anterior el valor del polo z=1 se tiene de nuevo que B=3 Por último, derivando ahora (2.138) respecto de z se obtiene que A=1.
En definitiva, la expresión (2.133) puede ser escrita en forma de fracciones simples del modo siguiente:
![\[\frac{{X\left( z \right)}}{z} = \frac{1}{{z - 1}} + \frac{3}{{{{\left( {z - 1} \right)}^2}}} + \frac{2}{{{{\left( {z - 1} \right)}^3}}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-34%282.140%29.png) |
(2.140) |
A partir de aquí se escribe la expresión anterior en la forma como aparecen los términos en las tablas de transformadas, esto es, en potencias de z-1,
 |
(2.141) |
Aplicando la transformada z inversa26, z-1, a la ecuación anterior sabiendo que
![\[Z\left[ {1\left( k \right)} \right] = \frac{1}{{1 - {z^{ - 1}}}}{\rm{, }}Z\left[ {kT} \right]{\rm{ = }}\frac{{T{z^{ - 1}}}}{{{{\left( {1 - {z^{ - 1}}} \right)}^2}}}{\rm{ y }}Z\left[ {\frac{{k\left( {k - 1} \right) \cdots \left( {k - m + 2} \right)}}{{\left( {m - 1} \right){\rm{!}}}}} \right] = \frac{{{z^{ - m + 1}}}}{{{{\left( {1 - {z^{ - 1}}} \right)}^m}}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-36%282.142%29.png) |
(2.142) |
Se obtiene la solución de (2.126):
![\[x\left( k \right) = 1\left( k \right) + 3k + 2\frac{{k\left( {k - 1} \right)}}{{2{\rm{!}}}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-37%282.143%29.png) |
(2.143) |
Para los primeros 3 muestreos se tiene que
![\[\begin{array}{*{20}{c}} {x\left( 0 \right) = 1\left( 0 \right) = 1} \hfill \\ {x\left( 1 \right) = 1\left( 1 \right) + 3\,.1 = 4} \hfill \\ {x\left( 2 \right) = 1\left( 2 \right) + 3\,.\,2\, + 2\frac{{2\,.1}}{{2{\rm{!}}}} = 9} \hfill \\ {x\left( 3 \right) = 1\left( 3 \right) + 3\,.\,3\, + 2\frac{{3\,.\,2}}{{2{\rm{!}}}} = 16} \hfill \\ \end{array}\,\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-38%282.144%29.png) |
(2.144) |
La ecuación en diferencias (2.126) podría haber sido resuelta también de forma iterativa como en el ejemplo 2.10, esto es:
![\[\begin{array}{*{20}{c}} {x\left( 0 \right) = u\left( 0 \right) = 1} \hfill \\ {x\left( 1 \right) = u\left( 1 \right) + 3x\left( 0 \right) = 4} \hfill \\ {x\left( 2 \right) = 3x\left( 1 \right) - 3x\left( 0 \right) = 9} \hfill \\ {x\left( 3 \right) = 3x\left( 2 \right) - 3x\left( 1 \right) + x\left( 0 \right) = 16} \hfill \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-39%282.145%29.png) |
(2.145) |
Obtención de la función de transferencia a partir del modelo de estado
Vamos a ver a continuación como la forma de obtener la función de transferencia discreta de un sistema de una única entrada y una única salida (SISO), definido por su modelo discreto de estado, es análoga al caso continuo. Sea pues el modelo discreto de estado:
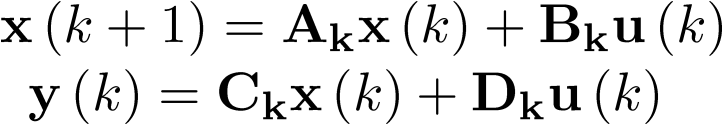 |
(2.146) |
Aplicando la transformada z (2.121) a la ecuación de estado y a la ecuación de salida anteriores, se tiene que
![\[\begin{array}{l} z{\bf{X}}\left( z \right) = {\bf{AX}}\left( z \right) + {\bf{B}}U\left( z \right) \\ Y\left( z \right) = {\bf{CX}}\left( z \right) + {\bf{D}}U\left( z \right) \\ \end{array}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-41%282.147%29.png) |
(2.147) |
Donde B es una matriz de orden nx1 debido a que el sistema tiene una única entrada u. Obsérvese que no se tienen en cuenta las condiciones iniciales, ya que lo que se busca es una función de transferencia. A partir de aquí, procediendo de forma análoga al caso continuo (ecuaciones (2.54) a (2.56)), se llega a la expresión que permite obtener de forma directa la función de transferencia de un modelo de estado discreto lineal de una entrada y una salida (SISO).
![\[G\left( z \right) = {{\bf{C}}_{\bf{k}}}{\bf{\Phi }}\left( z \right){{\bf{B}}_{\bf{k}}} + {{\bf{D}}_{\bf{k}}}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-42%282.148%29.png) |
(2.148) |
Donde
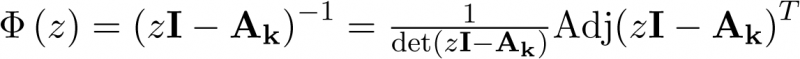 |
(2.149) |
De nuevo, como en el caso continuo, queda claro que el polinomio denominador de la función de transferencia es 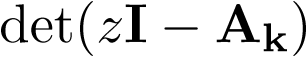 . Esto es, los polos del sistema coinciden con los valores propios o autovalores de la matriz Ak. En conclusión, los polos del sistema dependen sólo de la matriz Ak, mientras que los ceros dependen de las matrices Ak, Bk, Ck y Dk.
. Esto es, los polos del sistema coinciden con los valores propios o autovalores de la matriz Ak. En conclusión, los polos del sistema dependen sólo de la matriz Ak, mientras que los ceros dependen de las matrices Ak, Bk, Ck y Dk.
 Versión para imprimir
Versión para imprimir- Inicie sesión para enviar comentarios





![\[Z\left[ {x\left( {k + n} \right)} \right] = {z^n}\left[ {Z\left[ {x\left( k \right)} \right] - \sum\limits_{k = 0}^{n - 1} {x\left( k \right){z^{ - k}}} } \right]{\rm{ }}\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-16%281.128%29.png) y
y![\[Z\left[ {x\left( {k - n} \right)} \right] = {z^{ - n}}\,Z\left[ {x\left( k \right)} \right]\]](/antonio.barragan/files/archivos_usuarios/78/form2.6.2-16%281.128%29b.png)
