Principal › Apuntes de Automática › CAPÍTULO 2 › 2.5 Sistemas en tiempo discreto

2.5.2 Formalización

14 June, 2011 - 21:47 — joaquinm13
Versión para imprimirVersión para imprimir

En los sistemas discretos 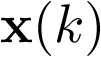${\bf{x}}\left( k \right)$ es una secuencia vectorial cuyo valor en cualquier punto de la secuencia es el estado del sistema en ese instante de tiempo discreto. También, al igual que en los sistemas continuos, el espacio de estado se define como el espacio vectorial donde toma valores el vector de estado 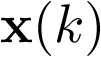${\bf{x}}\left( k \right)$. De la misma forma, teniendo en cuenta que el estado se concreta como la mínima cantidad de información (mínimo conjunto de variables) precisa para conocer la evolución del sistema para todo kT, las variables de estado en tiempo discreto son también linealmente independientes, con lo cual la dimensión del espacio de estado coincide con el número de variables de estado.
En virtud de lo anterior y por analogía con los sistemas continuos, se define como modelo de estado discreto de un sistema dinámico invariante con el tiempo, para un periodo de muestreo T dado, una relación matemática entre dos secuencias de entrada 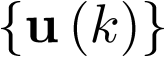$\left\{ {{\bf{u}}\left( k \right)} \right\}$ y salida 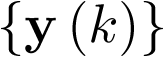$\left\{ {{\bf{y}}\left( k \right)} \right\}$ del modo siguiente:

${\bf{x}}\left( {k + 1} \right) = {{\bf{f}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right),{\bf{u}}\left( k \right)} \right),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\bf{y}}\left( k \right) = {{\bf{h}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right){\rm{,}}{\bf{u}}\left( k \right)} \right)$ (2.109)

Donde la primera ecuación en 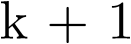$k + 1$ es la ecuación de estado, y la segunda en k es la de salida. La secuencia 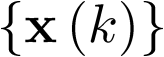$\left\{ {{\bf{x}}\left( k \right)} \right\}$ representa el vector de estado en tiempo discreto. Nótese por comparación de las ecuaciones (2.109) y (2.8) cómo para el caso discreto el modelo de estado se formula me-diante ecuaciones en diferencias, mientras que para el caso continuo se hace mediante ecuacio-nes diferenciales. 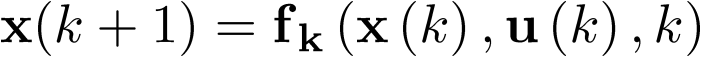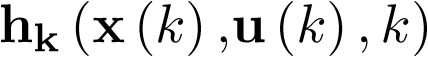Nótese también que si el sistema no fuera invariante con el tiempo (ver la primera sección del capítulo 3), las ecuaciones (2.107) deberían ser escritas como ${\bf{x}}\left( {k + 1} \right) = {{\bf{f}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right),{\bf{u}}\left( k \right),k} \right)$ e ${{\bf{h}}_{\bf{k}}}\left( {{\bf{x}}\left( k \right){\rm{,}}{\bf{u}}\left( k \right),k} \right)$.
El concepto de linealidad en los sistemas discretos es análogo al de los sistemas continuos. Esto es, un modelo de estado discreto lineal e invariante con el tiempo puede ser escrito de la forma matricial siguiente:

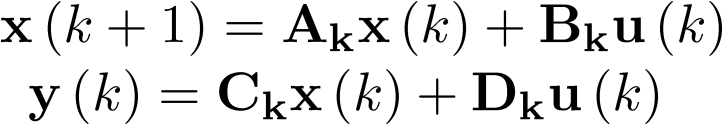$\begin{array}{*{20}{c}} {{\bf{x}}\left( {k + 1} \right) = {{\bf{A}}_{\bf{k}}}{\bf{x}}\left( k \right) + {{\bf{B}}_{\bf{k}}}{\bf{u}}\left( k \right)} \\ {{\bf{y}}\left( k \right) = {{\bf{C}}_{\bf{k}}}{\bf{x}}\left( k \right) + {{\bf{D}}_{\bf{k}}}{\bf{u}}\left( k \right)\,\,\,\,} \\ \end{array}$ (2.110)

Donde 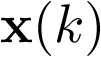${\bf{x}}\left( k \right)$ es el vector de estado en el instante k (de dimensión n), 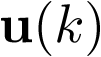${\bf{u}}\left( k \right)$ es el vector de entrada en el instante k (de dimensión p) e 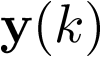${\bf{y}}\left( k \right)$ es el vector de salida en el instante k (de dimensión q). Ak, Bk, Ck y Dk son matrices constantes. 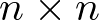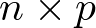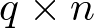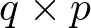La matriz Ak se denomina matriz de estado o matriz dinámica (de dimensión $n \times n$), la matriz Bk se denomina matriz de entrada o matriz de control (de dimensión $n \times p$), la matriz Ck se denomina matriz de salida o matriz sensora (de dimensión $q \times n$), y la matriz Dk se denomina matriz de transferencia directa o simplemente término directo (de dimensión $q \times p$).
Si bien la aproximación en tiempo discreto permite, como se ha visto, resolver (calcular la respuesta) sistemas lineales, éstos, la mayoría de las veces admiten solución analítica, que además es exacta. Sin embargo, los sistemas no lineales no admiten fácilmente una solución analítica, lo cual hace que su resolución se deba hacer de forma aproximada mediante métodos numéricos; en consecuencia, el método aproximado en tiempo discreto es particularmente útil para calcular la respuesta de sistemas no lineales.
Sea pues la expresión genérica de la ecuación de estado de un sistema invariante con el tiempo que puede ser no lineal:

\[\frac{{d{\bf{x}}\left( t \right)}}{{dt}} = {\bf{f}}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right)} \right)\,\] (2.111)

Si se asume que respecto del vector de control el sistema es lineal, la ecuación anterior puede ser escrita como

\[\frac{{d{\bf{x}}\left( t \right)}}{{dt}} = {\bf{f}}\left( {{\bf{x}}\left( t \right)} \right)\, + {\bf{Bu}}\left( t \right)\] (2.112)

Utilizando la aproximación de derivada en tiempo discreto dada por (2.92).

\[\frac{{{\bf{x}}\left( {t + T} \right) - {\bf{x}}\left( t \right)}}{T} = {\bf{f}}\left( {{\bf{x}}\left( t \right)} \right)\, + {\bf{Bu}}\left( t \right)\] (2.113)

La ecuación anterior puede ser escrita en el instante k (para un periodo de muestreo T) de la forma

\[\frac{{{\bf{x}}\left( {k + 1} \right) - {\bf{x}}\left( k \right)}}{T} = {\bf{f}}\left( {{\bf{x}}\left( k \right)} \right)\, + {\bf{Bu}}\left( k \right)\] (2.114)

Con lo cual, resolviendo para \[{\bf{x}}\left( {k + 1} \right)\] se tiene que

\[{\bf{x}}\left( {k + 1} \right) = {\bf{x}}\left( k \right) + T\left( {{\bf{f}}\left( {{\bf{x}}\left( k \right)} \right)\, + {\bf{Bu}}\left( k \right)} \right)\] (2.115)

Ejemplo 2.13. Respuesta de un sistema no lineal. En el ejemplo 2.2 se dedujo un modelo lineal simple para describir la propagación de una enfermedad epidémica, el cual se reproduce a continuación por comodidad.

\[\begin{array}{l} {{\dot x}_1}\left( t \right) = - \alpha {x_1}\left( t \right) - \beta {x_2}\left( t \right) + {u_1}\left( t \right) \\ {{\dot x}_2}\left( t \right) = \lambda {x_1}\left( t \right) - \gamma {x_2}\left( t \right) + {u_2}\left( t \right) \\ {{\dot x}_3}\left( t \right) = \alpha {x_1}\left( t \right) + \gamma {x_2}\left( t \right) \\ \end{array}\] (2.116)

El precio que se pagó entonces para hacer lineal el modelo y poderlo tratar en forma matricial, fue el no tener en cuenta la interacción entre las variables población en riesgo de ser infectada 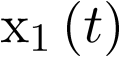${x_1}\left( t \right)$ y población infectada 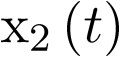${x_2}\left( t \right)$. Ahora se va a mejorar el modelo teniendo en cuenta esta interacción del modo siguiente:

\[\begin{array}{l} {{\dot x}_1}\left( t \right) = - \alpha {x_1}\left( t \right) - \beta {x_1}\left( t \right){x_2}\left( t \right) + {u_1}\left( t \right) \\ {{\dot x}_2}\left( t \right) = \beta {x_1}\left( t \right){x_2}\left( t \right) - \gamma {x_2}\left( t \right) + {u_2}\left( t \right) \\ {{\dot x}_3}\left( t \right) = \alpha {x_1}\left( t \right) + \gamma {x_2}\left( t \right) \\ \end{array}\] (2.117)

El modelo (2.116) es no lineal, por tanto no admite un tratamiento matricial como en el Ejemplo 2.12. Sean los parámetros 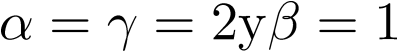$\alpha = \gamma = 2{\rm{ y }}\beta = 1$, con lo cual empleando la ecuación (2.115), el modelo (2.117) se escribirá en modo discreto de la forma

\[\begin{array}{l} {x_1}\left( {k + 1} \right) = {x_1}\left( k \right) + T\left( { - 2{x_1}\left( k \right) - {x_1}\left( k \right){x_2}\left( k \right) + {u_1}\left( k \right)} \right) \\ {x_2}\left( {k + 1} \right) = {x_2}\left( k \right) + T\left( {{x_1}\left( k \right){x_2}\left( k \right) - 2{x_2}\left( k \right) + {u_2}\left( k \right)} \right) \\ {x_3}\left( {k + 1} \right) = {x_3}\left( k \right) + 2T\left( {{x_1}\left( k \right) + {x_2}\left( k \right)} \right) \\ \end{array}\] (2.118)

Sean las condiciones iniciales 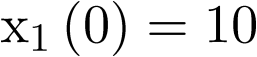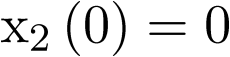${x_1}\left( 0 \right) = 10$,$\,{x_2}\left( 0 \right) = 0$ y \[{x_3}\left( 0 \right) = 0\]. Nótese que en un caso real, el valor de estas variables podría estar en cientos o miles de individuos. Del mismo modo, la medida de tiempo podría ser días o meses. 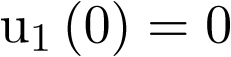Considérese ahora que en el instante inicial hay aporte de individuos a la población infectada, el cual representaremos como \[{u_2}\left( 0 \right) = 1\] (recuérdese que el significado físico de las entradas es velocidad de aporte), pero no hay aporte a la población en riesgo, con lo cual ${u_1}\left( 0 \right) = 0$. 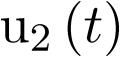Por último, asúmase que \[{u_1}\left( k \right) = 0\],\[\forall k > 0\] y que la entrada ${u_2}\left( t \right)$ decae con el tiempo hasta anularse del modo siguiente: \[{u_2}\left( 1 \right) = 0,5\]; y \[{u_2}\left( k \right) = 0\], \[\forall k > 1\]. Teniendo en cuenta pues las condiciones establecidas, la expresión general del modelo en tiempo discreto para T = 0,1 será

\[\begin{array}{l} {x_1}\left( {k + 1} \right) = 0,8\,{x_1}\left( k \right) - 0,1\,{x_1}\left( k \right){x_2}\left( k \right) \\ {x_2}\left( {k + 1} \right) = 0,8\,{x_2}\left( k \right) + 0,1\,{x_1}\left( k \right){x_2}\left( k \right) + 0,1\,{u_2}\left( k \right) \\ {x_3}\left( {k + 1} \right) = {x_3}\left( k \right) + 0,2\,{x_1}\left( k \right) + 0,2\,{x_2}\left( k \right) \\ \end{array}\] (2.119)

A partir de aquí y de modo iterativo se calcula la respuesta para cada instante de tiempo discreto k.

  (2.120)