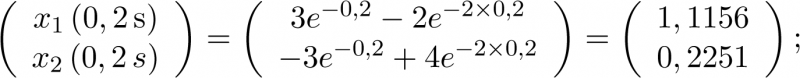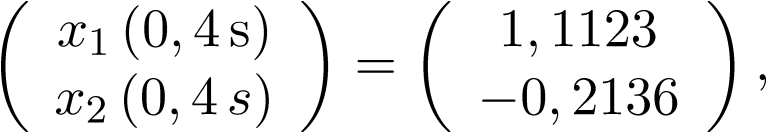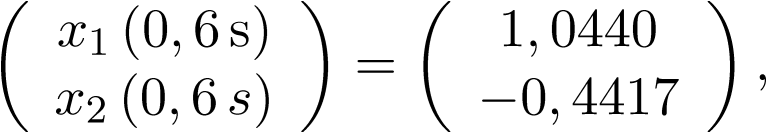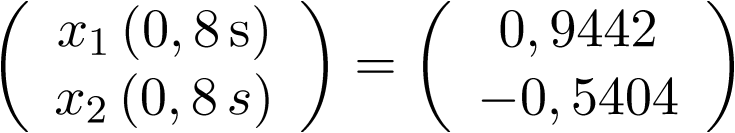2.5.1 Motivación

Figura 2.14. Definición de derivada.

Ejemplo 2.10. Solución aproximada de una ecuación diferencial ordinaria. Considérese el cálculo numérico de una ecuación diferencial ordinaria de primer orden y sea ésta, como ejemplo, la siguiente:

(2.91)

La rama de las matemáticas que soluciona este tipo de problemas es el análisis o cálculo numérico. Esta disciplina crea algoritmos que permiten resolver problemas, en los que estén involucradas cantidades numéricas, con una precisión determinada.
El análisis numérico es de aplicación cuando: 1) Los problemas no tienen solución analítica o 2) el coste de cálculo de la solución analítica es mayor que la numérica. Para la resolución de ecuaciones diferenciales ordinarias los métodos más utilizados son el método de Euler y los métodos de Runge-Kutta²².
Volviendo con el ejemplo, nótese en la Figura 2.14 que para T pequeño, puede aproximarse por la relación incremental (definición de derivada) siguiente:

(2.92)

Resolviendo la ecuación anterior para 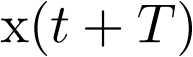$x\left( {t + T} \right)$ se tiene que

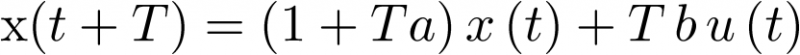$x\left( {t + T} \right) = \left( {1 + Ta} \right)x\left( t \right) + T\,b\,u\left( t \right)$

(2.93)

Evaluando esta ecuación para un tiempo discreto cualquiera t = kT se obtiene la ecuación en diferencias siguiente:

$x\left[ {\left( {k + 1} \right)T} \right] = \left( {1 + Ta} \right)x\left( {kT} \right) + T\,b\,u\left( {kT} \right)$

(2.94)

La cual, para un T dado, puede ser escrita como

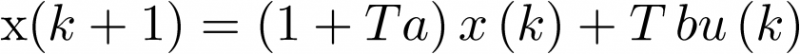$x\left( {k + 1} \right) = \left( {1 + Ta} \right)x\left( k \right) + T\,bu\left( k \right)$

(2.95)

La expresión anterior indica que el valor de la trayectoria (solución) en el instante de tiempo 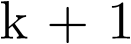$k + 1$ se calcula a partir del valor de x y de la excitación (entrada) u en el instante k.

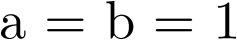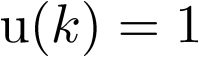La ecuación diferencial original (2.91) ha sido pues transformada por este método numérico sencillo (denominado de Euler²³) en la ecuación en diferencias (2.94). Ésta puede ser programada ahora mediante un algoritmo numérico simple en un computador. Así por ejemplo, si $a{\rm{ = }}b{\rm{ = 1}}$ , y $u\left( k \right) = 1$ para k par; 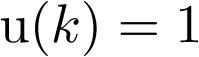${\rm{ }}u\left( k \right) = 0$ para k impar, y 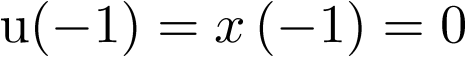$u\left( { - 1} \right) = x\left( { - 1} \right) = 0$ , se tiene que las primeras 5 muestras de 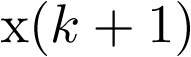$x\left( {k + 1} \right)$ valen

$\begin{array}{*{20}{c}} {x\left( 0 \right) = 2x\left( { - 1} \right) + u\left( { - 1} \right) = 0} \hfill \\ {x\left( 1 \right) = 2x\left( 0 \right) + u\left( 0 \right) = 0 + 1 = 1} \hfill \\ {x\left( 2 \right) = 2x\left( 1 \right) + u\left( 1 \right) = 2 + 0 = 2} \hfill \\ {x\left( 3 \right) = 2x\left( 2 \right) + u\left( 2 \right) = 4 + 1 = 5} \hfill \\ {x\left( 4 \right) = 2x\left( 3 \right) + u\left( 3 \right) = 10 + 0 = 10} \hfill \\ \end{array}$

(2.96)

Si se observa la ecuación (2.91), su expresión es la de un modelo de estado de orden 1 y, por ende, la ecuación (2.95) es la discretización de un modelo de estado de orden 1. Con objeto de extender lo anterior para el caso de sistemas de orden mayor que 1, se parte de la ecuación de estado lineal general que reproducimos a continuación por comodidad:

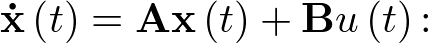${\bf{\dot x}}\left( t \right) = {\bf{Ax}}\left( t \right) + {\bf{Bu}}\left( t \right)$

(2.97)

Aplicando a esta ecuación el proceso descrito para llegar de (2.91) a (2.95), se tiene que la ecuación matricial en diferencias del modelo de estado lineal continuo estará dada por

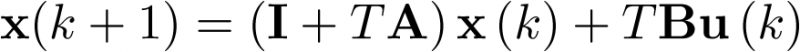${\bf{x}}\left( {k + 1} \right) = \left( {{\bf{I}} + T{\bf{A}}} \right){\bf{x}}\left( k \right) + T{\bf{Bu}}\left( k \right)$

(2.98)

Esta ecuación permite ver enseguida que la ecuación de estado discreta lineal tiene un aspecto muy similar a la de tiempo continuo. Ahora también dos matrices multiplican a los vectores de estado y de entrada igual que en el caso continuo. Respecto de la dependencia temporal de las variables, sus argumentos han sido sustituidos por el tiempo discreto k y por k + 1 para el vector de estado derivado. Esto se formalizará en la sección siguiente.

Ejemplo 2.11. Solución aproximada de un modelo de estado continuo de orden 2. Veamos una aplicación de la ecuación (2.98). Se van a calcular los primeros 4 valores discretos (iteraciones) del modelo continuo de ejemplo siguiente:

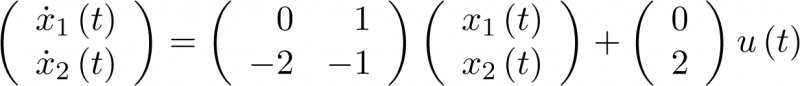$\left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} \hfill 0 & \hfill 1 \\ \hfill { - 2} & \hfill { - 1} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ 2 \\ \end{array}} \right)u\left( t \right)$

(2.99)

Supóngase que T=0,02s, en cuyo caso la aplicación de la ecuación (2.98) sobre el ejemplo proporciona la expresión siguiente:

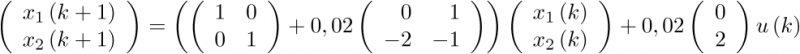$\left( {\begin{array}{*{20}{c}} {{x_1}\left( {k + 1} \right)} \\ {{x_2}\left( {k + 1} \right)} \\ \end{array}} \right) = \left( {\left( {\begin{array}{*{20}{c}} 1 & 0 \\ 0 & 1 \\ \end{array}} \right) + 0,02\left( {\begin{array}{*{20}{c}} \hfill 0 & \hfill 1 \\ \hfill { - 2} & \hfill { - 1} \\ \end{array}} \right)} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( k \right)} \\ {{x_2}\left( k \right)} \\ \end{array}} \right) + 0,02\left( {\begin{array}{*{20}{c}} 0 \\ 2 \\ \end{array}} \right)u\left( k \right)$

(2.100)

Esto es,

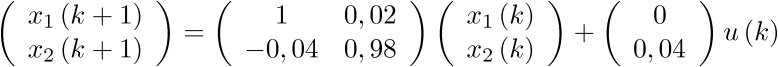$\left( {\begin{array}{*{20}{c}} {{x_1}\left( {k + 1} \right)} \\ {{x_2}\left( {k + 1} \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1 & {0,02} \\ { - 0,04} & {0,98} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( k \right)} \\ {{x_2}\left( k \right)} \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ {0,04} \\ \end{array}} \right)u\left( k \right)$

(2.101)

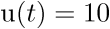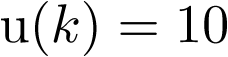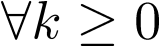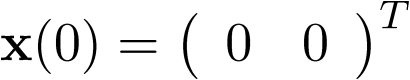Sea $u\left( t \right) = 10$ , , una señal escalón, con lo cual $u\left( k \right) = 10$ , $\forall k \ge 0$ . Sea también ${\bf{x}}\left( 0 \right) = {\left( {\begin{array}{*{20}{c}} 0 & 0 \\ \end{array}} \right)^T}$ . Entonces,

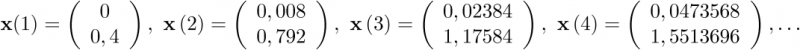${\bf{x}}\left( 1 \right) = \left( {\begin{array}{*{20}{c}} 0 \\ {0,4} \\ \end{array}} \right),\,\,{\bf{x}}\left( 2 \right) = \left( {\begin{array}{*{20}{c}} {0,008} \\ {0,792} \\ \end{array}} \right),\,\,{\bf{x}}\left( 3 \right) = \left( {\begin{array}{*{20}{c}} {{\rm{0}}{\rm{,02384}}} \\ {{\rm{1}}{\rm{,17584}}} \\ \end{array}} \right),\,\,{\bf{x}}\left( 4 \right) = \left( {\begin{array}{*{20}{c}} {{\rm{0}}{\rm{,0473568}}} \\ {{\rm{1}}{\rm{,5513696}}} \\ \end{array}} \right), \ldots$

(2.102)

Ejemplo 2.12. Respuesta temporal aproximada del sistema muelle – masa - amortiguador. En el ejemplo 2.9 se calculó la respuesta temporal exacta (analítica) de este sistema empleando la m-triz de transición de estado. Ahora se va a calcular de nuevo la respuesta temporal, pero mediante la aproximación en tiempo discreto.
El objetivo de este ejemplo es comparar la respuesta exacta del ejemplo 2.9 con la aproximada de éste; por ello es muy importante empezar a establecer una serie de pautas prácticas que permitirán obtener aproximaciones razonables.
La primera cuestión a considerar es qué periodo de muestreo elegir. Tal como se vio en la Figura 2.14, se ha de elegir un intervalo de tiempo T suficientemente pequeño de forma que la aproximación de derivada (ecuación 2.92) sea razonablemente precisa. Lógicamente, cada sistema tiene su propia dinámica y, en consecuencia, un periodo de muestreo que puede ser válido para un sistema no tiene porqué serlo para otro. Las Figuras 2.9 y 2.11 muestran la respuesta temporal del sistema objeto de análisis. Una observación mínima de las figuras no aconsejaría un tiempo de muestreo de por ejemplo T=0,2s; sin embargo, supóngase que el análisis no se ha realizado y se emplea este tiempo de muestreo, con lo cual la ecuación (2.97) es

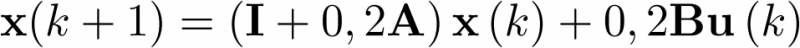${\bf{x}}\left( {k + 1} \right) = \left( {{\bf{I}} + 0,2{\bf{A}}} \right){\bf{x}}\left( k \right) + 0,2{\bf{Bu}}\left( k \right)$

(2.103)

Sustituyendo en esta ecuación los valores de las matrices A y B dadas en (2.80),

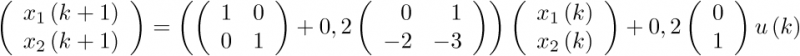$\left( {\begin{array}{*{20}{c}} {{x_1}\left( {k + 1} \right)} \\ {{x_2}\left( {k + 1} \right)} \\ \end{array}} \right) = \left( {\left( {\begin{array}{*{20}{c}} 1 & 0 \\ 0 & 1 \\ \end{array}} \right) + 0,2\left( {\begin{array}{*{20}{c}} \hfill 0 & \hfill 1 \\ \hfill { - 2} & \hfill { - 3} \\ \end{array}} \right)} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( k \right)} \\ {{x_2}\left( k \right)} \\ \end{array}} \right) + 0,2\left( {\begin{array}{*{20}{c}} 0 \\ 1 \\ \end{array}} \right)u\left( k \right)$

(2.104)

Esto es,

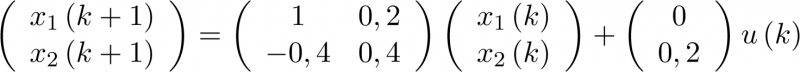$\left( {\begin{array}{*{20}{c}} {{x_1}\left( {k + 1} \right)} \\ {{x_2}\left( {k + 1} \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1 & {0,2} \\ { - 0,4} & {0,4} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( k \right)} \\ {{x_2}\left( k \right)} \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ {0,2} \\ \end{array}} \right)u\left( k \right)$

(2.105)

Ahora, con objeto de comparar la respuesta aproximada en tiempo discreto con la exacta del ejemplo 2.9, considérese la aplicación de las mismas condiciones iniciales a la ecuación (2.105), ${x_1}\left( 0 \right) = {x_2}\left( 0 \right) = 1$ y $u\left( t \right) = 0$ , en cuyo caso la primera iteración proporciona el valor siguiente:

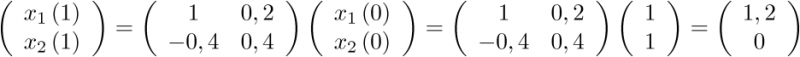$\left( {\begin{array}{*{20}{c}} {{x_1}\left( 1 \right)} \\ {{x_2}\left( 1 \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1 & {0,2} \\ { - 0,4} & {0,4} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( 0 \right)} \\ {{x_2}\left( 0 \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1 & {0,2} \\ { - 0,4} & {0,4} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1 \\ 1 \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {1,2} \\ 0 \\ \end{array}} \right)$

(2.106)

Para las tres iteraciones siguientes se obtiene que

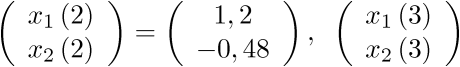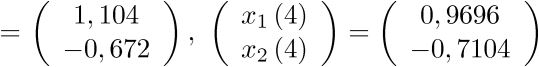$\left( {\begin{array}{*{20}{c}} {{x_1}\left( 2 \right)} \\ {{x_2}\left( 2 \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {1,2} \\ { - 0,48} \\ \end{array}} \right),\,\,{\rm{ }}\left( {\begin{array}{*{20}{c}} {{x_1}\left( 3 \right)} \\ {{x_2}\left( 3 \right)} \\ \end{array}} \right)$ $= \left( {\begin{array}{*{20}{c}} {1,104} \\ { - 0,672} \\ \end{array}} \right),\,\,\left( {\begin{array}{*{20}{c}} {{x_1}\left( 4 \right)} \\ {{x_2}\left( 4 \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {0,9696} \\ { - 0,7104} \\ \end{array}} \right)$

(2.107)

El cálculo exacto para las 4 iteraciones: 0,2 s; 0,4 s; 0,6 s y 0,8 s; se realiza mediante la expresión (2.86):

Tabla 2.1
Tiempo t	0	0,2	Error	0,4	Error	0,6	Error	0,8	Error
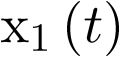${x_1}\left( t \right)$ exacto	1	1,1156	7,56%	1,1123	7,88%	1,0440	14,94%	0,9442	2,69%
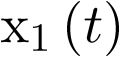${x_1}\left( t \right)$ aprox., T=0,2s	1	1,2	7,56%	1,2	7,88%	1,2	14,94%	0.9696	2,69%
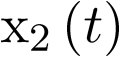${x_2}\left( t \right)$ exacto	1	0,2251	-100%	-0,2136	-124,72%	-0,4417	-52,14%	-0,5404	-31,46%
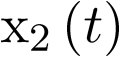${x_2}\left( t \right)$ aprox., T=0,2s	1	0	-100%	-0,48	-124,72%	-0,672	-52,14%	-0,7104	-31,46%

$\left( {\begin{array}{*{20}{c}} {{x_1}\left( {0,2\,{\rm{s}}} \right)} \\ {{x_2}\left( {0,2\,s} \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {3{e^{ - 0,2}} - 2{e^{ - 2 \times 0,2}}} \\ { - 3{e^{ - 0,2}} + 4{e^{ - 2 \times 0,2}}} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {1,1156} \\ {0,2251} \\ \end{array}} \right);$ $\,\left( {\begin{array}{*{20}{c}} {{x_1}\left( {0,4\,{\rm{s}}} \right)} \\ {{x_2}\left( {0,4\,s} \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {1,1123} \\ { - 0,2136} \\ \end{array}} \right),$
$\,\left( {\begin{array}{*{20}{c}} {{x_1}\left( {0,6\,{\rm{s}}} \right)} \\ {{x_2}\left( {0,6\,s} \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {1,0440} \\ { - 0,4417} \\ \end{array}} \right),$ $\,\left( {\begin{array}{*{20}{c}} {{x_1}\left( {0,8\,{\rm{s}}} \right)} \\ {{x_2}\left( {0,8\,s} \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {0,9442} \\ { - 0,5404} \\ \end{array}} \right)$

(2.108)

En la tabla 2.1 se resumen los resultados obtenidos junto al error cometido. Como se puede comprobar, el error cometido en ${x_2}\left( t \right)$ es muy grande. Esto se comprende fácilmente observando la Figura 2.9, ya la pendiente negativa de ${x_2}\left( t \right)$ al inicio es muy pronunciada, lo cual supone que su valor cambia mucho en 0,2 s.
Formalmente hablando, la frecuencia de muestreo²⁴ o inversa del periodo de muestreo, debe ser al menos el doble de la frecuencia más alta contenida en la señal analógica a muestrear. En la práctica es aconsejable que la frecuencia de muestreo esté comprendida entre 10 y 20 veces la de la frecuencia más alta contenida en la señal analógica a muestrear.
Si en vez del periodo de muestreo tomado se hubiera elegido uno 10 veces menor (frecuencia de muestreo 10 veces mayor), T=0,02s, el valor aproximado de ${x_2}\left( t \right)$ en la primera iteración por ejemplo, hubiera sido 0,9; y el real para t=0,02s, 0,9026. Esto es, dividiendo el periodo de muestreo por 10 el error pasa de -100% a -0,29%.

A. Javier Barragán Piña

Temas

Apuntes de Automática