Principal › Apuntes de Automática › CAPÍTULO 2 › 2.4 Matriz de transición de estado y respuesta temporal

Revisión de 2.4 Matriz de transición de estado y respuesta temporal de 1 June, 2011 - 13:58

1 June, 2011 - 13:58 — joaquinm13
Versión para imprimirVersión para imprimir

Desde el punto de vista del modelo de estado, una vez que se ha obtenido éste interesa conocer la información que proporciona, esto es, la posibilidad de analizar el comportamiento dinámico del sistema a lo largo del tiempo. Para ello se debe tener una expresión explícita de la solución o trayectoria del sistema en su espacio de estado, esto es, del vector de estado. Esta solución exige el cálculo de la ecuación de estado. Cuando ésta es no lineal, su solución puede ser muy compleja, de modo que la mayoría de las veces habrá que descartar la obtención de una expresión analítica, quedando pues la solución en el ámbito del análisis numérico realizado mediante computador. Sin embargo, cuando la ecuación de estado es lineal, bien porque el sistema lo es, o bien porque es el resultado de la linealización de un sistema no lineal, la ecuación de estado admite una solución analítica que es fácil de obtener y proporciona una información muy rica de la evolución temporal de las trayectorias (coordenadas del vector de estado) del sistema.
Sea pues la ecuación de estado en su forma lineal siguiente:

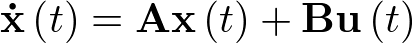${\bf{\dot x}}\left( t \right) = {\bf{Ax}}\left( t \right) + {\bf{Bu}}\left( t \right)$ (2.65)

Aplicando la transformada de Laplace con la condición inicial 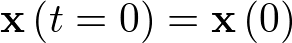${\bf{x}}\left( {t = 0} \right) = {\bf{x}}\left( 0 \right)$ se tiene que

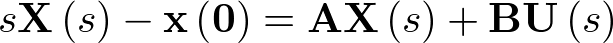$s{\bf{X}}\left( s \right) - {\bf{x}}\left( {\bf{0}} \right) = {\bf{AX}}\left( s \right) + {\bf{BU}}\left( s \right)$ (2.66)

O también

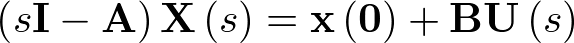$\left( {s{\bf{I}} - {\bf{A}}} \right){\bf{X}}\left( s \right) = {\bf{x}}\left( {\bf{0}} \right) + {\bf{BU}}\left( s \right)$ (2.67)

Esto es,

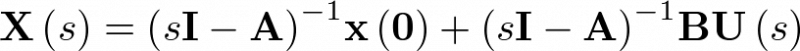${\bf{X}}\left( s \right) = {\left( {s{\bf{I}} - {\bf{A}}} \right)^{ - 1}}{\bf{x}}\left( {\bf{0}} \right) + {\left( {s{\bf{I}} - {\bf{A}}} \right)^{ - 1}}{\bf{BU}}\left( s \right)$ (2.68)