Principal › Apuntes de Automática › CAPÍTULO 2 › 2.6 Función de transferencia en tiempo discreto

Revisión de 2.6 Función de transferencia en tiempo discreto de 15 June, 2011 - 01:25

14 June, 2011 - 23:13 — joaquinm13
Versión para imprimirVersión para imprimir

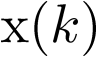El análisis de los sistemas lineales discretos se ve facilitado por el uso de una herramienta matemática denominada transformada \[{\rm{Z}}\], la cual se define a partir de una secuencia de números $x\left( k \right)$ del modo siguiente:

${\rm{Z}}\left[ {x\left( k \right)} \right] = X\left( z \right) = \sum\limits_{k = 0}^\infty {x\left( k \right)} \,{z^{ - k}}$ (2.121)

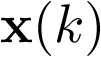La \[{\rm{Z}}\] transformada  definida por la ecuación anterior se denomina unilateral, ya que se considera que $x\left( k \right)$ sólo está definido para 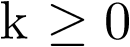$k \ge 0$; para el caso que esté definido desde $ - \infty $, se sustituye el índice inferior de la sumatoria de (2.120) por este valor y la transformada \[{\rm{Z}}\] es denominada bilateral. La transformada \[{\rm{Z}}\] de aplicación a sistemas de tiempo discreto guarda una gran anlogía con la transformada de Laplace de aplicación a los sistemas de tiempo continuo. Así, para condiciones iniciales nulas,

$L\left[ {{\bf{\dot x}}\left( t \right)} \right] = s\,L\left[ {{\bf{x}}\left( t \right)} \right] \Rightarrow {\rm{Z}}\left[ {{\bf{x}}\left( {k + 1} \right)} \right] = z\,{\rm{Z}}\left[ {{\bf{x}}\left( k \right)} \right]$ (2.122)

Teniendo en cuenta esta correspondencia entre sistemas continuos y discretos, se pueden volver a plantear para éstos las mismas metodologías que se aplicaron a los sistemas en tiempo continuo. En concreto: 1) el concepto de función de transferencia discreta por analogía con la función de transferencia continua; 2) la solución de ecuaciones en diferencias por analogía con la solu-ción de ecuaciones diferenciales, y 3)  la obtención de la función de transferencia discreta a par-tir del modelo de estado discreto sin más que cambiar s por z.
En virtud de lo anterior, la función de transferencia de un sistema lineal e invariante en tiempo discreto se define como la relación entre la transformada \[{\rm{Z}}\] de la variable de salida y la transformada \[{\rm{Z}}\] de la variable de entrada, suponiendo que todas las condiciones iniciales se hacen iguales a cero. Así, dado el sistema de la Figura 2.15,  su función de transferencia será:

Figura 2.15.  Sistema de una entrada – una salida (SISO).
$F\left( z \right) = {\left. {\frac{{Z\left[ {y\left( k \right)} \right]}}{{Z\left[ {u\left( k \right)} \right]}}} \right|_{\scriptstyle {\rm{Cond}}{\rm{. iniciales}} \hfill \atop \scriptstyle {\rm{nulas}} \hfill}} = \frac{{Y\left( z \right)}}{{X\left( z \right)}}$ (2.123)

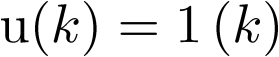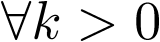Aplicando la ecuación de definición de transformada \[{\rm{Z}}\] a las señales de interés, se obtiene la expresión en el dominio z de dichas señales. Así por ejemplo, para el caso de la señal escalón unitario $u\left( k \right) = 1\left( k \right)$,$\forall k > 0$, se tendrá que aplicando (2.120),

$U\left( z \right) = Z\left[ {1\left( k \right)} \right] = \sum\limits_{k = 0}^\infty {1\,{z^{ - k}}} = \sum\limits_{k = 0}^\infty {{z^{ - k}} = 1 + } {z^{ - 1}} + {z^{ - 2}} + \cdots $ (2.124)

Utilizando la identidad

  (2.125)

Se tiene para 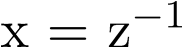$x = {z^{ - 1}}$ que la ecuación (2.124) puede ser escrita como

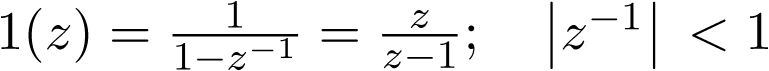$1\left( z \right) = \frac{1}{{1 - {z^{ - 1}}}} = \frac{z}{{z - 1}};\,\,\,\,\,\,\left| {{z^{ - 1}}} \right|\, < 1\,\,\,\,\,$ (2.126)

Al igual que ocurría en el caso de la transformada de Laplace, existen tablas25 de pares de transformadas 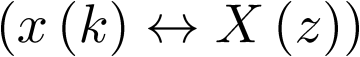$\left( {x\left( k \right) \leftrightarrow X\left( z \right)} \right)$ que evitan el tedio de tener que aplicar cada vez la expresión (2.126).

Ejemplo 2.14. Función de transferencia de un sistema definido por una ecuación en diferencias. Sea el sistema definido por la ecuación en diferencias siguiente:

$x\left( k \right) + 3x\left( {k - 1} \right) + 3x\left( {k - 2} \right) + x\left( {k - 3} \right) = u\left( {k - 2} \right)$ (2.127)

Del mismo modo que en el paso del tiempo continuo al dominio de la transformada de Laplace se aplicó la propiedad de diferenciación real (expresiones (2.40) a (2.41)),  ahora, para pasar del tiempo discreto al dominio de la transformada 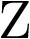$Z$ se aplica la propiedad de traslación real en el tiempo:

\[Z\left[ {x\left( {k + n} \right)} \right] = {z^n}\left[ {Z\left[ {x\left( k \right)} \right] - \sum\limits_{k = 0}^{n - 1} {x\left( k \right){z^{ - k}}} } \right]{\rm{ }}\] y
 \[Z\left[ {x\left( {k - n} \right)} \right] = {z^{ - n}}\,Z\left[ {x\left( k \right)} \right]\]

 (2.128)

Esto permite transformar la ecuación en diferencias (2.126) en la expresión

\[X\left( z \right) + 3{z^{ - 1}}X\left( z \right) + 3{z^{ - 2}}X\left( z \right) + {z^{ - 3}}X\left( z \right) = {z^{ - 2}}U\left( z \right)\] (2.129)

De aquí,

\[\frac{{X\left( z \right)}}{{U\left( z \right)}} = \frac{{{z^{ - 2}}}}{{1 + 3{z^{ - 1}} + 3{z^{ - 2}} + {z^{ - 3}}}} = \frac{z}{{{z^3} + 3{z^2} + 3z + 1}}\] (2.130)