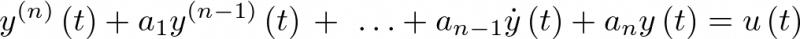Principal › Apuntes de Automática › CAPÍTULO 2 › 2.1 Modelado en el espacio de estado

2.1.2 Formalización

24 May, 2011 - 00:29 — joaquinm13
Versión para imprimirVersión para imprimir

A continuación se van a formalizar los conceptos introducidos en la sección anterior. Esto se hará para el dominio de tiempo continuo (ecuaciones diferenciales); para el dominio de tiempo discreto (ecuaciones en diferencias) se realizará en la sección 2.5.

Tiempo continuo

El estado de un sistema es una colección de variables, denominadas variables de estado, que reúnen la información suficiente sobre el pasado del mismo, de tal manera que su conocimiento en el instante actual 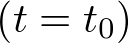$\left( {t = {t_0}} \right)$ junto con el de la entrada para el momento presente y futuro 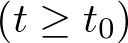$\left( {t \ge {t_0}} \right)$, permite determinar el comportamiento del sistema para cualquier $t \ge {t_0}$.
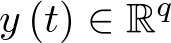Las variables de estado componen un vector \[{\mathbf{x}}\left( t \right) \in {\mathbb{R}^n}\] denominado vector de estado. Las variables de control (o de entrada) forman el vector de entrada \[{\mathbf{u}}\left( t \right) \in {\mathbb{R}^p}\], y las señales medidas (respuestas) constituyen el vector de salida $y\left( t \right) \in {\mathbb{R}^q}$. A partir de aquí, un sistema dinámico invariante con el tiempo7 puede ser representado por las ecuaciones:

(2.8)

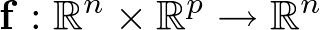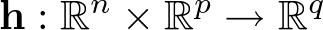Donde \[{\raise0.7ex\hbox{${d{\mathbf{x}}}$} \!\mathord{\left/ {\vphantom {{d{\mathbf{x}}} {dt}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${dt}$}}\] representa un conjunto de n ecuaciones diferenciales ordinarias. ${\mathbf{f}}:{\mathbb{R}^n} \times {\mathbb{R}^p} \to {\mathbb{R}^n}$ y ${\mathbf{h}}:{\mathbb{R}^n} \times {\mathbb{R}^p} \to {\mathbb{R}^q}$ son funciones vectoriales generalmente no lineales. Un modelo de la forma (2.8) se denomina modelo de estado. A esta forma de representar un sistema dinámico se le denomina representación interna, ya que las coordenadas de vector de estado son variables que en todo o en parte no estarán presentes en los terminales de salida del sistema.
La dimensión del vector de estado viene dada por el orden del sistema. El sistema (2.8) se denomina invariante con el tiempo porque las funciones f y h no dependen explícitamente del tiempo. Por supuesto, hay modelos más generales donde esta dependencia explícita sí se da. Como se puede apreciar en la ecuación (2.8), el modelo de estado consta de dos funciones: la función f da la variación temporal del vector de estado como una función del estado 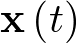${\bf{x}}\left( t \right)$ y la ley de control 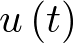${\bf{u}}\left( t \right)$ , y la función h da los valores medidos como una función del estado 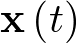${\bf{x}}\left( t \right)$ y la ley de control ${\bf{u}}\left( t \right)$.
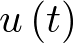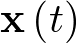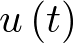Un modelo de estado se denomina lineal si las funciones f y h son lineales en ${\bf{x}}\left( t \right)$ y ${\bf{u}}\left( t \right)$ Esto permite escribir el modelo (2.8) en la forma:

$\frac{{d{\bf{x}}\left( t \right)}}{{dt}} = {\bf{Ax}}\left( t \right) + {\bf{Bu}}\left( t \right),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\bf{y}}\left( t \right) = {\bf{Cx}}\left( t \right){\rm{ + }}{\bf{Du}}\left( t \right)\,\,\,\,\,\,\,\,\,\,\,$ (2.9)

Donde A, B, C y D son matrices constantes. 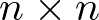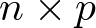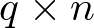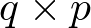La matriz A se denomina matriz de estado o matriz dinámica (de dimensión $n \times n$), la matriz B se denomina matriz de entrada o matriz de control (de dimensión $n \times p$),  la matriz C se denomina matriz de salida o matriz sensora (de dimensión $q \times n$), y la matriz D se denomina matriz de transferencia directa o simplemente término directo (de dimensión $q \times p$).
Como se ha visto, el modelo de estado se obtiene a partir de la ecuación diferencial que captura la dinámica del sistema. En consecuencia, dependiendo de la forma que tenga la ecuación dife-rencial se pueden obtener modelos de estado diferentes, los cuales, una vez conocida la metodo-logía, pueden ser obtenidos de forma directa a partir de la ecuación diferencial de partida.
Sea por ejemplo un sistema de orden n en el que la señal de control no contiene términos deri-vados:

\[\frac{{{d^n}y\left( t \right)}}{{d{t^n}}} + {a_1}\frac{{{d^{n - 1}}y\left( t \right)}}{{d{t^{n - 1}}}} + \ldots + {a_{n - 1}}\frac{{dy\left( t \right)}}{{dt}} + {a_n}y\left( t \right) = u\left( t \right),\,\,\,\,\,\]

o en notación abreviada: ${y^{\left( n \right)}}\left( t \right) + {a_1}{y^{\left( {n - 1} \right)}}\left( t \right)\, + \,\, \ldots + {a_{n - 1}}\dot y\left( t \right) + {a_n}y\left( t \right) = u\left( t \right)$

 (2.10)

Si se define

${\bf{x}}\left( t \right)\,\, = {\left[ {{x_1}\left( t \right)\,\,{x_2}\left( t \right) \ldots \,{x_n}\left( t \right)} \right]^{\rm{T}}} = \left[ {y\left( t \right)\,\,\dot y\left( t \right) \ldots {y^{\left( {n - 1} \right)}}\left( t \right)} \right]{\,^{\rm{T}}}\,\,\,\,\,\,\,$ (2.11)

Entonces, la ecuación (2.10) puede ser escrita como

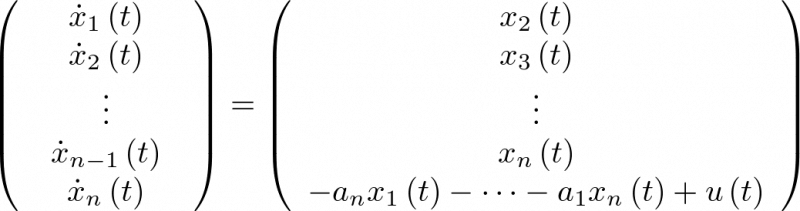$\left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ {\begin{array}{*{20}{c}} \vdots \\ {{{\dot x}_{n - 1}}\left( t \right)} \\ \end{array}} \\ {{{\dot x}_n}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{x_2}\left( t \right)} \\ {{x_3}\left( t \right)} \\ \vdots \\ {{x_n}\left( t \right)} \\ { - {a_n}{x_1}\left( t \right) - \cdots - {a_1}{x_n}\left( t \right) + u\left( t \right)} \\ \end{array}} \right)$ (2.12)

O bien en la forma 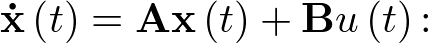${\bf{\dot x}}\left( t \right) = {\bf{Ax}}\left( t \right) + {\bf{B}}u\left( t \right){\rm{:}}$

$\left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ {\begin{array}{*{20}{c}} \vdots \\ {{{\dot x}_{n - 1}}\left( t \right)} \\ \end{array}} \\ {{{\dot x}_n}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 & 1 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ { - {a_n}} & { - {a_{n - 1}}} & \cdots & { - {a_1}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ {\begin{array}{*{20}{c}} \vdots \\ {{x_{n - 1}}\left( t \right)} \\ \end{array}} \\ {{x_n}\left( t \right)} \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ {\begin{array}{*{20}{c}} \vdots \\ 0 \\ \end{array}} \\ 1 \\ \end{array}} \right)u\left( t \right)$ (2.13)

Por último, la ecuación de salida  se escribirá:

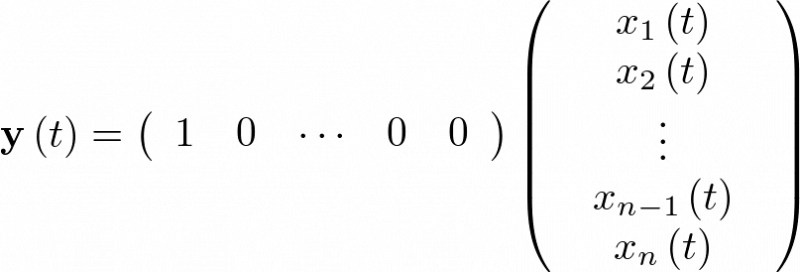${\bf{y}}\left( t \right) = \left( {\begin{array}{*{20}{c}} 1 \hfill & 0 \hfill & \cdots \hfill & 0 \hfill & 0 \hfill \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ {\begin{array}{*{20}{c}} \vdots \\ {{x_{n - 1}}\left( t \right)} \\ \end{array}} \\ {{x_n}\left( t \right)} \\ \end{array}} \right)$ (2.14)

La forma de elección de variables de estado que da lugar al modelo representado en (2.13) y (2.14) se denomina forma canónica de cadena de integradores, o forma canónica de control. Existen muchas más formas de obtener representaciones en el espacio de estado de los sistemas.  Algu-nas de ellas se irán viendo conforme sea apropiado a lo largo del texto.
Con objeto de fijar ideas vamos a realizar ahora varios ejercicios de modelado de sistemas di-námicos de diferente índole.

Ejemplo 2.2. Propagación de una enfermedad epidémica. La propagación de una enfermedad epidémica puede ser descrita mediante un conjunto de ecuaciones diferenciales de primer orden. Asúmase que el vector población de estudio 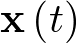${\bf{x}}\left( t \right)$ tiene 3 coordenadas: población en riesgo de ser infectada 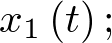${x_1}\left( t \right);$ población infectada 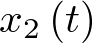${x_2}\left( t \right)$ y población que no va a ser infectada 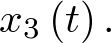${x_3}\left( t \right).$ Este último grupo reúne a las personas que son inmunes a la enfermedad, las que ya han fallecido y las que han conseguido ser aisladas para evitar contagios.
Si se asume en primera instancia que la población está aislada y el número de individuos es N, está claro que para todo t se cumplirá que 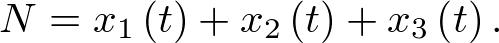$N = {x_1}\left( t \right) + {x_2}\left( t \right) + {x_3}\left( t \right).$ Con objeto de elaborar el modelo dinámico razonaremos del modo siguiente: a partir de un instante de tiempo t en el que el número de infectados es 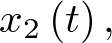${x_2}\left( t \right),$ el número de casos nuevos ocurridos en el intervalo $\left[ {t,\,\,t + \Delta t} \right]$ será ${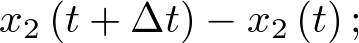x_2}\left( {t + \Delta t} \right) - {x_2}\left( t \right);$ por tanto, la evolución de cada una de las tres poblaciones será:

\[\begin{array}{l} {x_1}\left( {t + \Delta t} \right) = {x_1}\left( t \right) - \left\{ {{\rm{Excluidos hacia}}\,\,{x_3}} \right\} - \left\{ {{\rm{Excluidos hacia}}\,\,{x_2}} \right\} \\ {x_2}\left( {t + \Delta t} \right) = {x_2}\left( t \right) + \left\{ {{\rm{Contagiados desde}}\,\,{x_1}} \right\} - \left\{ {{\rm{Excluidos hacia}}\,\,{x_3}} \right\} \\ {x_3}\left( {t + \Delta t} \right) = {x_3}\left( t \right) + \left\{ {{\rm{Excluidos desde}}\,\,{x_1}} \right\} + \left\{ {{\rm{Excluidos desde}}\,\,{x_2}} \right\} \\ \end{array}\] (2.15)

Esto es,

\[\begin{array}{l} {x_1}\left( {t + \Delta t} \right) = {x_1}\left( t \right) - \alpha {x_1}\left( t \right)\Delta t - \beta {x_2}\left( t \right)\Delta t \\ {x_2}\left( {t + \Delta t} \right) = {x_2}\left( t \right) + \lambda {x_1}\left( t \right)\Delta t - \gamma {x_2}\left( t \right)\Delta t \\ {x_3}\left( {t + \Delta t} \right) = {x_3}\left( t \right) + \alpha {x_1}\left( t \right)\Delta t + \gamma {x_2}\left( t \right)\Delta t \\ \end{array}\] (2.16)

Donde los parámetros \[\alpha ,\,\beta ,\,\lambda \,\,{\rm{y}}\,\,\gamma \] son tasas, y obviamente, \[\lambda {x_1}\left( t \right)\Delta t = \beta {x_2}\left( t \right)\Delta t.\] A partir de aquí, teniendo en cuenta que:

\[{\dot x_i}\left( t \right) = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{{x_i}\left( {t + \Delta t} \right) - {x_i}\left( t \right)}}{{\Delta t}}\] (2.17)

Podemos escribir el modelo de estado del sistema que representa la propagación de la epidemia como

\[\left. \begin{array}{l} {{\dot x}_1}\left( t \right) = - \alpha {x_1}\left( t \right) - \beta {x_2}\left( t \right) \\ {{\dot x}_2}\left( t \right) = \lambda {x_1}\left( t \right) - \gamma {x_2}\left( t \right) \\ {{\dot x}_3}\left( t \right) = \alpha {x_1}\left( t \right) + \gamma {x_2}\left( t \right) \\ \end{array} \right\} \Rightarrow \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ {{{\dot x}_3}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} \hfill { - \alpha } & \hfill { - \beta } & \hfill 0 \\ \hfill \lambda & \hfill { - \gamma } & \hfill 0 \\ \hfill \alpha & \hfill \gamma & \hfill 0 \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ {{x_3}\left( t \right)} \\ \end{array}} \right)\] (2.18)


Si consideramos ahora que el sistema no está aislado, de modo que 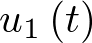${u_1}\left( t \right)$ es la velocidad con la que se incorporan nuevos individuos a la población con riesgo, y 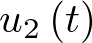${u_2}\left( t \right)$ la velocidad con la que se añaden nuevos individuos a la población infectada, la ecuación (2.18) se escribirá en la forma:

\[\left. \begin{array}{l} {{\dot x}_1}\left( t \right) = - \alpha {x_1}\left( t \right) - \beta {x_2}\left( t \right) + {u_1}\left( t \right) \\ {{\dot x}_2}\left( t \right) = \lambda {x_1}\left( t \right) - \gamma {x_2}\left( t \right) + {u_2}\left( t \right) \\ {{\dot x}_3}\left( t \right) = \alpha {x_1}\left( t \right) + \gamma {x_2}\left( t \right) \\ \end{array} \right\} \Rightarrow \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ {{{\dot x}_3}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} \hfill { - \alpha } & \hfill { - \beta } & \hfill 0 \\ \hfill \lambda & \hfill { - \gamma } & \hfill 0 \\ \hfill \alpha & \hfill \gamma & \hfill 0 \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ {{x_3}\left( t \right)} \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} \hfill 1 & \hfill 0 \\ \hfill 0 & \hfill 1 \\ \hfill 0 & \hfill 0 \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{u_1}\left( t \right)} \\ {{u_2}\left( t \right)} \\ \end{array}} \right)\] (2.19)

Nótese que los modelos (2.18) y (2.19) son simples en el sentido que son lineales, ya que no in-cluyen la interacción entre los grupos 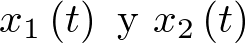${x_1}\left( t \right)\,\,{\rm{y}}\,\,{x_2}\left( t \right)$. Volveremos con esto más adelante, en el ejemplo 2.13.

Figura 2.2. Sistema péndulo.

Ejemplo 2.3. Sistema péndulo. Considere el péndulo simple de la Figura 2.2, el cual está sujeto por una cuerda inextensible de longitud l y masa despreciable. El péndulo está sometido a la fuerza gravitacional mg debida a su peso, y a la fuerza de fricción 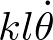$kl\dot \theta $, la cual se asume que es proporcional a la velocidad con un coeficiente de fricción k. La aplicación de la segunda ley de Newton (expresión (2.1)) permite escribir la ecuación del movimiento en la dirección tangencial:

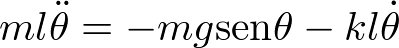$ml\ddot \theta = - mg{\rm{sen}}\theta - kl\dot \theta $ (2.20)

Como se sabe, siempre que sea posible hay que intentar elegir un eje coordenado que sea paralelo a la aceleración. En este caso, la escritura del movimiento en la dirección tangencial tiene la ventaja que la tensión en la cuerda, la cual es normal, no aparece en la ecuación. 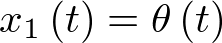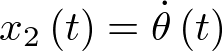Para obtener el modelo de estado del péndulo tomaremos como siempre las coordenadas posición y velocidad para el vector de estado, esto es, ${x_1}\left( t \right) = \theta \left( t \right)$ y ${x_2}\left( t \right) = \dot \theta \left( t \right)$. Entonces, el modelo de estado es:

\[\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right) = {x_2}\left( t \right)} \\ {{{\dot x}_2}\left( t \right) = - \frac{g}{l}{\rm{sen}}{x_1}\left( t \right) - \frac{k}{m}{x_2}\left( t \right)} \\ \end{array}\] (2.21)

Nótese el carácter no lineal del modelo de estado que, consecuentemente,  no admite escritura en forma matricial.

Figura 2.3. Circuito RLC con fuente de corriente.

Ejemplo 2.4. Circuito RLC.  Veamos ahora un sistema eléctrico. Sea pues el circuito  RLC de la Figura 2.3. Si en los modelos de estado de los sistemas mecánicos las variables de estado a con-siderar son la posición y velocidad, en los circuitos eléctricos interesa considerar la corriente y/o tensión en los elementos almacenadores de energía. Entonces, asumiendo que el condensador e inductor son elementos ideales, sus modelos de circuito están dados, respectivamente, por 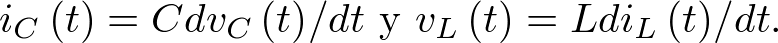${i_C}\left( t \right) = C{{d{v_C}\left( t \right)} \mathord{\left/ {\vphantom {{d{v_C}\left( t \right)} {dt\,\,}}} \right. \kern-\nulldelimiterspace} {dt\,\,}}{\rm{ y }}\,\,{v_L}\left( t \right) = L{{d{i_L}\left( t \right)} \mathord{\left/ {\vphantom {{d{i_L}\left( t \right)} {dt}}} \right. \kern-\nulldelimiterspace} {dt}}.$ Sea pues 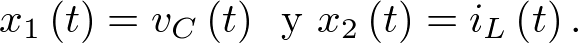${x_1}\left( t \right) = {v_C}\left( t \right)\,\,\,{\rm{ y}}\,\,{\rm{ }}{x_2}\left( t \right) = {i_L}\left( t \right).$ La entrada del sistema es la fuente de corriente  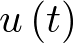y la salida la tensión en la carga 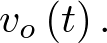${v_o}\left( t \right).$ Según lo anterior, el modelo de estado puede ser planteado del modo siguiente:

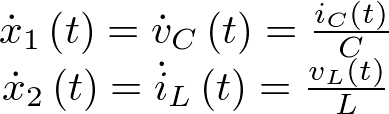$\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right) = {{\dot v}_C}\left( t \right) = \frac{{{i_C}\left( t \right)}}{C}} \\ {{{\dot x}_2}\left( t \right) = {{\dot i}_L}\left( t \right) = \frac{{{v_L}\left( t \right)}}{L}} \\ \end{array}$ (2.22)

Ahora, aplicando las leyes de Kirchhoff de corriente y tensión se establecen las relaciones que permiten escribir (2.22) en la forma 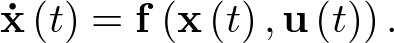${\bf{\dot x}}\left( t \right) = {\bf{f}}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right)} \right).$ Así, aplicando la ley de Kirchhoff de co-rriente en el nudo superior de la Figura 2.3 se tiene que:

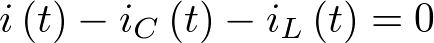$i\left( t \right) - {i_C}\left( t \right) - {i_L}\left( t \right) = 0$ (2.23)

Esto es,

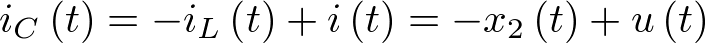${i_C}\left( t \right) = - {i_L}\left( t \right) + i\left( t \right) = - {x_2}\left( t \right) + u\left( t \right)$ (2.24)

La expresión anterior permite completar la primera ecuación de estado de (2.22). Respecto de la segunda, ésta se completa aplicando la ley de Kirchhoff de tensiones al lazo RLC. En él se cumple que

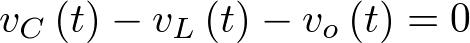${v_C}\left( t \right) - {v_L}\left( t \right) - {v_o}\left( t \right) = 0$ (2.25)

Esto es,

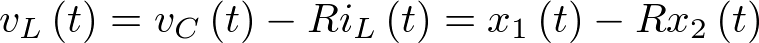${v_L}\left( t \right) = {v_C}\left( t \right) - R{i_L}\left( t \right) = {x_1}\left( t \right) - R{x_2}\left( t \right)$ (2.26)

Sustituyendo (2.24) y (2.26)  en la ecuación de estado (2.22) se tiene que

\[\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right) = - \frac{1}{C}{x_2}\left( t \right) + \frac{1}{C}u\left( t \right)} \\ {{{\dot x}_2}\left( t \right) = \frac{1}{L}{x_1}\left( t \right) - \frac{R}{L}{x_2}\left( t \right)} \\ \end{array}\] (2.27)

Respecto de la ecuación de salida está dada por

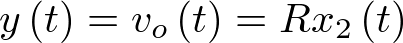$y\left( t \right) = {v_o}\left( t \right) = R{x_2}\left( t \right)$ (2.28)

El conjunto de ecuaciones (2.27) y (2.28)  permite escribir el modelo de estado del circuito del modo siguiente:

\[\left. {\begin{array}{*{20}{c}} {{\bf{\dot x}}\left( t \right) = {\bf{Ax}}\left( t \right) + {\bf{B}}u\left( t \right)} \\ {y\left( t \right) = {\bf{Cx}}\left( t \right)} \\ \end{array}} \right\} \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 & { - \frac{1}{C}} \\ {\frac{1}{L}} & { - \frac{R}{L}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {\frac{1}{C}} \\ 0 \\ \end{array}} \right)u\left( t \right)} \\ {y\left( t \right) = \left( {\begin{array}{*{20}{c}} 0 & R \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right)} \\ \end{array}} \right.\] (2.29)