Principal › Apuntes de Automática › CAPÍTULO 2 › 2.1 Modelado en el espacio de estado

2.1.1 Motivación

11 April, 2011 - 14:26 — joaquinm13
Versión para imprimirVersión para imprimir

Ejemplo 2.1. Sistema mecánico. Sea por ejemplo el sistema de la Figura 2.1 que representa un sistema muelle – masa – resorte, sujeto a sendos puntos fijos por ambos extremos. La variable 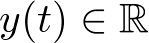$y\left( t \right) \in \mathbb{R}$ representa la posición de la masa m respecto de su posición de equilibrio 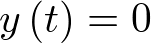$y\left( t \right) = 0$ . Aplicando la segunda ley de Newton al sistema:

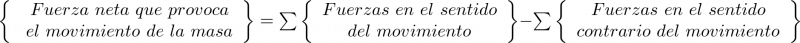$\left\{ {\,\,\begin{array}{*{20}{c}} {Fuerza\,\,neta\,\,que\,\,provoca} \\ {el\,\,movimiento\,\,de\,\,la\,\,masa} \\ \end{array} } \right\} = \sum {\left\{ {\begin{array}{*{20}{c}} {Fuerzas\,\,en\,\,el\,\,sentido} \\ {del\,\,movimiento} \\ \end{array} } \right\}} - \sum {\left\{ {\begin{array}{*{20}{c}} {Fuerzas\,\,en\,\,el\,\,sentido} \\ {contrario\,\,del\,\,movimiento} \\ \end{array} } \right\}} $ (2.1)

Esto es,

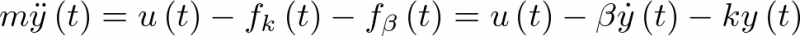$m\ddot y\left( t \right) = u\left( t \right) - {f_k}\left( t \right) - {f_\beta }\left( t \right) = u\left( t \right) - \beta \dot y\left( t \right) - ky\left( t \right)$ (2.2)

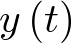Donde  \[\ddot y\left( t \right)\] representa, según la notación usual en mecánica, la derivada segunda de $y\left( t \right)$ respecto del tiempo (aceleración de la masa; 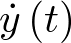$\dot y\left( t \right)$ sería la derivada primera, esto es, su velocidad); 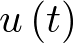$u\left( t \right)$ es la fuerza externa aplicada (entrada al sistema); \[{f_k}\left( t \right)\] es la fuerza de reacción del muelle, la cual, si se asume por simplificar que el muelle cumple la ley de Hooke, está dada por ${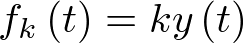f_k}\left( t \right) = ky\left( t \right)$. Por último, asumiendo también que el elemento de fricción (amortiguador) se comporta linealmente, su oposición al desplazamiento es proporcional a la velocidad del movimiento, \[{f_\beta }\left( t \right) = \beta \dot y\left( t \right)\].

Figura 2.1. Sistema muelle – masa – amortiguador.

El sistema de la Figura 2.1 se dice que es de segundo orden porque su dinámica depende de las dos primeras derivadas de 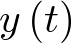. La ecuación diferencial (2.2) se denomina forzada o controlada porque el sistema está forzado o controlado por la entrada 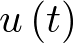. Si no hubiera influencia externa en el sistema (la ecuación estaría igualada a cero, ), éste  (su ecuación) se denominaría no forzado o autónomo. Desde la perspectiva acción – reacción, la entrada del sistema es la fuerza aplicada 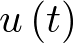y la salida el desplazamiento o respuesta 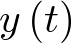. El sistema de la Figura 2.1 es lineal1  debido a las simplificaciones realizadas (ni el muelle ni el amortiguador lo son realmente) y, además invariante con el tiempo (la respuesta ante una misma excitación es la misma para todo tiempo t), aunque realmente no es así. Por ejemplo, el comportamiento del muelle dependerá de la temperatura de su entorno. Lo mismo sucederá con el comportamiento del fluido que contenga el amortiguador. No obstante lo anterior, la mayoría de los sistemas, dentro de ciertas condiciones de funcionamiento, pueden ser considerados lineales e invariantes con el tiempo o, de manera abreviada LTI (del inglés Linear Time-Invariant).
Cuando en 1683 Isaac Newton,  para muchos el científico más grande que ha dado la historia2, publicó los Philosophiae Naturalis Principia Mathematica3, el Cielo y la Tierra quedaron finalmente unificados en la Física, ya que demostró que las leyes naturales que gobiernan el movimiento en la Tierra y las que gobiernan el movimiento de los cuerpos celestes son las mismas4. Newton observó que el movimiento de los planetas podía ser predicho únicamente a partir de sus posiciones actuales y de sus velocidades. Esto es, no era necesario saber nada del movimiento pasado hasta el instante actual. Consecuentemente había definido el concepto de estado de un sistema dinámico (en este caso el sistema planetario) como el conjunto mínimo de variables (que denominaremos variables de estado) que permite determinar completamente su movimiento futuro. Este concepto será formalizado y generalizado en la sección siguiente.
El concepto de modelo de estado implica la representación del comportamiento dinámico de un sistema en base a un conjunto de ecuaciones diferenciales ordinarias (EDO) de primer orden, caracterizadas por la expresión siguiente:

\[\frac{{d{\bf{x}}\left( t \right)}}{{dt}} = {\bf{f}}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right)} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\] (2.3)

Esta ecuación vectorial se denomina ecuación de estado. En ella 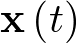${\bf{x}}\left( t \right)$ es el vector estado y sus coordenadas son las variables de estado (en el sistema mecánico de la Figura 2.1 sería un vector de 2 coordenadas: posición y velocidad). La variación del vector de estado respecto al tiempo se representa como una función vectorial, generalmente no lineal, cuyo argumento son los vectores de estado y de entrada5. El conjunto de todos los estados que puede alcanzar un sistema se denomina su espacio de estado. Puesto que cada estado estará caracterizado por un valor concreto de las variables de estado, el espacio de estado tiene por ejes coordenados las variables de estado. 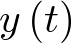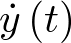Así por ejemplo, dado el sistema mecánico anterior, cuyo estado está determinado por su posición y velocidad, el espacio de estado para el sistema de la Figura 2.1 será de 2 dimensiones, con una coordenada que repre-senta la posición del sistema y otra la velocidad $\dot y\left( t \right)$.
El modelo de estado se completa con la ecuación de salida (2.4), la cual representa generalmente el conjunto de variables que pueden ser medidas y que constituyen la respuesta del sistema. La ecuación de salida es una función vectorial del vector de estado y del vector de entrada.

(2.4)

A modo de ejemplo, y por fijar ideas, vamos a escribir el modelo de estado del sistema de la Figura 2.1. En él, como se ha dicho más arriba, una coordenada del vector de estado 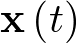${\bf{x}}\left( t \right)$ será la posición (sea pues  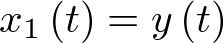${x_1}\left( t \right) = y\left( t \right)$) y la otra la velocidad (sea pues 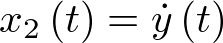${x_2}\left( t \right) = \dot y\left( t \right)$). Por supuesto el sistema es de orden 2, con lo cual la ecuación de estado en la forma (2.2) constará de dos ecuaciones diferenciales de primer orden, las cuales se obtienen a partir de sustituir las coordenadas del vector de estado en la ecuación (2.2). Esto es:

\[m{\dot x_2}\left( t \right) + \beta {x_2}\left( t \right) + k{x_1}\left( t \right) = u\left( t \right)\] (2.5)

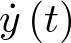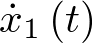Cabría preguntarse si se podría haberse sustituido $\dot y\left( t \right)$ por ${\dot x_1}\left( t \right)_{}^{}$, en vez de por 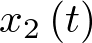${x_2}\left( t \right)$ como se ha hecho, sin embargo esta sustitución no cumpliría la ecuación (2.3) que exige una sola coordenada derivada por ecuación.
A partir de (2.5) basta con despejar la coordenada derivada del vector de estado (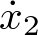${\dot x_2}$) y tener en cuenta que 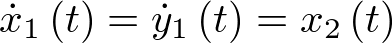${\dot x_1}\left( t \right) = {\dot y_1}\left( t \right) = {x_2}\left( t \right)$, de modo que la ecuación de estado del sistema de la Figura 2.1 en la forma 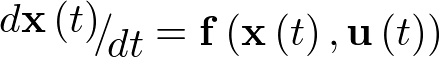${\raise0.7ex\hbox{${d{\bf{x}}\left( t \right)}$} \!\mathord{\left/ {\vphantom {{d{\bf{x}}\left( t \right)} {dt}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${dt}$}} = {\bf{f}}\left( {{\bf{x}}\left( t \right),{\bf{u}}\left( t \right)} \right)$ será:

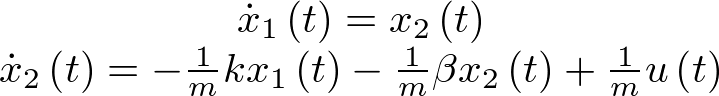$\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right) = {x_2}\left( t \right)} \\ {{{\dot x}_2}\left( t \right) = - \frac{1}{m}k{x_1}\left( t \right) - \frac{1}{m}\beta {x_2}\left( t \right) + \frac{1}{m}u\left( t \right)} \\ \end{array}$ (2.6)

Nótese que la entrada u(t) al sistema es un escalar en este caso. El modelo de estado se completa con la ecuación de salida en la forma (2.4), que en este caso estará dada por 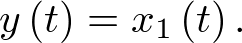$y\left( t \right) = {x_1}\left( t \right).$
Al ser el modelo de estado lineal6, éste, a partir de la ecuación (2.5) y la de salida, admite una representación matricial de la forma:

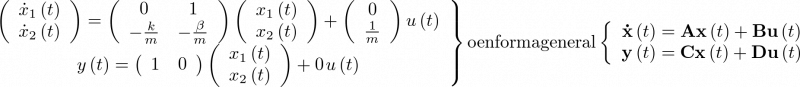$\left. \begin{array}{c} \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)} \\ {{{\dot x}_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 & 1 \\ { - \frac{k}{m}} & { - \frac{\beta }{m}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ {\frac{1}{m}} \\ \end{array}} \right)u\left( t \right) \\ y\left( t \right) = \left( {\begin{array}{*{20}{c}} 1 & 0 \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) + 0{\kern 1pt} u\left( t \right) \\ \end{array} \right\}{\rm{ o en forma general }}\left\{ {\begin{array}{*{20}{c}} {{\bf{\dot x}}\left( t \right) = {\bf{Ax}}\left( t \right) + {\bf{Bu}}\left( t \right)} \\ {{\bf{y}}\left( t \right) = {\bf{Cx}}\left( t \right) + {\bf{Du}}\left( t \right)} \\ \end{array}} \right.$ (2.7)

Donde A es una matriz de orden \[n \times n\], siendo n la dimensión del espacio de estado u orden del sistema (2 en el ejemplo). B es una matriz de orden \[n \times p\], siendo p el número de entradas del sistema, 1 en este caso. Respecto de la ecuación de salida, C es una matriz de orden \[q \times n\], siendo m las salidas del sistema (1 en el ejemplo). Por último, la matriz D (0 en este caso) es de orden \[q \times p\]. Normalmente los modelos de estado no tienen matriz D, lo cual indica que, como suele ser habitual, la entrada no influencia de modo directo a la salida.