Principal › Apuntes de Automática › CAPÍTULO 2 › 2.1 Modelado en el espacio de estado › 2.1.2 Formalización

Revisión de 2.1.2 Formalización de 24 May, 2011 - 12:16

24 May, 2011 - 00:29 — joaquinm13
Versión para imprimirVersión para imprimir

A continuación se van a formalizar los conceptos introducidos en la sección anterior. Esto se hará para el dominio de tiempo continuo (ecuaciones diferenciales); para el dominio de tiempo discreto (ecuaciones en diferencias) se realizará en la sección 2.5.

Tiempo continuo

El estado de un sistema es una colección de variables, denominadas variables de estado, que reúnen la información suficiente sobre el pasado del mismo, de tal manera que su conocimiento en el instante actual 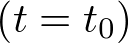$\left( {t = {t_0}} \right)$ junto con el de la entrada para el momento presente y futuro 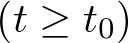$\left( {t \ge {t_0}} \right)$, permite determinar el comportamiento del sistema para cualquier $t \ge {t_0}$.
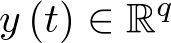Las variables de estado componen un vector \[{\mathbf{x}}\left( t \right) \in {\mathbb{R}^n}\] denominado vector de estado. Las variables de control (o de entrada) forman el vector de entrada \[{\mathbf{u}}\left( t \right) \in {\mathbb{R}^p}\], y las señales medidas (respuestas) constituyen el vector de salida $y\left( t \right) \in {\mathbb{R}^q}$. A partir de aquí, un sistema dinámico invariante con el tiempo7 puede ser representado por las ecuaciones: