Principal › Apuntes de Automática › CAPÍTULO 2 › 2.5 Sistemas en tiempo discreto › 2.5.1 Motivación

Revisión de 2.5.1 Motivación de 14 June, 2011 - 14:48

13 June, 2011 - 20:41 — joaquinm13
Versión para imprimirVersión para imprimir
Figura 2.14. Definición de derivada.

Ejemplo 2.10. Solución aproximada de una ecuación diferencial ordinaria. Considérese el cálculo numérico de una ecuación diferencial ordinaria de primer orden y sea ésta, como ejemplo, la siguiente:

  (2.91)

La rama de las matemáticas que soluciona este tipo de problemas es el análisis o cálculo numérico. Esta disciplina crea algoritmos que permiten resolver problemas, en los que estén involucradas cantidades numéricas, con una precisión determinada.
El análisis numérico es de aplicación cuando: 1) Los problemas no tienen solución analítica o 2) el coste de cálculo de la solución analítica es mayor que la numérica. Para la resolución de ecuaciones diferenciales ordinarias los métodos más utilizados son el método de Euler y los métodos de Runge-Kutta22.
Volviendo con el ejemplo, nótese en la Figura 2.14 que para T pequeño,  puede aproximarse por la relación incremental (definición de derivada) siguiente:

  (2.92)

Resolviendo la ecuación anterior para 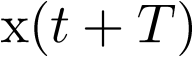$x\left( {t + T} \right)$ se tiene que

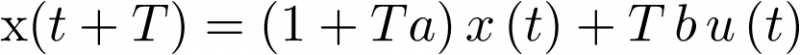$x\left( {t + T} \right) = \left( {1 + Ta} \right)x\left( t \right) + T\,b\,u\left( t \right)$ (2.93)

Evaluando esta ecuación para un tiempo discreto cualquiera t = kT se obtiene la ecuación en diferencias siguiente:

$x\left[ {\left( {k + 1} \right)T} \right] = \left( {1 + Ta} \right)x\left( {kT} \right) + T\,b\,u\left( {kT} \right)$ (2.94)

La cual, para un T dado, puede ser escrita como

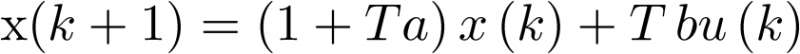$x\left( {k + 1} \right) = \left( {1 + Ta} \right)x\left( k \right) + T\,bu\left( k \right)$ (2.95)

La expresión anterior indica que el valor de la trayectoria (solución) en el instante de tiempo 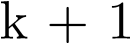$k + 1$ se calcula a partir del valor de x y de la excitación (entrada) u en el instante k.

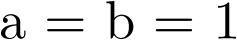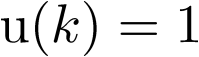La ecuación diferencial original (2.91) ha sido pues transformada por este método numérico sencillo (denominado de Euler23) en la ecuación en diferencias (2.94). Ésta puede ser programada ahora mediante un algoritmo numérico simple en un computador. Así por ejemplo, si $a{\rm{ = }}b{\rm{ = 1}}$,  y $u\left( k \right) = 1$ para k par;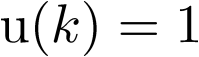${\rm{ }}u\left( k \right) = 0$ para k impar, y 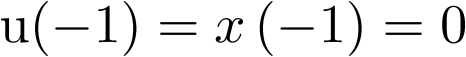$u\left( { - 1} \right) = x\left( { - 1} \right) = 0$, se tiene que las primeras 5 muestras de 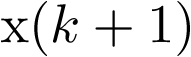$x\left( {k + 1} \right)$ valen