Principal › Apuntes de Automática › CAPÍTULO 2 › 2.5 Sistemas en tiempo discreto › 2.5.2 Formalización

Revisión de 2.5.2 Formalización de 14 June, 2011 - 21:47

14 June, 2011 - 21:47 — joaquinm13
Versión para imprimirVersión para imprimir

En los sistemas discretos 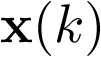${\bf{x}}\left( k \right)$ es una secuencia vectorial cuyo valor en cualquier punto de la secuencia es el estado del sistema en ese instante de tiempo discreto. También, al igual que en los sistemas continuos, el espacio de estado se define como el espacio vectorial donde toma valores el vector de estado 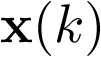${\bf{x}}\left( k \right)$. De la misma forma, teniendo en cuenta que el estado se concreta como la mínima cantidad de información (mínimo conjunto de variables) precisa para conocer la evolución del sistema para todo kT, las variables de estado en tiempo discreto son también linealmente independientes, con lo cual la dimensión del espacio de estado coincide con el número de variables de estado.
En virtud de lo anterior y por analogía con los sistemas continuos, se define como modelo de estado discreto de un sistema dinámico invariante con el tiempo, para un periodo de muestreo T dado, una relación matemática entre dos secuencias de entrada 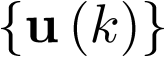$\left\{ {{\bf{u}}\left( k \right)} \right\}$ y salida 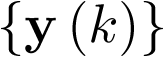$\left\{ {{\bf{y}}\left( k \right)} \right\}$ del modo siguiente: