Principal › Apuntes de Automática › CAPÍTULO 2 › 2.1 Modelado en el espacio de estado › 2.1.1 Motivación

Revisión de 2.1.1 Motivación de 20 May, 2011 - 01:35

11 April, 2011 - 14:26 — joaquinm13
Versión para imprimirVersión para imprimir

Ejemplo 2.1. Sistema mecánico. Sea por ejemplo el sistema de la Figura 2.1 que representa un sistema muelle – masa – resorte, sujeto a sendos puntos fijos por ambos extremos. La variable 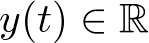$y\left( t \right) \in \mathbb{R}$ representa la posición de la masa m respecto de su posición de equilibrio 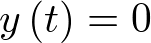$y\left( t \right) = 0$ . Aplicando la segunda ley de Newton al sistema:

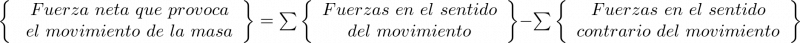$\left\{ {\,\,\begin{array}{*{20}{c}} {Fuerza\,\,neta\,\,que\,\,provoca} \\ {el\,\,movimiento\,\,de\,\,la\,\,masa} \\ \end{array} } \right\} = \sum {\left\{ {\begin{array}{*{20}{c}} {Fuerzas\,\,en\,\,el\,\,sentido} \\ {del\,\,movimiento} \\ \end{array} } \right\}} - \sum {\left\{ {\begin{array}{*{20}{c}} {Fuerzas\,\,en\,\,el\,\,sentido} \\ {contrario\,\,del\,\,movimiento} \\ \end{array} } \right\}} $ (2.1)

Esto es,

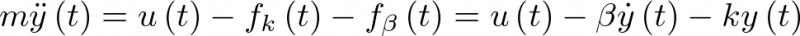$m\ddot y\left( t \right) = u\left( t \right) - {f_k}\left( t \right) - {f_\beta }\left( t \right) = u\left( t \right) - \beta \dot y\left( t \right) - ky\left( t \right)$ (2.2)

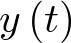Donde  \[\ddot y\left( t \right)\] representa, según la notación usual en mecánica, la derivada segunda de $y\left( t \right)$ respecto del tiempo (aceleración de la masa; 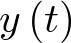$\dot y\left( t \right)$ sería la derivada primera, esto es, su velocidad); 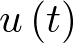$u\left( t \right)$ es la fuerza externa aplicada (entrada al sistema); \[{f_k}\left( t \right)\] es la fuerza de reacción del muelle, la cual, si se asume por simplificar que el muelle cumple la ley de Hooke, está dada por ${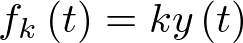f_k}\left( t \right) = ky\left( t \right)$. Por último, asumiendo también que el elemento de fricción (amortiguador) se comporta linealmente, su oposición al desplazamiento es proporcional a la velocidad del movimiento, \[{f_\beta }\left( t \right) = \beta \dot y\left( t \right)\].

Figura 2.1. Sistema muelle – masa – amortiguador.

El sistema de la Figura 2.1 se dice que es de segundo orden porque su dinámica depende de las dos primeras derivadas de 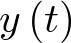. La ecuación diferencial (2.2) se denomina forzada o controlada porque el sistema está forzado o controlado por la entrada 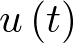. Si no hubiera influencia externa en el sistema (la ecuación estaría igualada a cero, ), éste  (su ecuación) se denominaría no forzado o autónomo. Desde la perspectiva acción – reacción, la entrada del sistema es la fuerza aplicada 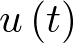y la salida el desplazamiento o respuesta 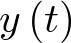. El sistema de la Figura 2.1 es lineal1  debido a las simplificaciones realizadas (ni el muelle ni el amortiguador lo son realmente) y, además invariante con el tiempo (la respuesta ante una misma excitación es la misma para todo tiempo t), aunque realmente no es así. Por ejemplo, el comportamiento del muelle dependerá de la temperatura de su entorno. Lo mismo sucederá con el comportamiento del fluido que contenga el amortiguador. No obstante lo anterior, la mayoría de los sistemas, dentro de ciertas condiciones de funcionamiento, pueden ser considerados lineales e invariantes con el tiempo o, de manera abreviada LTI (del inglés Linear Time-Invariant).
Cuando en 1683 Isaac Newton,  para muchos el científico más grande que ha dado la historia2, publicó los Philosophiae Naturalis Principia Mathematica3, el Cielo y la Tierra quedaron finalmente unificados en la Física, ya que demostró que las leyes naturales que gobiernan el movimiento en la Tierra y las que gobiernan el movimiento de los cuerpos celestes son las mismas4. Newton observó que el movimiento de los planetas podía ser predicho únicamente a partir de sus posiciones actuales y de sus velocidades. Esto es, no era necesario saber nada del movimiento pasado hasta el instante actual. Consecuentemente había definido el concepto de estado de un sistema dinámico (en este caso el sistema planetario) como el conjunto mínimo de variables (que denominaremos variables de estado) que permite determinar completamente su movimiento futuro. Este concepto será formalizado y generalizado en la sección siguiente.
El concepto de modelo de estado implica la representación del comportamiento dinámico de un sistema en base a un conjunto de ecuaciones diferenciales ordinarias (EDO) de primer orden, caracterizadas por la expresión siguiente: