A. Javier Barragán Piña

Versión para imprimir

En la figura se puede observar el esquema simplificado de una planta hidroeléctrica. La electricidad es generada mediante la turbina al ser movida por el agua a presión que se evacua por el canal de desagüe de un embalse.

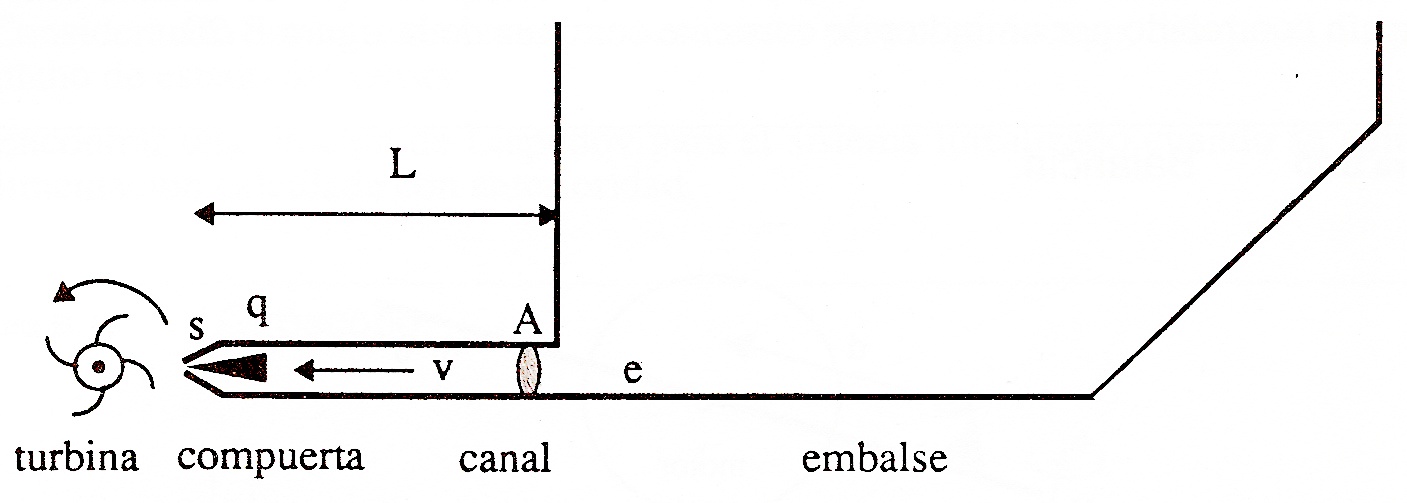
La potencia generada por la central es función de la velocidad con la circula el agua por el canal de acceso a la turbina, $v(t)$. Dicha velocidad viene determinada por la ecuación (1), donde $K_1$ y $K_2$ son constantes, $g$ es la aceleración de la gravedad, $L$ es la longitud del canal de desagüe, $e$ la presión a la entrada del canal, la cual se supone constante y $q(t)$ es la apertura de la compuerta del canal.

$$\dfrac{\text{d}v(t)}{\text{d}t} = \dfrac{K_2 \text{g}}{\text{L}}\left( e - K_1\dfrac{v(t)^2}{q(t)^2}\right) \quad\quad (1)$$

Nota: La ecuación (1) sólo tiene sentido para valores estrictamente positivos de $v(t)$ y $q(t)$.

Debido al tamaño de la compuerta, ésta tarda un tiempo en moverse desde que se le da la orden. Siendo $u(t)$  la señal de control del sistema (la orden para la compuerta), la dinámica de la apertura de la misma viene dada por la ecuación diferencial:

$$\dfrac{\text{d}q(t)}{\text{d}t} = 2 \left(u(t) - q(t)\right) \quad\quad (2)$$

Se solicita:

1. Utilice las ecuaciones (1) y (2) para escribir un modelo de estado del sistema.
2. Determine el estado de equilibrio del sistema siendo $u_{eq} = 0.5$.
3. Linealice el sistema en el estado de equilibrio obtenido. Recuerde que:$$\dot{\mathbf{x}} \simeq \mathbf{A} (\mathbf{x} - \mathbf{x}_{eq}) + \mathbf{B} (\mathbf{u} - \mathbf{u}_{eq})$$

   $${\small \mathbf{A} = \left.\left(\begin{array}{cccc} \dfrac{\partial f_1}{\partial x_1} & \dfrac{\partial f_1}{\partial x_2} & \cdots & \dfrac{\partial f_1}{\partial x_n}\\ \dfrac{\partial f_2}{\partial x_1} & \dfrac{\partial f_2}{\partial x_2} & \cdots & \dfrac{\partial f_2}{\partial x_n}\\ \cdots & \cdots & \ddots & \cdots\\ \dfrac{\partial f_n}{\partial x_1} & \dfrac{\partial f_n}{\partial x_2} & \cdots & \dfrac{\partial f_n}{\partial x_n}\\ \end{array}\right)\right|_{ \begin{array}{l} \mathbf{x}=\mathbf{x}_{eq}\\ \mathbf{u}=\mathbf{u}_{eq} \end{array} } }$$

   $${\small \mathbf{B} = \left.\left(\begin{array}{cccc} \dfrac{\partial f_1}{\partial u_1} & \dfrac{\partial f_1}{\partial u_2} & \cdots & \dfrac{\partial f_1}{\partial u_m}\\ \dfrac{\partial f_2}{\partial u_1} & \dfrac{\partial f_2}{\partial u_2} & \cdots & \dfrac{\partial f_2}{\partial u_m}\\ \cdots & \cdots & \ddots & \cdots\\ \dfrac{\partial f_n}{\partial u_1} & \dfrac{\partial f_n}{\partial u_2} & \cdots & \dfrac{\partial f_n}{\partial u_m}\\ \end{array}\right)\right|_{ \begin{array}{l} \mathbf{x}=\mathbf{x}_{eq}\\ \mathbf{u}=\mathbf{u}_{eq} \end{array} } }$$

4. Obtenga en una misma figura el retrato de fase del sistema no lineal y del sistema linealizado para $u(t) = u_{eq} = 0.5$. Considere para ello que $L=7m$, $K_1=2000 Kg/m^3$, $K_2=0.00001m^2s^2/Kg$, $e=200.000Pa$ y $g = 9.8 m/s^2$.
5. En vista de la simulación anterior, ¿cuál considera usted que es la zona válida para la linealización realizada? Argumente su respuesta.
6. Explique la relación entre los retratos de fase obtenidos y los autovalores de la matriz de estado del sistema linealizado.