A. Javier Barragán Piña

Versión para imprimir

Se desea diseñar el sistema de control de la figura. Teniendo en cuenta las características propias de la aplicación, se ha optado por diseñar un sistema de control exento de error de posición y con un error de velocidad menor del 10%. El tiempo de asentamiento deberá ser inferior a 1 segundo, y el sobreimpulso máximo admitido es del 5%.

 

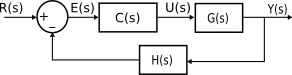$C(s)=K_1$, $G(s)=\dfrac{1}{(s^2+3s)}$ y $H(s)=K_2s+1$

 

1. Obtener las relaciones que deben satisfacer K1 y K2 para que se cumplan los requerimientos del diseño.
2. Dibujar sobre el plano S la región donde deben ser ubicados los polos de lazo cerrado para que se cumplan las especificaciones temporales.
3. Escoger un valor adecuado para K1 y K2.
4. Calcular analíticamente el error estático de posición y de velocidad que cometerá el sistema.
5. Simule el comportamiento del sistema frente a una entrada de tipo escalón y frente a una entrada de tipo rampa, comprobando el cumplimiento de los requisitos del diseño.
6. Compruebe mediante simulación si se cumplen los cálculos del apartado 4).

 

Resolución:

 

Los requerimientos del diseño son:

 

Error de posición --> e_ss (pos) = 0 (exento de error de posición ).
Error de velocidad --> e_ss (vel) < 10%
Tiempo de establecimiento --> t_s (2%) < 1 seg
Sobreimpulso --> Mp< 5%

 

En primer lugar vemos de que tipo es el sistema calculando su FT de lazo abierto, que es:

 

$ FT = C(s) G(s) H(s) = K_1  \dfrac{1}{{(s^2 + 3s)}} (K_2 s + 1) = \dfrac{{K_1 K_2 s + K_1 }}{{s(s + 3)}}$ Vemos que es de tipo 1, por lo que el e_ss (pos) será cero, por lo que no hace falta calcularlo.

 

Para calcular el e_ss(vel) lo haremos de dos modos: uno usando la expresión del error de realimentación, y otro usando el error real.

 

Modo 1--> El error de realimentación a partir del diagrama de bloques es:

 

$ \left. \begin{array}{l}
\mu (s) = Y(s) H(s) \\
E(s) = R(s) - \mu (s) \\
Y(s) = E(s) C(s) G(s) \\
\end{array} \right\}E(s) = R(s) - E(s) C(s) G(s) H(s){\rm{ }} \Rightarrow $

 

$ \Rightarrow {\rm{ }}E(s) = R(s)\dfrac{1}{{1 + C(s) G(s) H(s)}} = R(s)\dfrac{{s(s + 3)}}{{s(s + 3) + K_1 (1 + K_2 s)}}$

 

Ahora aplicamos el teorema del valor final con una señal de entrada rampa R(s)=1/s²:

 

$ e_{ss} (vel) = \lim \limits _{x \to 0} s E(s) = \lim \limits_{x \to 0} s R(s)\dfrac{s(s + 3)}{s(s + 3) + K_1 (1 + K_2 s)} = $

 

$ = \lim \limits_{x \to 0} s \dfrac{1}{s^2} \dfrac{s(s + 3)}{s(s + 3) + K_1 (1 + K_2 s)} = \dfrac{3}{K_1 (1 + 0)} = \dfrac{3}{K_1 }$

 

Sabemos que uno de los requisitos que tiene que cumplir es que e_ss (vel)< 10%, por tanto:

 

$ \dfrac{3}{{K_1 }} < 0,1{\rm{ }} \Rightarrow {\rm{ }}K_1 > \dfrac{3}{{0,1}}{\rm{ }} \Rightarrow {\rm{ }}K_1 > 30$

 

Calculamos la FT de lazo cerrado:

 

$ FTLC = \dfrac{Y(s)}{R(s)} = \dfrac{C(s) G(s)}{1 + C(s) G(s) H(s)} = \dfrac{K_1 \dfrac{1}{(s^2 + 3s)}}{1 + K_1 \dfrac{1}{(s^2 + 3s)}(K_2 s + 1)} = $

 

$ = \dfrac{K_1 }{s(s + 3) + K_1(1 + K_2 s)} = \dfrac{K_1 }{s^2 + (3 + K_1K_2 )s + K_1}$

AVISO: La comparación del sistema resultante con un sistema de orden 2 es sólo válida cuando puede realizarse, es decir, cuando el sistema resultante también es de orden 2 o tiene 2 polos dominantes. Sin embargo, en la mayoría de los casos esto no es así. Para esos casos donde la comparación no es posible, es necesario trazar el Lugar Geométrico de la Raíces del sistemas y así, mediante su análisis, saber cómo se comportará en función del parámetro a diseñar.

Comprobamos que el sistema es de 2º orden, por lo que el sobreimpulso será:

 

$ Mp = e^{\dfrac{ - \delta \pi }{\sqrt {1 - \delta ^2 }}}$

 

De esta expresión despejaremos el coeficiente de amortiguamiento $\delta$, quedando:

$ \delta = \sqrt {\dfrac{\ln ^2 Mp}{\pi + \ln ^2 Mp}} = \sqrt {\dfrac{\ln ^2 0,05}{\pi + \ln ^2 0,05}} = 0,69$

 

Como Mp debe ser menor del 5%, observamos como cambian los polos al variar $\delta$ en los dos casos, que son:

 

$ p_{1,2} = - \delta \omega _n \pm j\omega _n \sqrt {1 - \delta ^2 } \left\{ \begin{array}{l}
\delta \text{tiende a 0} \Rightarrow p_{1,2} = \pm j\omega _n \sqrt {1 - \delta ^2 } \Rightarrow \text{Oscila y aumenta Mp} \\
\delta \text{tiende a 1} \Rightarrow p_{1,2} = - \omega _n \Rightarrow \text{Mp tiende a 0} \\
\end{array} \right.$

 

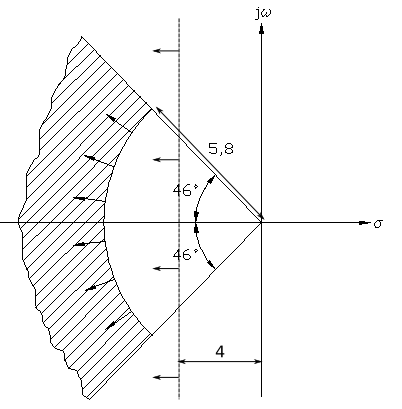
Por tanto, $\mathbf{\delta > 0.69}$.

 

El tiempo de establecimiento en los sistemas de 2º orden para un rango del 2% es:

 

$ t_s (2\% ) = \dfrac{4}{{\delta \omega _n }} < 1{\rm{ seg}}$

 

De donde podemos despejar la frecuencia natural no amortiguada ω_n:

 

$ \omega _n > \dfrac{4}{{\delta t_s }} = \dfrac{4}{{0,69 · 1}} = 5,8{\rm{ }}rad/s$

 

Puesto que:

 

$ \cos \beta = \delta = 0,69{\rm{ }} \Rightarrow {\rm{ }}\beta {\rm{ = arcos 0}}{\rm{,69 = 46}}{\rm{,37}}^ \circ$

 

Como δ>0,69 esta aumenta , lo que hace que p_1,2 tiendan a ser más reales, y por tanto β menor. Así que β < 46,37º.

 

Obtenemos la parte real de los polos a partir de la expresión de t_s:

 

$ \dfrac{4}{{\delta \omega _n }} < 1{\rm{ }} \Rightarrow {\rm{ }}\delta \omega _n > 4{\rm{ }} \Rightarrow {\rm{ - }}\delta \omega _n < - 4$

 

Los polos de lazo cerrado en el plano S se dibujarán como:

 

 

Por último, obtendremos la expresión para K2 comparando la FTLC con la expresión modelo de un sistema de 2º orden, debiéndose cumplir las inecuaciones anteriores.

 

$ \dfrac{{K_1 }}{{s^2 + (3 + K{}_1K_2 )s + K_1 }} = \dfrac{{K_0 \omega _n^2 }}{{s^2 + 2\delta \omega _n s + \omega _n^2 }}$

 

La frecuencia natural no amortiguada será:

 

$ \omega _n^2 = K_1 {\rm{ }}{\rm{, }}\omega _n^{} = \sqrt {K_1 } \Rightarrow {\rm{ }}\omega _n^{} > \sqrt {30} = 5,48{\rm{ }}rad/s$

 

Al ser este valor menor que antes es menos restrictivo, por lo que nos quedamos con el anterior para el diseño, siendo el requisito:

 

$ K_1 {\rm{ = }}\omega _n^2 {\rm{ }} = 5,8^2 {\rm{ = 33}}{\rm{,64 }} \Rightarrow {\rm{ }}K_1 > 33,64$

 

Y la expresión para el coef. de amortiguamiento $\delta$ será:

 

$ \delta = \dfrac{{3 + K_1 K_2 }}{{2\omega _n }}$

 

A continuación escogeremos valores para K1 y K2. Para ello tendremos en cuenta que se cumplan los requisitos calculados K1>33,64 y δ>0,69.

 

Obtenemos un valor de K2 sustituyendo estos valores en la última expresión que hemos obtenido y despejando:

 

$ K_2 = \dfrac{{2\delta \sqrt {K_1 } - 3}}{{K_1 }} = \dfrac{{2 · 0,69\sqrt {33,64} - 3}}{{33,64}} = 0,148{\rm{ }} \Rightarrow {\rm{ }}K_2 > 0,148$

 

Con esto, y dando un valor a K1 y a K2 que no estén muy lejos de los límites calculados pero tampoco demasiado cerca (p.ej. K1=35 y K2=0,18) obtenemos δ, que será:

 

$ \delta = \dfrac{{3 + K_1 K_2 }}{{2\omega _n }} = \dfrac{{3 + 35 · 0,18}}{{2\sqrt {35} }} = 0,78$

 

Comprobamos que cumple el requisito de diseño.

 

Y el sobreimpulso será:

 

$ Mp = e^{\dfrac{{ - \delta \pi }}{{\sqrt {1 - \delta ^2 } }}} = e^{\dfrac{{ - 0,78\pi }}{{\sqrt {1 - 0,78^2 } }}} = 0,02{\rm{ }}(2\% )$

 

Modo 2--> Calculando el Error Real del sistema:

 

Nota: Este apartado no era necesario calcularlo en el examen.

 

$ \left. \begin{array}{l}
E'(s) = R(s) - Y(s) \\
FTLC = \dfrac{{Y(s)}}{{R(s)}} = \dfrac{{K_1 }}{{s^2 + (3 + K{}_1K_2 )s + K_1 }} \\
\end{array} \right\}E'(s) = R(s){\rm{ }}\left( {{\rm{1 - }}\dfrac{{K_1 }}{{s^2 + (3 + K{}_1K_2 )s + K_1 }}} \right) \Rightarrow $

 

$ \Rightarrow {\rm{ }}E'(s) = R(s)\left( {\dfrac{{s(s + 3 + K_1 K_2 )}}{{s^2 + s(3 + K_1 K_2 ) + K_1 }}} \right)$

 

Ahora aplicamos el teorema del valor final con una señal de entrada rampa R(s)=1/s²:

 

$e_{ss} (vel) = \lim \limits_{x \to 0} s E'(s) = \lim \limits_{x \to 0} s R(s)\dfrac{s(s + 3 + K_1 K_2 )}{s^2 + s(3 + K_1 K_2 ) + K_1 } = $

 

$ = \lim \limits_{x \to 0} s \dfrac{1}{s^2 } \dfrac{s(s + 3 + K_1 K_2 )}{s^2 + s(3 + K_1 K_2 ) + K_1 } = \dfrac{3 + K_1 K_2 }{K_1} = \dfrac{3}{K_1 } + K_2$

 

Sabemos que uno de los requisitos que tiene que cumplir es que e_ss (vel)< 10%, por tanto:

$ \dfrac{3}{{K_1 }} + K_2 < 0,1{\rm{ }} \Rightarrow {\rm{ }}K_1 > \dfrac{3}{{0,1 - K_2 }}{\rm{ }}{\rm{, }}K_2 < \dfrac{{0,1K_1 - 3}}{{K_1 }}$

 

Al igual que antes, en principio los requisitos serán δ>0,69 (por tanto β<46,37º).

 

A continuación escogeremos valores para K1 y K2. Para ello tendremos en cuenta que se cumplan los requisitos calculados $ K_1 > \dfrac{3}{{0,1 - K_2 }}{\rm{ }}{\rm{, }}K_2 < \dfrac{{0,1K_1 - 3}}{{K_1 }}{\rm{ }}y{\rm{ }}\delta > 0,69$.

 

Obtenemos un valor de K2 dando un valor a K1 adecuado (p.ej., el de antes K1=35) y sustituyendo estos valores en las expresiones que hemos obtenido antes:

 

$ K_2 < \dfrac{{0,1K_1 - 3}}{{K_1 }} = \dfrac{{0,1 · 35 - 3}}{{35}} = 0,0142{\rm{ }} \Rightarrow {\rm{ }}K_2 < 0,0142$

 

$ K_2 < \dfrac{{2\delta \sqrt {K_1 } - 3}}{{K_1 }} = \dfrac{{2 · 0,69\sqrt {35} - 3}}{{35}} = 0,147{\rm{ }} \Rightarrow {\rm{ }}K_2 < 0,147$
El primero es más restrictivo, por lo que damos un valor a K2 que no esté muy lejos de este límite pero tampoco demasiado cerca (p.ej. K2=0,01).

 

Comprobamos los resultados obtenidos en los dos modos de hacer el ejercicio mediante simulación en Matlab.

 

El código que genera todas las simulaciones es:

clc, clear all, close all
K1=35;
K2=0.18;
G=tf(1,[1,3,0]);
H=tf([K2,1],1);
S=feedback(K1*G,H); %FT= Y(s)/R(s)

%Simulacion frente a entrada ESCALON (Solo para comprobar que es casi cero)
t=0:1e-3:3;

figure
[y,t]=step(S,t);
u=ones(size(t)); %Escalon
ess_pos=u(end)-y(end) %error de posicion
plot(t,y,t,u,'r--'), xlabel('Tiempo (s)'), ylabel('Escalon')

%Simulacion frente a entrada RAMPA (unitaria)
r=t; %Funcion rampa unitaria

%Modo 1: Error de realimetacion
E_REALIM=tf([1,3,0],[1,3+K1*K2,K1]);
[e_vel,t]=lsim(E_REALIM,r,t);
figure,plot(t,e_vel), xlabel('Tiempo (s)'), ylabel('Error de realimentacion')
ess_vel_realim=e_vel(end) %error de velocidad de realimentacion
ess_vel_realim_teorico=3/K1 %error de velocidad de realimentacion teorico

%Modo 1: Error real
K1=35;
K2=0.01;
G=tf(1,[1,3,0]);
H=tf([K2,1],1);
S=feedback(K1*G,H); %FT= Y(s)/R(s)

r=t; %Funcion rampa unitaria
[y2,t]=lsim(S,r,t);
ess_vel_real=r(end)-y2(end) %error de velocidad real
ess_vel_real_teorico=(3/K1)+K2 %error de velocidad real teorico
figure,plot(t,y2,t,r,'r--'), xlabel('Tiempo (s)'), ylabel('Rampa')

 

 

 

 

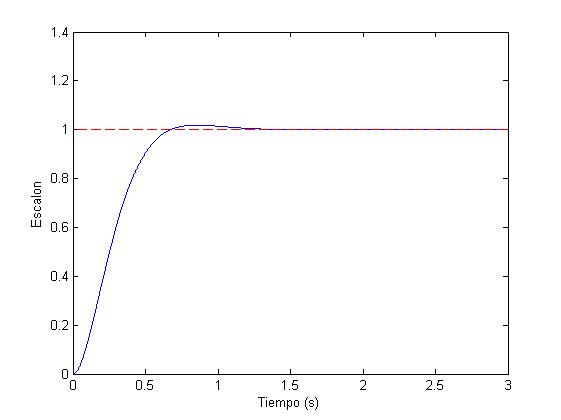
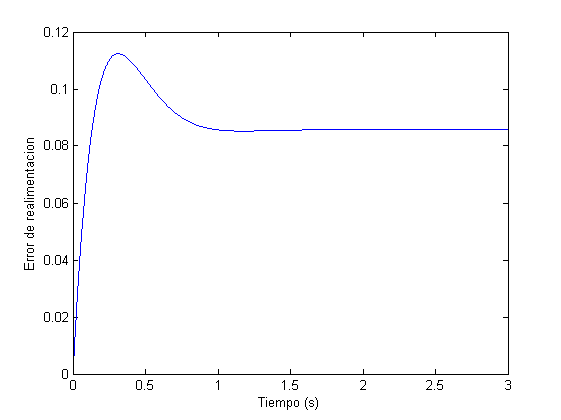
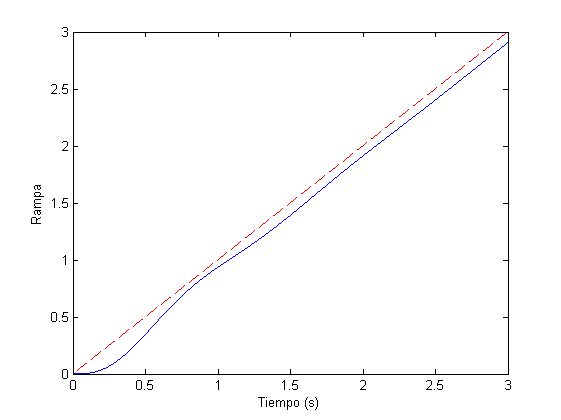
Como puede observarse, tanto en los resultados de la consola como en las representaciones gráficas, se cumplen las condiciones del diseño. Las pequeñas diferencias existentes entre los errores teóricos y reales (según la simulación) son producidos porque el tiempo de simulación evidentemente no es infinito. Conforme se aumenta el tiempo de simulación, los errores teóricos y reales (según la simulación) tienden a converger al mismo valor.