Inicie su sesión para modificar los apuntes, usar los foros, etc. Si no es usuario de la web, regístrese.
Resuelto. 2007, junio. Ejercicio práctico (4 puntos)
En la figura se muestra el vehículo explorador de Marte Spirit, el cual se puede controlar desde la Tierra mediante órdenes de trayectorias. Considerando que el diagrama de bloques simplificado del sistema es el que se muestra en la figura, se desea diseñar el sistema de control de velocidad del vehículo de forma que responda adecuadamente a los siguientes criterios de diseño:
- Cuando se ordene al vehículo mantener una velocidad constante (entrada escalón), deberá seguirla con un error menor del 0.1%; mientras que si la referencia enviada desde la Tierra es una aceleración constante (entrada rampa), bastará con que el Spirit la siga con un error inferior al 50%.
- Otra característica muy importante en el control del vehículo es que debe comportarse correctamente frente a las abundantes perturbaciones del terreno (rocas, cambios de pendiente, etc.), por lo que se ha de conseguir que el efecto de las perturbaciones sobre la salida del sistema sea inferior al 10% (considerando una perturbación constante de valor 1, escalón unitario).
- Por motivos de diseño, la ganancia del sensor empleado, K1, ha de estar comprendida entre 1 y 3.


$G\left ( s \right )=\dfrac{1}{s(s+1)(s+3)}$ $H\left ( s \right )=K_1s$
$C_1\left ( s \right ) = \dfrac {K_2}{s}$
$C_2\left ( s \right ) = K_2$
- Escoja uno de los siguientes controladores para poder cumplir los requerimientos del diseño.
- Determine las relaciones que deben cumplir K1 y K2 para mantener al sistema en la zona de estabilidad asintótica (test de Routh).
- Determine las relaciones que deben cumplir K1 y K2 para satisfacer las exigencias del diseño.
- Escoja un valor apropiado para K1 y K2 teniendo en cuenta los resultados anteriores y la limitación dada en el enunciado para K1.
- Simule el sistema para una entrada de referencia de tipo escalón y de tipo rampa unitarias, y compruebe si se cumplen los requisitos de diseño. Comente los resultados de la simulación.
- Simule el sistema con una perturbación dada por un escalón unitario, manteniendo la entrada de referencia a 0, y compruebe si se cumplen los requerimientos del diseño.
Recuerde: $x(\infty) = \lim_{s \to 0}sX\left ( s \right )$
Resolución:
a) En primer lugar debemos simplificar la realimentación interna formada por las funciones de transferencia G(s) y H(s). Si llamamos a la función de transferencia resultante G2(s), tenemos el siguiente diagrama de bloques reducido:
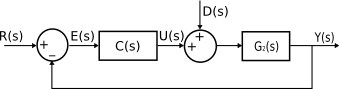
con $G_2\left ( s \right )=\dfrac {G\left ( s \right )}{1+G\left ( s \right )H\left ( s \right )} = \dfrac {\dfrac {1}{s(s+1)(s+3)}}{1+\dfrac {1}{s(s+1)(s+3)} K_1s} = \dfrac {1}{s(s+1)(s+3)+K_1s} = \dfrac {1}{s(s^2+4s+3+K_1)}$
Como puede observarse, G2(s) posee un polo en s=0, es decir, si C(s) no modifica el número de tipo del sistema, será de tipo 1. Para cumplir las especificaciones de error del ejercicio nos basta con que el sistema sea de tipo 1, ya que de esta forma tendrá error nulo para una entrada escalón y constante para una entrada de tipo rampa.
Como G2(s) ya tiene el número de tipo necesario, escogeremos el controlador dado por C2(s)=K2. Si se amenta el número de tipo de forma innecesaria se complica la estabilización del sistema. Es este caso concreto, si se escogiese C1(s) se puede comprobar fácilmente mediante el criterio de Routh que resulta imposible estabilizar el sistema, ya que debería cumplirse K2 > 0 y K2 < -(K1+4)/4, es decir, K2 positivo y negativo a la vez. (Házlo como ejercicio)
b) Para aplicar el test de estabilidad de Routh lo primero que necesitamos es la función de transferencia del sistema en lazo cerrado:
$\dfrac {Y\left ( s \right )}{R\left ( s \right )} = \dfrac {C\left ( s \right )G_2\left ( s \right )}{1+C\left ( s \right )G_2\left ( s \right )}$, así que la ecuación característica es $1+C\left ( s \right )G_2\left ( s \right ) = 0$, esto es:
$1+K_2 \dfrac {1}{s(s^2+4s+3+K_1)} = s(s^2+4s+3+K_1)+K_2 \Rightarrow s^3+4s^3+(3+K_1)s+K_2 = 0$.
| s3 | 1 | 3+K1 |
| s2 | 4 | K2 |
| s1 | b | |
| s0 | c |
$b = -\dfrac {1}{4} \begin{vmatrix}1 & 3+K_1 \\ 4 K_2\end{vmatrix} = -\dfrac {1}{4} (K_2-4(3+K_1))$
$c = -\dfrac {1}{b} \begin{vmatrix}4 & K_2 \\ b 0\end{vmatrix} = K_2$
Para que el sistema sea asintóticamene estable no debe haber ningún cambio de signo en la 1ª columna del array de Routh, es decir, debe cumplirse b>0 y c>0. Por lo tanto:
$b>0 \Rightarrow (3+K_1)-K_2/4 > 0 \Rightarrow 3+K_1 > K_2/4 \Rightarrow K_2 < 4(3+K_1)$
$c>0 \Rightarrow K_2 >0$
c) Cumpliendo las condiciones que hemos obtenido en el apartado anterior aseguramos la estabilidad asintótica del sistema en lazo cerrado, sin embargo, también hay que garantizar el cumplimiento de los errores de estado estacionario y limitar el efecto de las perturbaciones sobre la salida.
El error de estado estacionario de posición (velocidad del vehículo), es cero por el echo de que el sistema es te tipo 1 (tiene un polo en s=0 en lazo abierto).
El error de estado estacionario de velocidad (aceleración del vehículo), es:
$e_{ss}=\lim_{s \to 0}sE\left ( s \right )$
$\left . \begin{array}{l}E\left ( s \right )=R\left ( s \right )-Y\left ( s \right ) \\ Y\left ( s \right )=E\left ( s \right )C\left ( s \right )G_2\left ( s \right )\end{array}\right \} \Rightarrow E\left ( s \right ) = \dfrac {R\left ( s \right )}{1+C\left ( s \right )G_2\left ( s \right )}$
Como $e_{ss_{vel}} < 0.5 \Rightarrow \dfrac {3+K_1}{K_2}<0.5 \Rightarrow K_2 > 2(3+K_1)$
Para calcular el efecto de una perturbación sobre la salida debemos obtener la función de transferencia $\dfrac {Y\left ( s \right )}{D\left ( s \right )}$. Si se hace R(s)=0 y se observa el diagrama de bloques resultante, es fácil deducir que:
$\dfrac {Y\left ( s \right )}{D\left ( s \right )} = D\left ( s \right )\dfrac {G_2\left ( s \right )}{1+C\left ( s \right )G_2\left ( s \right )} = \dfrac {1}{s(s^2+4s+3+K_1)+K_2}$
Por lo tanto, siendo D(s) una entrada escalón:
$y(\infty) = \lim_{s \to 0}sY\left ( s \right ) = \lim_{s \to 0} s \dfrac {\dfrac {1}{s}}{s(s^2+4s+3+K_1)+K_2} = \dfrac 1 {K_2} < 0.1 \Rightarrow K_2 >10$
d) Resumiendo, para que el sistema sea asintóticamente estable y se satisfagan los requerimientos del diseño, debe cumplirse:
$\left . \begin{array}{l}1 < K_1 < 3 \\ K_2 < 4(3+K_1) \\ K_2 > 0 \\ K_2 > 2(3+K_1) \\ K_2 > 10\end{array}\right \} \Rightarrow$ Por lo que si se escoge $K_1 =2 \Rightarrow 10 < K_2 < 20$. Por ejemplo, $K_2 = 15$.
e y f) El código que genera todas las simulaciones es:
clc,clear all,close all
% Definición del problema
G=zpk([],[0,-1,-3],1);
K1=2;
H=zpk(0,[],K1);
G2=feedback(G,H);
% Diseño
fprintf('Límites para K2: K2 > %d y K2 < %d\n',max(10,2*(3+K1)),4*(3+K1))
K2=(4*(3+K1)-max(10,2*(3+K1)))/2+max(10,2*(3+K1));
fprintf('Si se escoge K2 en el centro del rango => K2 = %d\n\n',K2)
C=K2;
Glc=feedback(C*G2,1);
% Simulación frente a una entrada escalón
[y1,t]=step(Glc);
plot(t,ones(size(t)),'r--',t,y1)
title('Respuesta a entrada escalón')
xlabel('tiempo (s)'), ylabel('velocidad (m/s)')
error_posicion_teorico=0;
error_posicion_real=1-y1(end);
fprintf('Error de posición:\n\tTeórico: %d\n\tReal: %d\n\n',error_posicion_teorico,error_posicion_real)
% Simulación frente a una entrada rampa
figure
[y2,t]=step(Glc*tf(1,[1,0]),t);
plot(t,t,'r--',t,y2)
title('Respuesta a entrada rampa')
xlabel('tiempo (s)'), ylabel('aceleración (m/s^2)')
error_velocidad_teorico=(3+K1)/K2;
error_velocidad_real=t(end)-y2(end);
fprintf('Error de velocidad:\n\tTeórico: %d\n\tReal: %d\n\n',error_velocidad_teorico,error_velocidad_real)
% Simulación del efecto de la perturbación
figure
Gper=feedback(G2,C);
[y3,t]=step(Gper,t);
plot(t,ones(size(t)),'r--',t,y3)
title('Respuesta a una perturbación escalón')
xlabel('tiempo (s)'), ylabel('velocidad (m/s)')
perturbacion_teorico=1/K2;
perturbacion_real=y3(end);
fprintf('Efecto de una perturbación escalón:\n\tTeórico: %d\n\tReal: %d\n\n',perturbacion_teorico,perturbacion_real)
Los resultados de la consola de MATLAB son:
Límites para K2: K2 > 10 y K2 < 20
Si se escoge K2 en el centro del rango => K2 = 15
Error de posición:
Teórico: 0
Real: 6.026208e-03
Error de velocidad:
Teórico: 3.333333e-01
Real: 3.333037e-01
Efecto de una perturbación escalón:
Teórico: 6.666667e-02
Real: 6.626492e-02
Y las figuras resultantes:
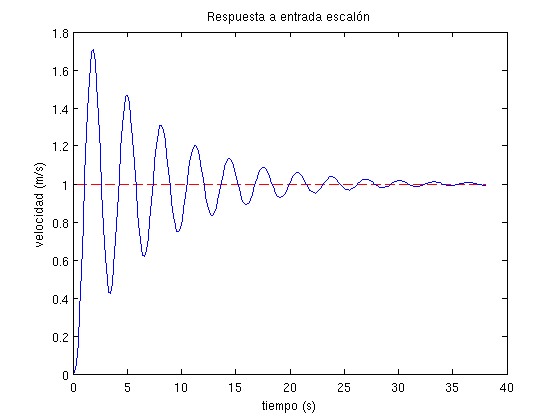
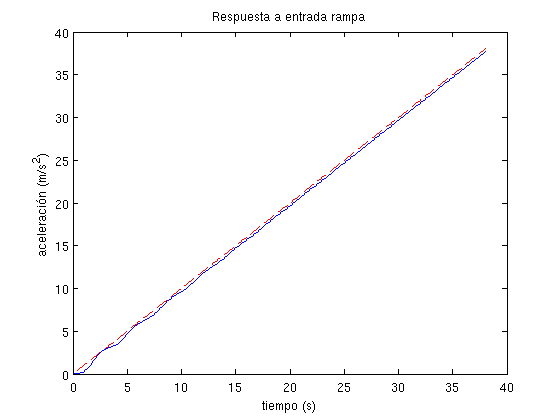
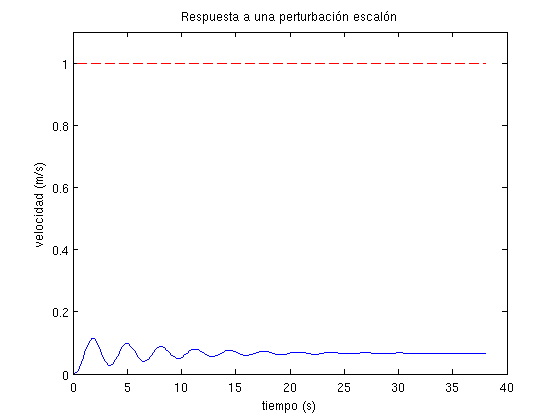
Como puede observarse, tanto en los resultados de la consola como en las representaciones gráficas, se cumplen las condiciones del diseño. Las pequeñas diferencias existentes entre los errores teóricos y reales (según la simulación) son producidos porque el tiempo de simulación evidentemente no es infinito. Conforme se aumenta el tiempo de simulación, los errores teóricos y reales (según la simulación) tienden a converger al mismo valor.
La respuesta dinámica del sistema resultante no es muy buena, ya que presenta muchísima oscilación y un tiempo de asentamiento excesivo. Sería posible escoger un valor más adecuado haciendo un análisis más detallado del sistema. Para ello podemos representar el lugar geométrico de las raíces para el parámetro K2, escogiendo previamente un valor de K1. Si se escoge K1 = 1 y K2 = 10, mejora el tiempo de asentamiento que se sitúa en 12 segundos, y el sobreimpulso, que pasa a ser del 49%, manteniéndose el cumplimiento de los requisitos del problema. Aún así la respuesta del sistema no es del todo satisfactoria. Para obtener una mejor respuesta dinámica sería necesario diseñar un controlador distinto a los propuestos, pero esto forma parte del temario de Automátcia II (es un buen ejercicio si estáis cursado esta asignatura).
 Versión para imprimir
Versión para imprimir- Inicie sesión para enviar comentarios





