Inicie su sesión para modificar los apuntes, usar los foros, etc. Si no es usuario de la web, regístrese.
Resuelto. 2008, diciembre. Ejercicio 2. (3.5 puntos)
Dada la siguiente ecuación diferencial:
$$\dfrac{\partial^3 y(t)}{\partial t^3}+4\dfrac{\partial^2 y(t)}{\partial t^2}+5\dfrac{\partial y(t)}{\partial t}+y(t)+\sin(y(t))-r(t)=0$$
1) Obtener un modelo de estado que represente el sistema no lineal.
2) Obtener un modelo de estado lineal del sistema suponiendo que éste opera en las cercanías del punto y(t)=0
3) Simular durante 20 segundos tanto el sistema lineal como el sistema no lineal, si se toma como punto inicial el origen, para r(t)=1 y r(t)=5, comentando los resultados de la simulación.
Deberá crear una función en un archivo M que describa el sistema no lineal, para poder simularlo mediante la instrucción ode 45
APARTADO 1.
Como la mayor derivada es 3, sabemos que N=3.
\[
\begin{array}{l}
x1 = y(t) \\
\mathop {x1}\limits^ \bullet = \mathop y\limits^ \bullet (t) = x2 \\
\mathop x\limits^ \bullet 2 = \mathop y\limits^{ \bullet \bullet } (t) = x3 \\
\mathop x\limits^ \bullet 3 = \\
\end{array}
\]
Despejamos de la ecuación \[\mathop x\limits^ \bullet 3\] pero primero reemplazamos los nombres
\[
\begin{array}{l}
\mathop x\limits^ \bullet 3 + 4x3 + 5x2 + x1 + sen(x1) - r(t) = 0 \\
\mathop x\limits^ \bullet 3 = - 4x3 - 5x2 - x1 - sen(x1) + r(t) \\
\end{array}
\]
Por tanto el modelo de estado seria:
\[
\begin{array}{l}
\mathop {x1}\limits^ \bullet = x2 \\
\mathop x\limits^ \bullet 2 = x3 \\
\mathop x\limits^ \bullet 3 = - 4x3 - 5x2 - x1 - sen(x1) + r(t) \\
\end{array}
\]
Y la sálida será:
\[
y(t) = x1
\]
APARTADO 2.
\[
\frac{{\partial ^3 y(t)}}{{\partial t^3 }} + 4\frac{{\partial ^2 y(t)}}{{\partial t^2 }} + 5\frac{{\partial y(t)}}{{\partial t}} + y(t) + sen(y(t)) - r(t) = 0
\]
Como \[
sen(y(t))
\]
es no lineal, lo linealizamos por medio del polinomio de Taylor.
\[
\begin{array}{l}
sen(y(t)) \cong sen(y_0 (t)) + \left. {\frac{{\partial sen(y(t))}}{{\partial t}}} \right|_{x_0 } *\frac{{(y - y_0 )}}{1} + ... \\
sen(y(t)) \cong sen(y_0 (t)) + \cos y(t)*(y - y_0 ) + ... \\
\end{array}
\]
Estudiamos el caso para \[
y_0 (t) = 0
\]
Que reemplazandolo será
\[
\begin{array}{l}
sen(y(t)) \cong 0 + 1(y - 0) \\
sen(y(t)) \cong y \\
\end{array}
\]
Por tanto la ecuación quedaría
\[
\begin{array}{l}
\frac{{\partial ^3 y(t)}}{{\partial t^3 }} + 4\frac{{\partial ^2 y(t)}}{{\partial t^2 }} + 5\frac{{\partial y(t)}}{{\partial t}} + y(t) + y(t) - r(t) = 0 \\
\frac{{\partial ^3 y(t)}}{{\partial t^3 }} + 4\frac{{\partial ^2 y(t)}}{{\partial t^2 }} + 5\frac{{\partial y(t)}}{{\partial t}} + 2y(t) - r(t) = 0 \\
\end{array}
\]
Ahora convertimos la ecuación en modelo de estados
Como la mayor derivada es 3, sabemos que N=3.
\[
\begin{array}{l}
x1 = y(t) \\
\mathop {x1}\limits^ \bullet = \mathop y\limits^ \bullet (t) = x2 \\
\mathop x\limits^ \bullet 2 = \mathop y\limits^{ \bullet \bullet } (t) = x3 \\
\end{array}
\]
Despejamos de la ecuación \[\mathop x\limits^ \bullet 3\] pero primero reemplazamos los nombres
\[
\begin{array}{l}
\mathop x\limits^ \bullet 3 + 4x3 + 5x2 + 2x1 - r(t) = 0 \\
\mathop x\limits^ \bullet 3 = - 4x3 - 5x2 - 2x1 + r(t) \\
\end{array}
\]
Por tanto el modelo de estado seria:
\[
\begin{array}{l}
\mathop {x1}\limits^ \bullet = x2 \\
\mathop x\limits^ \bullet 2 = x3 \\
\mathop x\limits^ \bullet 3 = - 4x3 - 5x2 - 2x1 + r(t) \\
\end{array}
\]
Y la sálida será:
\[
y(t) = x1
\]
Representado de forma matricial seria.
\[
\left[ {\begin{array}{*{20}c}
{\mathop {x1}\limits^ \bullet } \\
{\mathop {x2}\limits^ \bullet } \\
{\mathop {x3}\limits^ \bullet } \\
\end{array}} \right] = \left[ {\begin{array}{*{20}c}
0 & 1 & 0 \\
0 & 0 & 1 \\
{ - 2} & { - 5} & { - 4} \\
\end{array}} \right]*\left[ {\begin{array}{*{20}c}
{\mathop {x1}\limits^{} } \\
{\mathop {x2}\limits^{} } \\
{\mathop {x3}\limits^{} } \\
\end{array}} \right] + \left[ {\begin{array}{*{20}c}
0 \\
0 \\
1 \\
\end{array}} \right]*r(t)
\]
Y la sálida será:
\[
\left[ {y(t)} \right] = \left[ {\begin{array}{*{20}c}
1 & 0 & 0 \\
\end{array}} \right]*\left[ {\begin{array}{*{20}c}
{x1} \\
{x2} \\
{x3} \\
\end{array}} \right] + \left[ 0 \right]*r(t)
\]
APARTADO 3.
Primero lo haremos para el sistema no lineal.
- Creamos primero la función.
function dx=nolineal(t,x)
R=1; Como nos dice, que simularlo con R=1 y R=5, aqui en la otra simulación simplemente lo cambiamos por 5
dx=zeros(3,1);
dx(1)=x(2);
dx(2)=x(3);
dx(3)=-x(1)-5*x(2)-4*x(3)+R-sin(x(1));
Nota: Al guardar la función, ponerle el mismo nombre que le hemos puesto a la función, en este caso "nolineal"
- Ahora creamos el archivo que va a ejecutar la función.
x0=[0;0;0];
tf=20;
[t,x]=ode45(@nolineal,[0,tf],x0);
plot(t,x),grid
xlabel('tiempos');
ylabel('variables de estado')
legend ('x_1','x_2','x_3')
Y la gráfica que nos devuelve el sistema es
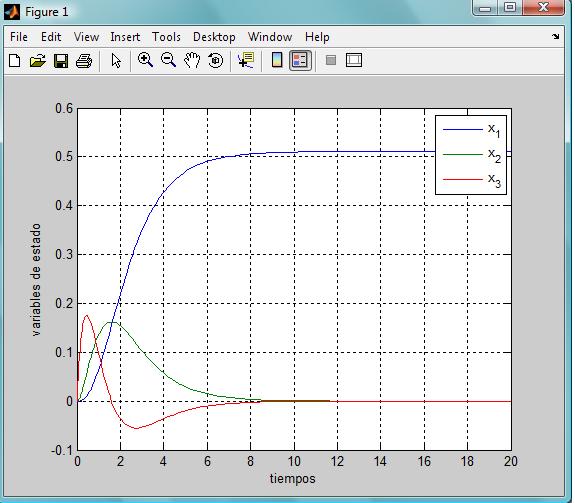
Ahora lo haremos para el sistema lineal
clc, clear all, close all
A=[0,1,0;0,0,1;-2,-5,-4];
B=[0;0;1];
C=[1,0,0];
D=[0];
Sistema1=ss(A,B,C,D); %Coje las 4 matrices y lo convierte en un sistema lineal
step(Sistema1,20)
Y la gráfica que nos devuelve el sistema es
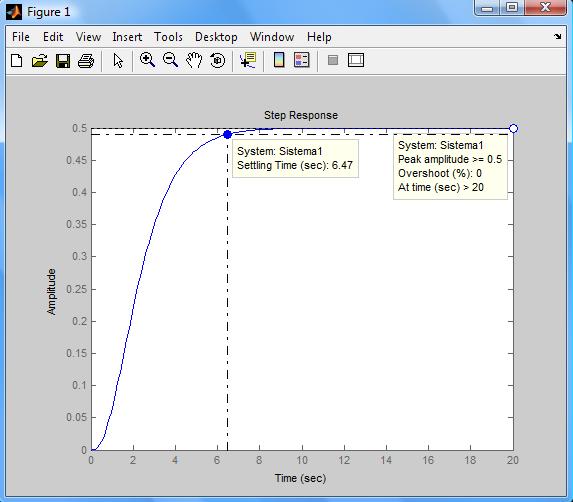
 Versión para imprimir
Versión para imprimir- Inicie sesión para enviar comentarios





