Versión para imprimir

El sistema de la figura está formado por dos depósitos interconectados donde $q_e(t)$ es el caudal entrante en cada depósito y, para cada uno de los depósitos, $h_1(t)$ y $h_2(t)$ es la altura de líquido, $q_1(t)$ y $q_2(t)$ el caudal de salida, y $A_1$ y $A_2$ el área transversal. La dinámica del sistema puede ser representada mediante el siguiente conjunto de ecuaciones:

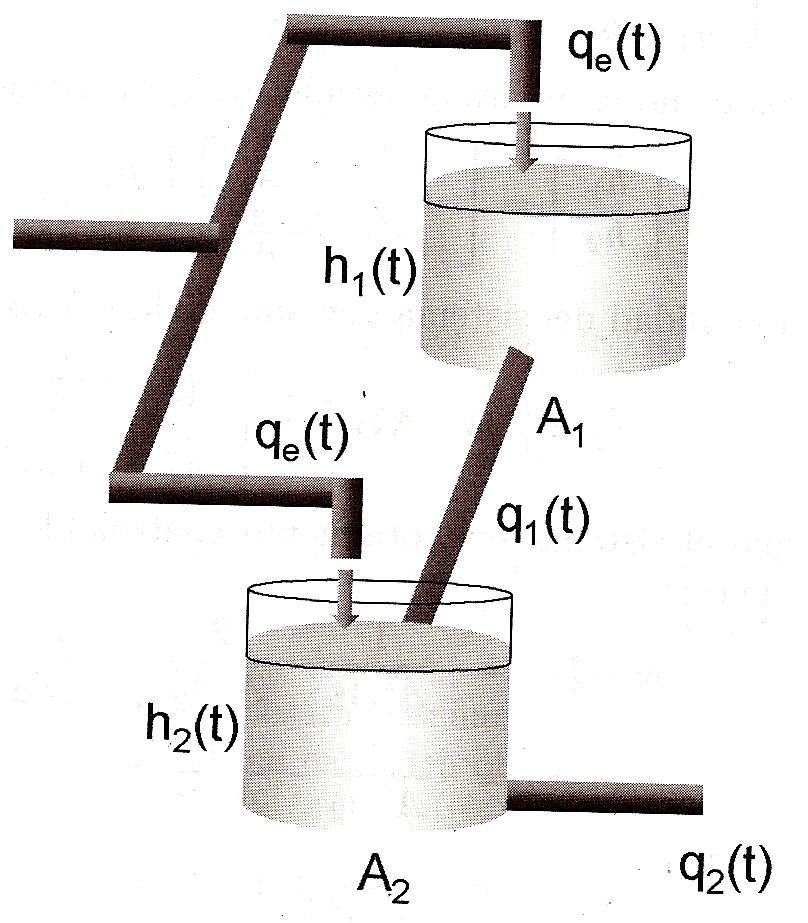$A_1 \dot{h}_1(t)=q_e(t)-q_1(t)$ $A_2 \dot{h}_2(t) = q_e(t)+q_1(t)-q_2(t)$ $q_1(t)=h_1(t)-h_2(t)$ $q_2(t)=h_2(t)$ $A_1=2 m^2$ $A_2 = 1 m^2$

Se solicita:

1. Identifique las variables de entrada, salida e internas del sistema, determine el número de variables de estado necesarias para representar el modelo de estado del sistema y obtenga un modelo de estado de tiempo continuo para el mismo.
2. Escoja uno de los siguientes periodos de muestreo para el sistema según cuál resulte más adecuado. Justifique su elección.

   a) T = 0.1s

   b) T = 0.3s

   c) T = 0.8s

3. Discretice el modelo de estado empleando dicho periodo de muestreo.
4. Simule el modelo discretizado y represente la salida de caudal del segundo depósito, $q_2(t)$, para una entrada $q_e(t) = 1 m^3/s$.
5. Comente los resultados obtenidos. ¿Se puede decir que el sistema es estable? ¿Por qué?

Recuerde:

$\dfrac{\text{d}x(t)}{\text{d}t} \simeq \dfrac{x(k+1) - x(k)}{T}$, siendo T el periodo de muestreo y el tiempo discreto.

$t_s \approx 5 \tau$, siendo $t_s$ el tiempo de establecimiento y $\tau$ la constante de tiempo del sistema.

Solución:

1.) Las variables de entrada del sistema, se aprecian claramente en el gráfico que muestra el sistema a analizar, determinando que la entrada al sistema es qe(t), debido a que son las únicas tuberías que pueden incorporar fluido a los depósitos A1 y A2. Del mismo modo, se determina que la variable de salida será q2(t), ya que es la única variable que sale del sistema al exterior (fuera de lo representado en el esquema).
En este caso, como podemos apreciar, los elementos capaces de almacenar fluido en el sistema serán los depósitos, siendo pues las variables el volumen que habrá que hay en ellos, es decir, h1(t) y h2(t), de modo que podemos modelar el sistema.

   Antes de modelar, reducimos las ecuaciones del mismo, obteniendo 2 ecuaciones, debido a que el sistema nos presenta 2 elementos almacenadores de 1er orden.

${A_1}\cdot{{\dot h}_1}\left( t \right) = {q_e}\left( t \right) - {h_1}\left( t \right) + {h_2}\left( t \right)$

${A_2}\cdot{{\dot h}_2}\left( t \right) = {q_e}\left( t \right) + {h_1}\left( t \right) - 2{h_2}\left( t \right)$

Ahora, hacemos la siguiente operación:

${x_1} = {h_1}\left( t \right)\mathop \to \limits^{\frac{{dx}}{{dt}}} {{\dot X}_1} = \frac{{d{h_1}(t)}}{{dt}} = {{\dot h}_1}(t)$

${x_2} = {h_2}\left( t \right)\mathop \to \limits^{\frac{{dx}}{{dt}}} {{\dot X}_2} = \frac{{d{h_2}(t)}}{{dt}} = {{\dot h}_2}(t)$

El sistema quedará entonces del siguiente modo:

${{\dot X}_1}\left( t \right) = \frac{{ - {x_1}\left( t \right)}}{{{A_1}}} + \frac{{{x_2}\left( t \right)}}{{{A_1}}} + \frac{{{q_e}\left( t \right)}}{{{A_1}}}$

${{\dot X}_2}\left( t \right) = \frac{{{x_1}\left( t \right)}}{{{A_2}}} - \frac{{2{x_2}\left( t \right)}}{{{A_2}}} + \frac{{{q_e}\left( t \right)}}{{{A_2}}}$

    Al ser un sistema lineal, se puede poner de forma matricial, siendo este el que usaremos para realizar las simulaciones pertinentes.

$\left[ {\begin{array}{*{20}{c}}
{{{\dot X}_1}}\\
{{{\dot X}_2}}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{-\frac{1}{{{A_1}}}}&{\frac{1}{{{A_1}}}}\\
{\frac{1}{{{A_2}}}}&{\frac{{ - 2}}{{{A_2}}}}
\end{array}} \right]\cdot\left[ {\begin{array}{*{20}{c}}
{{x_1}}\\
{{x_2}}
\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}
{\frac{1}{{{A_1}}}}\\
{\frac{1}{{{A_2}}}}
\end{array}} \right]\cdot{q_e}(t)$

La ecuación de salida, al ser q2(t)=h2(t), será:

$y = \left[ {\begin{array}{*{20}{c}}
0&1
\end{array}} \right]\cdot\left[ {\begin{array}{*{20}{c}}
{{x_1}}\\
{{x_2}}
\end{array}} \right] + 0\cdot{q_e}(t)$

2.) Para determinar correctamente el periodo del modelo discreto, simularemos el modelo no discreto en matlab, obteniendo así una función de la salida, en este caso, correspondiente a q2(t), para lo cual emplearemos el siguiente código de matlab:

clc, clear all, close all
%---------------------------------------------------------------------
%Simulación del sistema no discretizado:
%---------------------------------------------------------------------
%Constantes del sistema:
A1=2; %m^2
A2=1; %m^2

%Matrices del modelo:
A=[-1/A1, 1/A1; 1/A2, -2/A2];
B=[1/A1; 1/A2];
C=[0,1];
D=0;

%Declaración del modelo y simulación:
Sistema=ss(A,B,C,D);
[y,t,x]=step(Sistema);
figure
plot(t,y) %Salida del sistema
title('Modelo no discretizado'),xlabel('tiempo')
ylabel('caudal'),legend('y')

Simulando, obtenemos la siguiente gráfica, donde marcamos Tau, siendo su valor el valor que toma la gráfica cuando ha llegado al 63% de su valor total:

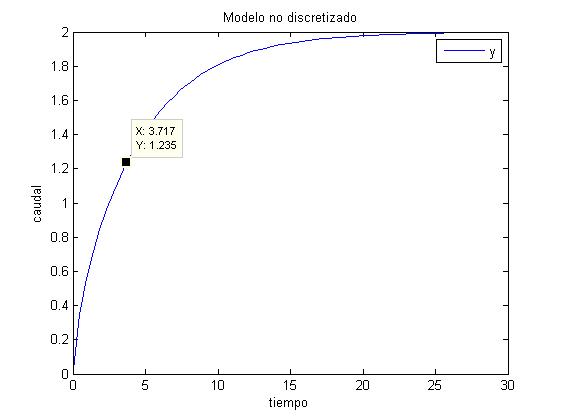
Como se aprecia en la gráfica anterior, el valor de Tau, es 3.717, de modo que aplicamos la siguiente fórmula para obtener el periodo:

$\frac{{10}}{{Tau}} \le \frac{1}{T} \le \frac{{20}}{{Tau}}$

Aplicando la ecuación, obtendremos que:

$\frac{{Tau}}{{10}} \le T \le \frac{{Tau}}{{20}}\mathop \Rightarrow \limits^{Tau = 3.717} 0.18585 \le T \le 0.3717$

Al tener que estar T comprendido entre esos dos valores, elegimos el único de los 3 dados por el problema que cumple la ecuación, de modo que T=0.3 (opción b) para todo lo que resta de problema.

3.) Antes de poner el modelo discretizado, habrá que obtener la forma de discretizar el sistema, para lo cual, utilizaremos la definición de derivada dada en el enunciado:

$\dfrac{\text{d}x(t)}{\text{d}t} \simeq \dfrac{x(k+1) - x(k)}{T}$

Aplicandola a un sistema general, para llegar a la solución particular de nuestro sistema, siendo:

$\frac{{\vec x\left( {k + 1} \right) - \vec x\left( k \right)}}{T} = A\cdot\vec x\left( k \right) + B\cdot\vec u\left( k \right)$

$\vec x(k + 1) - \vec x(k) = T\cdot A\cdot\vec x(k) + T\cdot B\cdot\vec u(k)$

$\vec x\left( {k + 1} \right) = [T\cdot A + I]\cdot\vec x\left( k \right) + T\cdot B\cdot\vec u\left( k \right)$

Nuestro sistema discretizado tendría la siguiente forma:

$\left[ {\begin{array}{*{20}{c}}
{{x_1}(k + 1)}\\
{{x_2}(k + 1)}
\end{array}} \right] = \left[ {T*\left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{\frac{{ - 1}}{{{A_1}}}}&{\frac{1}{{{A_1}}}}\\
{\frac{1}{{{A_2}}}}&{\frac{{ - 2}}{{{A_2}}}}
\end{array}}
\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}
1&0\\
0&1
\end{array}} \right]} \right]\cdot\left[ {\begin{array}{*{20}{c}}
{{x_1}}\\
{\begin{array}{*{20}{c}}
{{x_2}}
\end{array}}
\end{array}} \right] + T*\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{{A_1}}}}\\
{\frac{1}{{{A_2}}}}
\end{array}} \right]\cdot{q_e}\left( k \right)$

$\left[ {\begin{array}{*{20}{c}}
{{x_1}(k + 1)}\\
{{x_2}(k + 1)}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{\frac{{ - T}}{{{A_1}}} + 1}&{\frac{T}{{{A_1}}}}\\
{\frac{T}{{{A_2}}}}&{\frac{{ - 2T}}{{{A_2}}} + 1}
\end{array}}
\end{array}} \right]\cdot\left[ {\begin{array}{*{20}{c}}
{{x_1}}\\
{\begin{array}{*{20}{c}}
{{x_2}}
\end{array}}
\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}
{\frac{T}{{{A_1}}}}\\
{\frac{T}{{{A_2}}}}
\end{array}} \right]\cdot{q_e}\left( k \right)$

Quedando de forma numérica:

$\left[ {\begin{array}{*{20}{c}}
{{x_1}(k + 1)}\\
{{x_2}(k + 1)}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{0.85}&{0.15}\\
{0.3}&{0.4}
\end{array}}
\end{array}} \right]\cdot\left[ {\begin{array}{*{20}{c}}
{{x_1}}\\
{\begin{array}{*{20}{c}}
{{x_2}}
\end{array}}
\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}
{0.15}\\
{0.3}
\end{array}} \right]\cdot{q_e}\left( k \right)$

Del mismo obtenemos salida del sistema, siendo para este caso:

$y = \left[ {\begin{array}{*{20}{c}}
0&1
\end{array}} \right]\cdot\left[ {\begin{array}{*{20}{c}}
{{x_1}(k)}\\
{{x_2}(k)}
\end{array}} \right] + 0\cdot{q_e}(k)$

4.) Simularemos el sistema discretizado, siendo la salida a representar q2(t) discretizado, siendo el código de matlab el siguiente:

clc, clear all, close all
%Constantes del sistema:
A1=2; %m^2
A2=1; %m^2

%Matrices del modelo:
A=[-1/A1, 1/A1; 1/A2, -2/A2];
B=[1/A1; 1/A2];
C=[0,1];
D=0;

%Periodo (T)
T=0.3; %segundos
%Matrices del sistema
Ak=[T*A+eye(2,2)];
Bk=T*B;
Ck=C;
Dk=D;

%Simulación del sistema
Sistema_discreto=ss(Ak,Bk,Ck,Dk,T);
[yk,tk,xk]=step(Sistema_discreto);
figure
plot(tk,yk) %Salida del sistema
title('Modelo DISCRETIZADO'), xlabel('tiempo'),ylabel('caudal'),legend('y')

La gráfica obtenida es la siguiente:

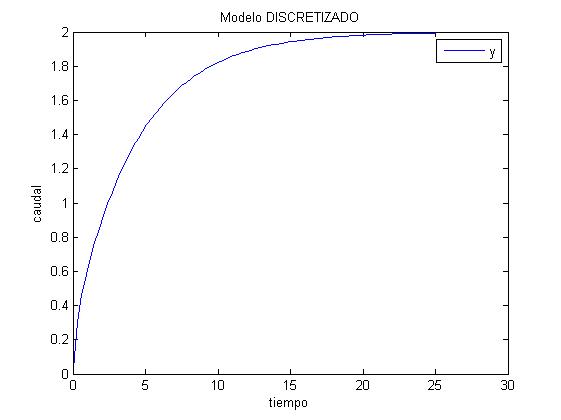
5.) Cuando se le aplica un caudal de entrada, el sistema va llenando los depósitos hasta que la salida consigue un caudal estable.
Al ser un sistema que trabaja en una región lineal, podemos asegurar la estabilidad hallando los autovalores de la matriz de estados del sistema (matriz A), lo cual se realiza en matlab gracias al siguiente código, el cual, irá al final del código anterior:

%Cálculo de estabilidad

%primero, obtenemos los autovalores de la matriz A:
autovalores=eig(A); %obtendremos 2 autovalores al ser una matriz 2x2

%creamos el programa que imprima en pantalla como es el sistema:
if isreal(autovalores(1)) && (autovalores(1)<0 && autovalores(2)<0)
fprintf('Sistema estable, con autovalores reales\n')
elseif ~isreal(autovalores(1))&& (real(autovalores(1))<0 && real(autovalores(2))<0)
fprintf('Sistema estable, con autovalores complejos conjugados\n')
else
fprintf('sistema inestable\n')
end

%Con esto queda demostrada la estabilidad del sistema, y finaliza el código
%del ejercicio.

Para el ejercicio, una vez simulado, hemos obtenido el siguiente resultado: “Sistema estable, con autovalores reales”, ya que los autovalores de la matriz son -0.2192 y
-0.2808, lo cual nos dice también de forma teórica que la estabilidad del sistema está garantizada.

Nota: De encontrar algún error en los cálculos, desarrollo, o simulaciones, puede corregirlos directamente (esto es un wiki) o mandar un correo a vfernandez.fernandez AT alu.uhu.es para corregirlo lo mas rápido posible.

Simulacines y cálculos realizados por:

Victor Fernández Fernández

Carlos Javier Marín Mallo

Cristóbal Domínguez Blanco