A. Javier Barragán Piña

Versión para imprimir

Dada la siguiente ecuación diferencial:

1) Obtener un modelo de estado que represente el sistema no lineal.

2) Obtener un modelo de estado lineal del sistema suponiendo que éste opera en las cercanías del punto y(t)=0

3) Simular durante 20 segundos tanto el sistema lineal como el sistema no lineal, si  se toma como punto inicial el origen, para r(t)=1 y r(t)=5, comentando los resultados de la simulación.

Deberá crear una función en un archivo M que describa el sistema no lineal, para poder simularlo mediante la instrucción ode 45

APARTADO 1.

Como la mayor derivada es 3, sabemos que N=3.

Por tanto el modelo de estado seria:

APARTADO 2.

Ahora convertimos la ecuación en modelo de estados

Como la mayor derivada es 3, sabemos que N=3.

Por tanto el modelo de estado seria:

Representado de forma matricial seria.

APARTADO 3.

Primero lo haremos para el sistema no lineal.

• Creamos primero la función.

function dx=nolineal(t,x)
dx=zeros(3,1);
dx(1)=x(2);
dx(2)=x(3);
dx(3)=-x(1)-5*x(2)-4*x(3)+1-sin(x(1));

Nota: Al guardar la función, ponerle el mismo nombre que le hemos puesto a la función, en este caso "nolineal"

• Ahora creamos el archivo que va a ejecutar la función.

x0=[0;0;0];
tf=20;
[t,x]=ode45(@nolineal,[0,tf],x0);
plot(t,x),grid
xlabel('tiempos');
ylabel('variables de estado')
legend ('x_1','x_2','x_3')

Y la gráfica que nos devuelve la figura es

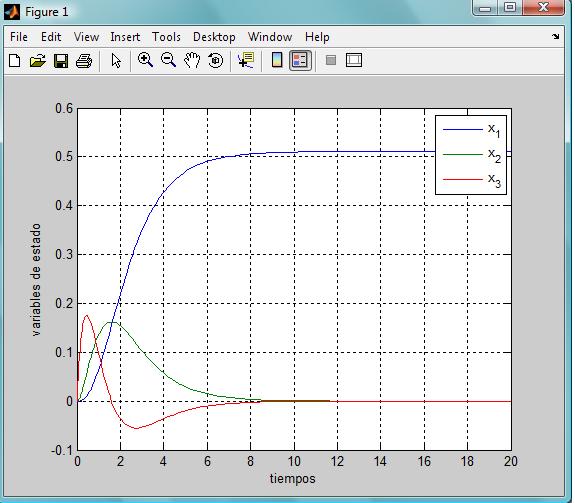
Ahora lo haremos para el sistema lineal