A. Javier Barragán Piña

Versión para imprimir

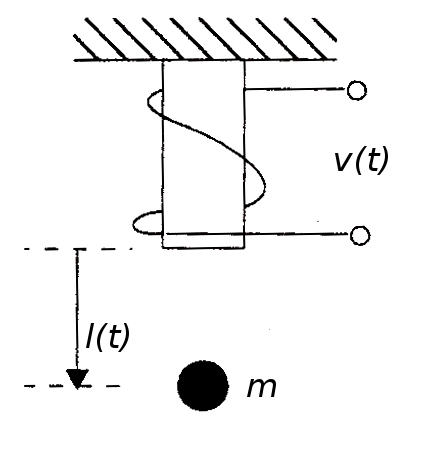
En la figura se puede observar el esquema simplificado de un sistema de levitación magnética similar al utilizado por los trenes de última tecnología. El campo magnético generado en la bobina a partir de la tensión de entrada $v(t)$, provoca la elevación de la bola de metal de masa m, de forma que controlando adecuadamente la tensión de entrada puede mantenerse suspendida la masa a una distancia $l(t)$ determinada. Dado el conjunto de ecuaciones que gobierna la dinámica del sistema, se desea estudiar el comportamiento del mismo, para lo cual se solicita:

$m \dfrac{\text{d}^2 l(t)}{\text{d} t^2} = m g - \dfrac{i(t)^2}{l(t)}$ $v(t) = R i(t) + L \dfrac{\text{d}i(t)}{\text{d}t}$ Masa → $m = 0.01 kg$ Inductancia del bobinado → $L = 0.1 H$ Resistencia del bobinado → $R = 10 \Omega$ Aceleración de la gravedad → $g = 9.8 m/s ^2$ Distancia de la masa al electroimán → $l(t) > 0$  (en mm)

1. Utilice las ecuaciones anteriores para obtener un modelo de estado del sistema.
2. Determine el estado de equilibrio del sistema para $v(t) = v_{eq} =10 V$.
3. Linealice el sistema en el estado de equilibrio obtenido. ¿Es este estado de equilibrio estable? Argumente su respuesta. Recuerde que:$$\dot{\mathbf{x}} \simeq \mathbf{A} (\mathbf{x} - \mathbf{x}_{eq}) + \mathbf{B} (\mathbf{u} - \mathbf{u}_{eq})$$

   $${\small \mathbf{A} = \left.\left(\begin{array}{cccc} \dfrac{\partial f_1}{\partial x_1} & \dfrac{\partial f_1}{\partial x_2} & \cdots & \dfrac{\partial f_1}{\partial x_n}\\ \dfrac{\partial f_2}{\partial x_1} & \dfrac{\partial f_2}{\partial x_2} & \cdots & \dfrac{\partial f_2}{\partial x_n}\\ \cdots & \cdots & \ddots & \cdots\\ \dfrac{\partial f_n}{\partial x_1} & \dfrac{\partial f_n}{\partial x_2} & \cdots & \dfrac{\partial f_n}{\partial x_n}\\ \end{array}\right)\right|_{ \begin{array}{l} \mathbf{x}=\mathbf{x}_{eq}\\ \mathbf{u}=\mathbf{u}_{eq} \end{array} } }$$

   $${\small \mathbf{B} = \left.\left(\begin{array}{cccc} \dfrac{\partial f_1}{\partial u_1} & \dfrac{\partial f_1}{\partial u_2} & \cdots & \dfrac{\partial f_1}{\partial u_m}\\ \dfrac{\partial f_2}{\partial u_1} & \dfrac{\partial f_2}{\partial u_2} & \cdots & \dfrac{\partial f_2}{\partial u_m}\\ \cdots & \cdots & \ddots & \cdots\\ \dfrac{\partial f_n}{\partial u_1} & \dfrac{\partial f_n}{\partial u_2} & \cdots & \dfrac{\partial f_n}{\partial u_m}\\ \end{array}\right)\right|_{ \begin{array}{l} \mathbf{x}=\mathbf{x}_{eq}\\ \mathbf{u}=\mathbf{u}_{eq} \end{array} } }$$

4. Simule el comportamiento del sistema linealizado durante 2 segundos partiendo de un punto cercano al estado de equilibrio. Represente cada variable de estado en una gráfica. Comente e interprete los resultados obtenidos en la simulación.
5. Simule el comportamiento del sistema no lineal durante 2 segundos partiendo del mimo punto anterior. Represente cada variable de estado en una gráfica. Comente e interprete los resultados de la simulación.